- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на неравенство треугольника
Содержание
- 2. Неравенство треугольника Длина любой стороны треугольника
- 3. Следствия из неравенства треугольникаРавенство | AC |
- 4. Задача 1: a, b, c – стороны треугольника,
- 5. Задача 1РЕШЕНИЕ1) Из неравенства треугольника c <
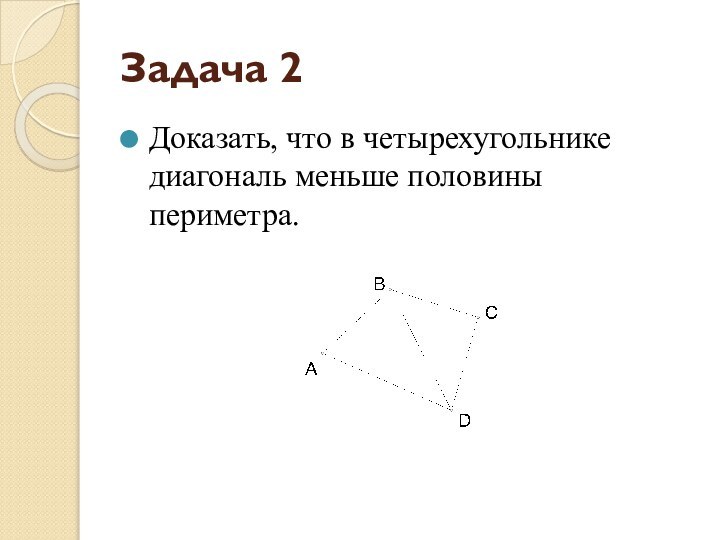
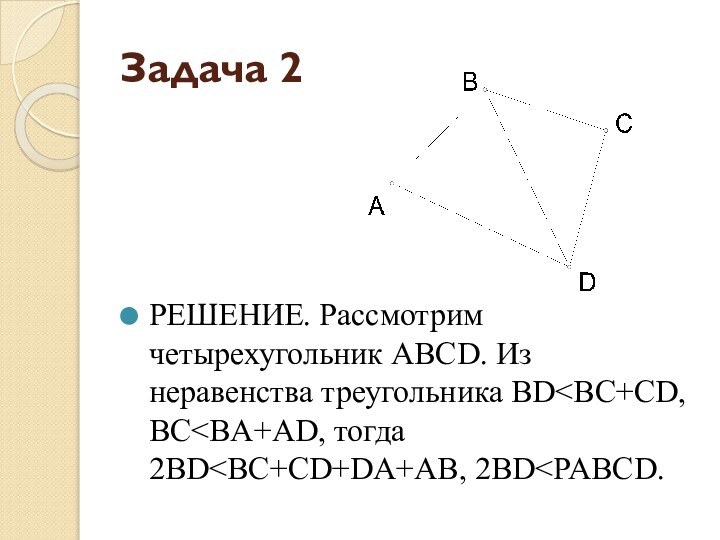
- 6. Задача 2Доказать, что в четырехугольнике диагональ меньше половины периметра.
- 7. Задача 2РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Из неравенства треугольника BD
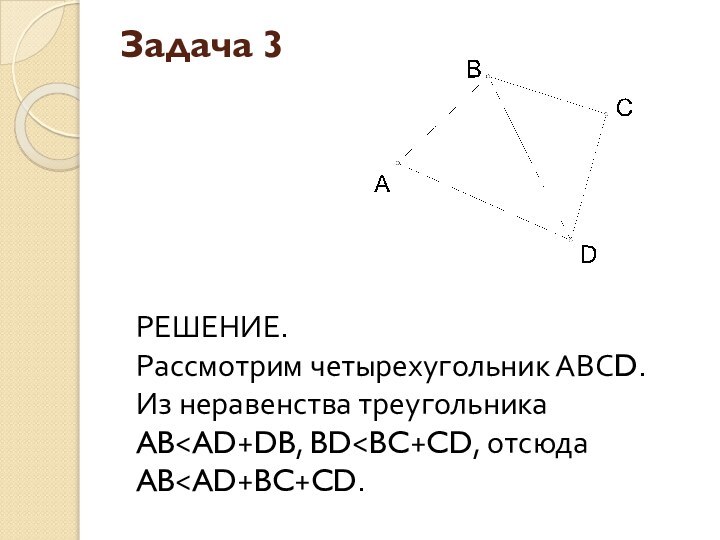
- 8. Задача 3: Доказать, что в четырехугольнике любая сторона меньше суммы остальных.
- 9. Задача 3 РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Из неравенства треугольника AB
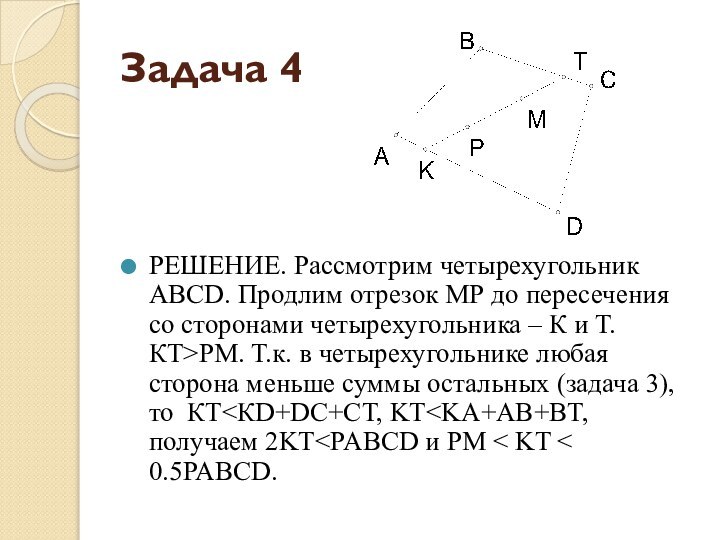
- 10. Задача 4М и Р – точки внутри четырехугольника.
- 11. Задача 4РЕШЕНИЕ. Рассмотрим четырехугольник АВСD. Продлим отрезок
- 12. Задача 5Есть 7 прутьев длиннее 9 см, но
- 13. Скачать презентацию
- 14. Похожие презентации
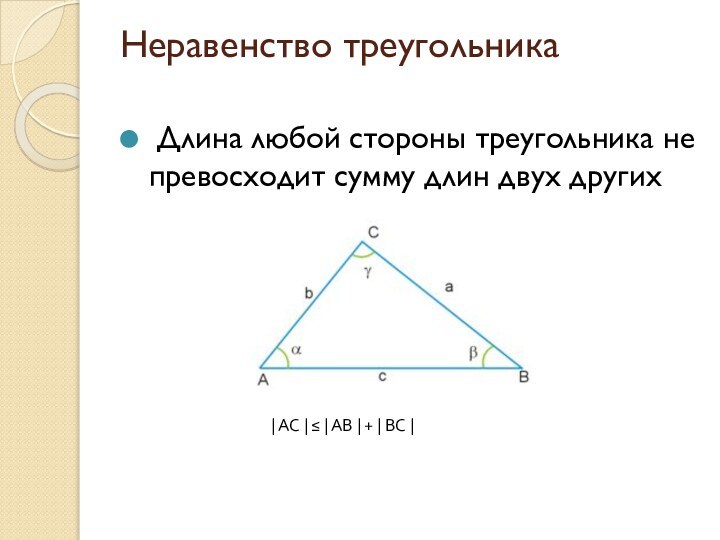
Неравенство треугольника Длина любой стороны треугольника не превосходит сумму длин двух других| AC | ≤ | AB | + | BC |





Слайд 2
Неравенство треугольника
Длина любой стороны треугольника не превосходит
сумму длин двух других
| + | BC |
Слайд 3
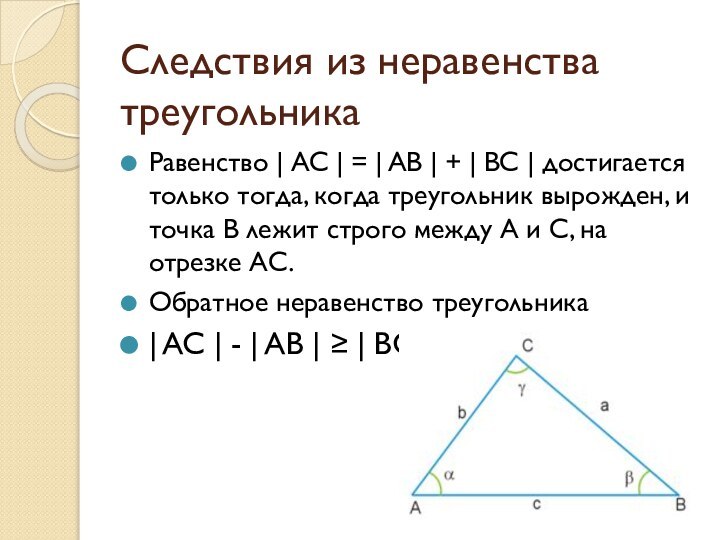
Следствия из неравенства треугольника
Равенство | AC | =
| AB | + | BC | достигается только
тогда, когда треугольник вырожден, и точка B лежит строго между A и C, на отрезке АС.Обратное неравенство треугольника
| AC | - | AB | ≥ | BC |
Слайд 4
Задача 1:
a, b, c – стороны треугольника, c –
целое число. Найти c.
1) а=8, b=6, с>12
2) a = 3,17, b = 0,75
Слайд 5
Задача 1
РЕШЕНИЕ
1) Из неравенства треугольника c < a+b,
с< 8+6, с12. Т.к. с -
целое число, оно равно 13.2) Из неравенства треугольника c < a+b, с<3,17+0,75, с< 3,92; но из обратного неравенства треугольника c>a-b, т.е. с> 3,17-0,75, c>2,42. Т.к. с - целое число, оно равно 3.





























