Презентация на тему Задачи на построение с помощью циркуля и линейки

мы познакомились с задачами на построение. В учебниках предложен

один способ построения для каждой классической задачи.
Я попыталась оформить все задачи в электронном виде и для одной из задач провести исследование.

построение, которые можно решить только с помощью двух инструментов:

циркуля и линейки без масштабных делений.

Линейка позволяет провести произвольную
прямую, а также построить прямую, проходящую
через две данные точки; с помощью циркуля
можно провести окружность произвольного
радиуса, а также окружность с центром в
данной точке и радиусом, равным данному
отрезку.

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

ПОСТРОЕНИЕ
3. ДОКАЗАТЕЛЬСТВО
4. ИССЛЕДОВАНИЕ
В том случае, когда при построении получаются

равные фигуры, будем считать, что задача имеет единственное решение.

центром в точке О и

радиусом г

∩ - знак пересечения

{ } - в скобках указано множество точек пересечения

∈ - знак принадлежности

⊥ - знак перпендикулярности

: - заменяет слова ”такой что”

отрезок, равный данному
Дано:
Луч h, О- начало
PQ-отрезок
Построить:
A∈h
OA=PQ

h

A
Построение:
1. окр(О;PQ)
2. h∩окр(O;PQ)=

{A}

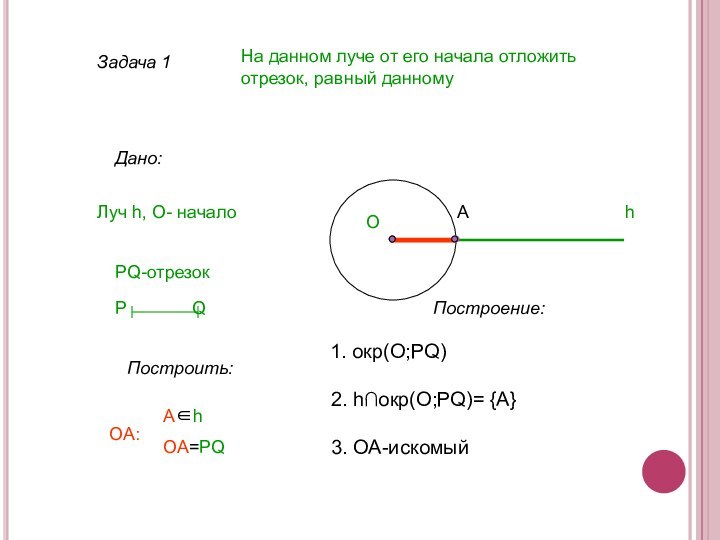
3. OA-искомый

P Q

OA:

O

окр(А;АВ)∩окр(В;ВА)= {P;Q}
4. PQ-прямая
P
Q
5. PQ∩AB={O}
О
6. O- искомая точка

B
O

как 1) AP=BP=г

2) AQ=BQ=г
3) PQ-общая
Следовательно, ∠1=∠2

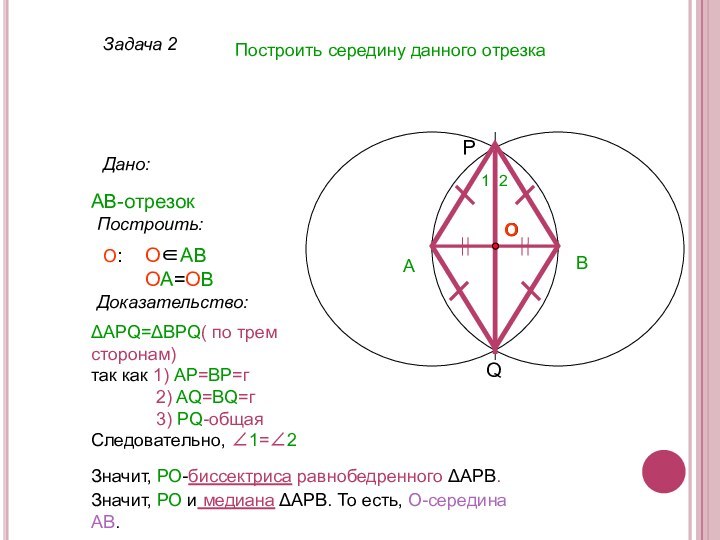
Значит, РО-биссектриса равнобедренного ΔАРВ.

1

2

Значит, РО и медиана ΔАРВ. То есть, О-середина АВ.

которой меньше данного отрезка)
Дано:
АВ-отрезок
А
Построить:
О∈АВ
ОА=ОВ
О:
Построение:


1. окр(А ;АF)
2. окр(В;ВM)
3. окр(А;АF)∩окр(В;ВM{P;Q}
4. PQ-прямая
P
Q
5.

PQ∩AB={O}

О

6. O- искомая точка

B

O

М

F

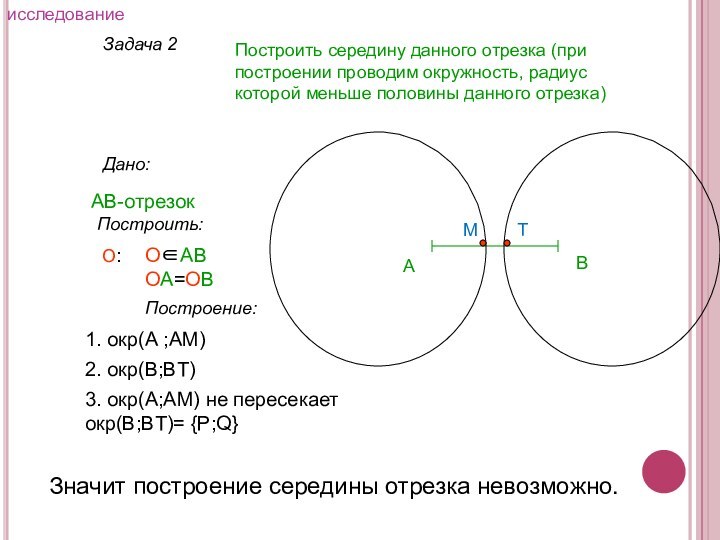
исследование

окружность, радиус которой меньше половины данного отрезка)
Дано:
АВ-отрезок
А
Построить:
О∈АВ
ОА=ОВ
О:
Построение:


1. окр(А ;АM)
2.

окр(В;ВT)

3. окр(А;АM) не пересекает окр(В;ВT)= {P;Q}

B

М

T

исследование

Значит построение середины отрезка невозможно.

перпендикулярную к данной прямой
Дано:
прямая а
а
точка M
Построить:
m:
M∈m
m ⊥a
точка

М принадлежит прямой а

М

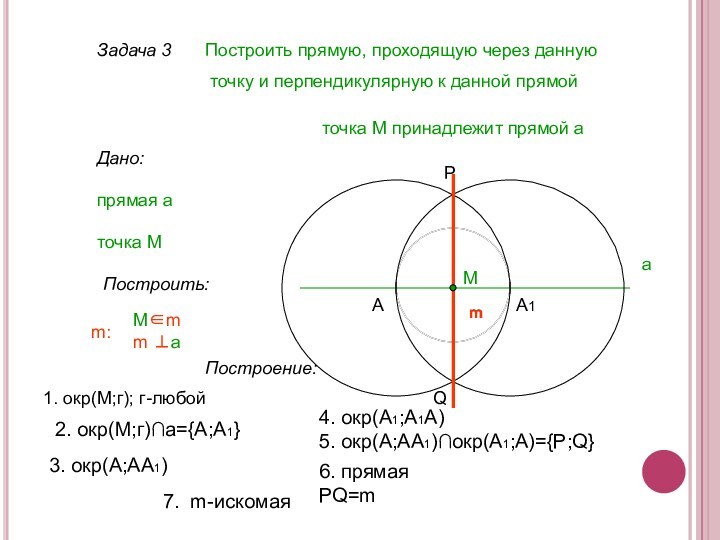
Построение:

1. окр(М;г); г-любой

A

A1

2. окр(М;г)∩а={А;А1}

3. окр(А;АА1)

4. окр(А1;A1A)

5. окр(А;АА1)∩окр(А1;А)={P;Q}

P

Q

6. прямая PQ=m

7. m-искомая

m

m

перпендикулярную к данной прямой
Дано:
прямая а
а
точка M
Построить:
m:
M∈m
m ⊥a
точка

М не принадлежит прямой а

М

Построение:

1. окр(М;г)

A

A1

2. окр(М;г)∩а={А;А1}

3. окр(А;АМ)

4. окр(А1;A1М)

5. окр(А;АМ)∩окр(А1;А1М)={M;Q}

Q

6. прямая МQ=m

7. m-искомая

m

m

перпендикулярную к данной прямой
Дано:
прямая а
а
точка M
Построить:
m:
M∈m
m ⊥a
точка

М не принадлежит прямой а

М

A

A1

Q

m

m

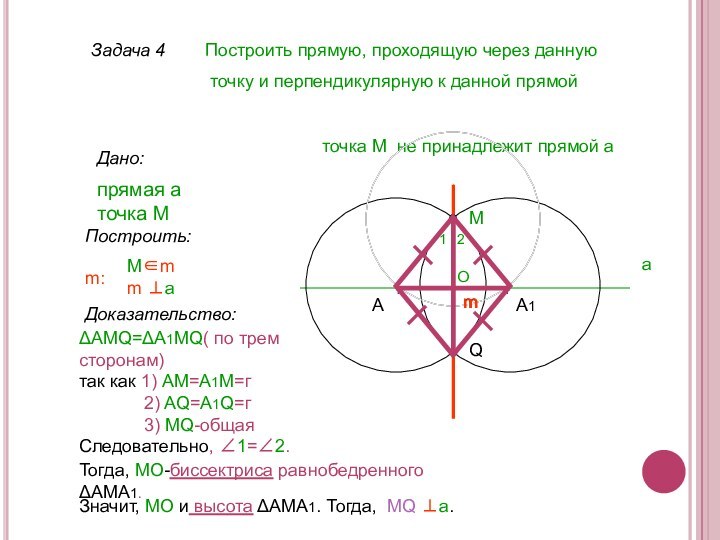
Доказательство:

ΔAМQ=ΔА1MQ( по трем сторонам)
так как 1) AM=А1M=г
2) AQ=A1Q=г
3) MQ-общая
Следовательно, ∠1=∠2.

Тогда, МО-биссектриса равнобедренного ΔАМА1.

1

2

О

Значит, МО и высота ΔАМА1. Тогда, МQ ⊥a.

ОМ
О
М
∠А
А
Построить:
Построение:
1. окр(А,г); г-любой

С
В
3. окр(О,г)

Е
4. окр(О,г) ∩ОМ= {Е}

5. окр(Е,ВC)

К

К1

6. окр(Е,BС)∩окр(О,г)= {К;К1}

7. луч ОК; луч ОК1

8. ∠КОМ -искомый

∠KOM=∠А

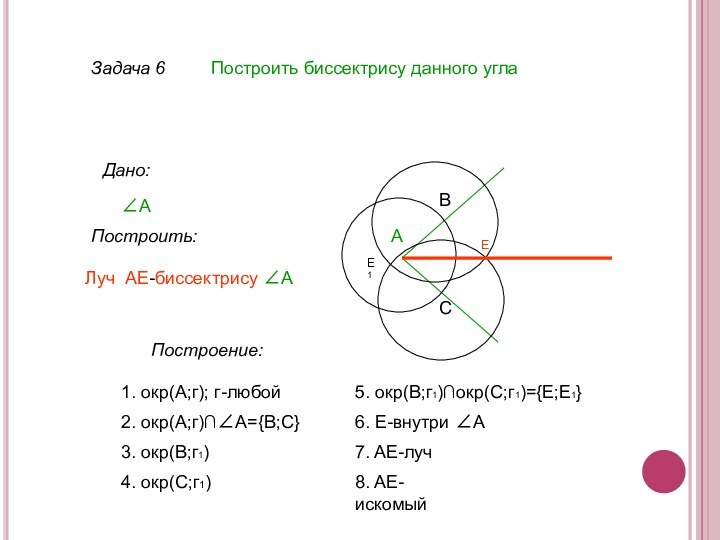
2. окр(А;г)∩∠А={В;С}

ОМ
О
М
∠А
А
Построить:

С
В

Е

К
К1
∠KOM=∠А
Доказательство:
ΔAВС=ΔОЕК(по трем сторонам)
так как 1) АВ=ОЕ=г
2)

АС=ОК=г
3) ВС=ЕК=г1

Следовательно, ∠КОМ=∠А

AE-биссектрису ∠А

2. окр(А;г)∩∠А={В;С}
C
B
3. окр(В;г1)
4. окр(С;г1)


E
E 1
5. окр(В;г1)∩окр(С;г1)={Е;E1}
6. Е-внутри ∠A

7. AE-луч

8. AE-искомый

Е