Слайд 2
ПЛАН
Введение
1. Из истории происхождения процентов
2. Решение задач на
проценты разными способами
3. Решение задач по формуле сложных процентов
4.
Решение задач на смеси и сплавы.
5. Применение процентов в жизни
Заключение
Список литературы
Слайд 3
Почему я выбрал тему «Проценты»?
Проценты - это одна
из сложнейших тем математики, и очень многие учащиеся затрудняются
или вообще не умеют решать задачи на проценты. А понимание процентов и умение производить процентные расчёты необходимы для каждого человека. Прикладное значение этой темы очень велико и затрагивает финансовую, экономическую, демографическую и другие сферы нашей жизни. Изучение процента продиктовано самой жизнью. Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни. Немецкий физик 18-го столетия Лихтенберг сказал: « То, что вы были принуждены открыть сами, оставляет в вашем уме дорожку, которой вы сможете снова воспользоваться, когда в том возникнет необходимость». Поэтому я решил и сделал подборку задач из ГИА - 9 классов, из ЕГЭ - 11 классов на банковские проценты, где применяется формула сложных процентов.
Слайд 4
Цель исследовательской работы
· Расширение знаний о применении
процентных вычислений в задачах и из разных сфер жизни
человека.
Слайд 5
Задачи:
· Познакомиться с историей возникновения процентов;
· Решать задачи
на проценты разными способами;
· Сделать подборку задач из ГИА
- 9 кл., ЕГЭ -11кл., решаемые по формуле сложных процентов;
· Поработать в текстовом редакторе;
· Поработать с ресурсами Internet;
· Получить опыт публичного выступления.
Слайд 6
История создания процентов.
В Европе в средние века
расширилась торговля и, следовательно, особое внимание обращалось на умение
вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином
Слайд 7
Решение задач на проценты разными способами
Задачи с
процентами можно решить разными способами:
уравнением;
составлением таблицы;
применяя
пропорцию;
по действиям;
используя правила.
Слайд 8
Решение задач на сложные проценты
Сложным процентом называется сумма
дохода, которая образуется в результате инвестирования денег при условии,
что сумма начисленного простого процента не выплачивается в конце каждого периода, а присоединяется к сумме основного вклада и в следующем платежном периоде сама приносит доход .
Сложные проценты - это проценты, полученные на начисленные проценты
Слайд 9
Формула сложного процента
х(1+ 0,01а)
где х -
начальный вклад, сумма.
а - процент(ы) годовых
n- время размещения вклада
в банке
х(1- 0,01а)
периодическое увеличение некоторой величины
на одно и то же число процентов
периодическое уменьшение некоторой величины
на одно и то же число процентов.
Слайд 10
Решение задач
Задача 1:
Вкладчик открыл счет в банке, внеся
2000 рублей на вклад, годовой доход по которому составляет
12%, и решил в течение шести лет не брать процентные начисления. Какая сумма будет лежать на счете через шесть лет?
Слайд 11
Решим эту задачу по формуле сложных
процентов.
первоначальный вклад
- 2000
процент годовых - 12
n - 6 лет, значит
2000(1 + 0,12) = 2000*1,126 = 2000*1,973823 = 3947,65
ОТВЕТ: через 6 лет на счете будет лежать сумма
в виде 3947 руб. и 65 коп..
Слайд 12
Задача 2:
После двух последовательных снижений цен на одно
и то же число процентов стоимость товара с 400
рублей снизилась до 324 рублей. На сколько процентов стоимость товара снижалась каждый раз?
Слайд 13
Решение:
400*(1-0,01а)=324
20(1 - 0,01а) = 18
1 - 0,01а =
0,9
а = 10
ОТВЕТ: стоимость товара каждый раз
снижалась на
10%
Слайд 14
Задача №3
В соответствии с договором фирма с целью
компенсации потерь от инфляции была обязана в начале каждого
квартала (3 месяца) повышать сотруднику зарплату на 2%. Однако в связи с финансовыми затруднениями она смогла повышать ему зарплату только раз в полгода (в начале следующего полугодия). На сколько % фирма должна повышать зарплату каждые полгода, чтобы первого января следующего года зарплата сотрудника была равна той, которую он получил бы в режиме повышения, предусмотренной договором?
Слайд 15
Решение:
Для решения составим таблицу
Слайд 16
По таблице составим уравнение:
х(1+0,02) = х(1+0,01а)²
(1+0,02)² = (1+0,01а)
1+0,04+0,0004=1+0,01а
0,0404=0,01а
а
= 4,04%
ОТВЕТ: через каждый полгода зарплату сотрудникам
надо поднимать
на 4,04%
Слайд 17
Решение задач на смеси и сплавы.
Задача 1.
При смешивании
5%-ного раствора кислоты с 40% -ным раствором кислоты получили
140г 30%-ного раствора. Сколько граммов каждого раствора было для этого взято?
Слайд 18
Рассмотрим старинный способ решения этой задачи.
Друг под другом
пишутся содержания кислот имеющихся растворов, слева от них и
примерно посередине – содержание кислоты в растворе, который должен получиться
после смешивания. Соединив написанные числа чёрточками получим такую схеме:
30
5
40
Рассмотрим пары 30 и 5, 30 и 40. В каждой паре из большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки . Получится такая схема:
10
30
5
40 25
Из неё делается заключение, что 5%-ного раствора следует взять 10 частей,
а 40% - ого 25 частей, т.е. для получения 140г. 30% - ого раствора нужно взять
5% - ого раствора 40г., а 40% - ого - 100г .(10+25=35частей всего, 140:35=4г-вес одной
части, 4×10=40г, 4×25=100г.)
Слайд 19
Задача 2.
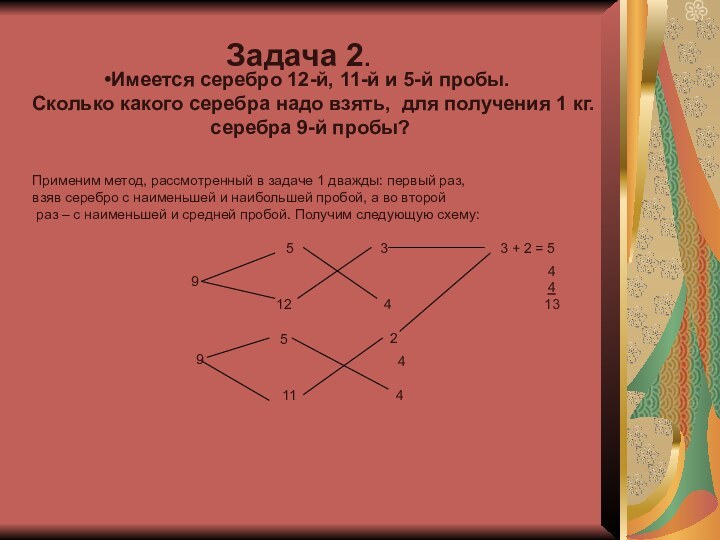
Имеется серебро 12-й, 11-й и 5-й пробы.
Сколько какого серебра надо взять, для получения 1 кг.
серебра 9-й пробы?
Применим метод, рассмотренный в задаче 1 дважды: первый раз,
взяв серебро с наименьшей и наибольшей пробой, а во второй
раз – с наименьшей и средней пробой. Получим следующую схему:
3 + 2 = 5
4
4
13
5
9
5
9
12
4
3
4
2
11
4
При этом найдены
доли , в которых нужно сплавлять серебро наибольшей и средней
пробы (4 и 4). Сложив затем доли серебра наименьшей пробы , найденные в первой и
во второй раз (3+2=5), получим долю серебра наименьшей пробы в общем сплаве.
Таким образом, надо взять
кг. серебра 5-й пробы,
кг. серебра 12-й пробы,
Данная задача имеет не единственное решение.
9-й пробы серебро можно получить , сплавляя серебро 5-й и 12-й пробы
в отношении 3:4(1сплав) или серебро 5-й и 11-й пробы в отношении 2:4(2 сплав).
Соединяя 1 и 2 сплавы в любой пропорции, мы будем получать
различные сплавы серебра 9-й пробы.
кг. серебра 11-й пробы.
Слайд 21
Задача 3.
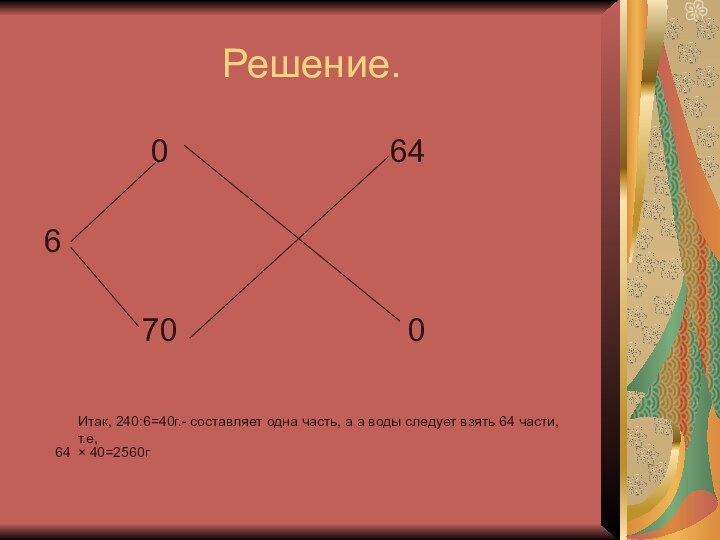
Имеется 240г. 70% -ого раствора уксусной кислоты.
Нужно получить 6% - ный раствор кислоты. Сколько граммов
воды (0%-ный раствор) нужно прибавить к имеющемуся раствору?
64
6
70 0
Итак, 240:6=40г.- составляет одна часть, а а воды следует взять 64 части, т.е,
× 40=2560г
64
Слайд 23
Применение процентов в жизни.
В настоящее время понимание процентов
и умение
производить процентные расчеты, необходимы
каждому человеку:
Прикладное значение этой
темы очень велико и
затрагивает финансовую, экономическую,
демографическую и другие сферы нашей жизни.
Изучение процента продиктовано самой жизнью.
Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни.
Слайд 24
Заключение.
Я выбрал эту тему потому, что мне нравится
математика и я считаю, что математику надо знать хорошо.
Я
хотел получить полноценные представления о процентах, об их роли в повседневной жизни.
Работа над данной темой , способствовала расширению
моего математического кругозора, развитию умения анализировать, сравнивать, глубоко и прочно усвоив материал.
Мне хочется порекомендовать ученикам формулу сложных
процентов и применять её при решении задач на проценты.