- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Золотое сечение в архитектуре 9 класс
Содержание
- 2. Золотое сечение (золотая пропорция, деление в крайнем и среднем
- 3. Число называется также золотым
- 4. История золотого сеченияПринято считать, что понятие о
- 5. Французский архитектор Ле Корбюзье нашел, что в
- 6. ПифагорКвадрат Пифагора и диагональ этого квадрата были
- 7. ЕвклидВ дошедшей до нас античной литературе золотое
- 8. Одним из красивейших произведений древнегреческой архитектуры является
- 9. Храм Василия Блаженного Трудно найти человека, который
- 10. Известный русский архитектор М. Казаков в своем
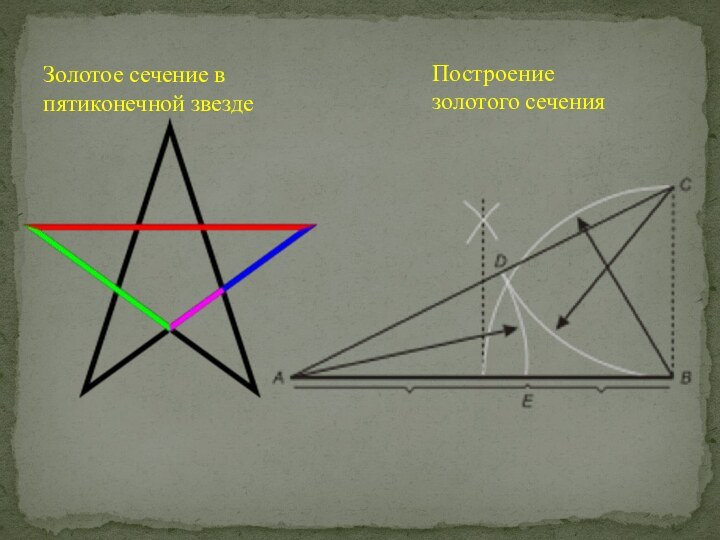
- 11. Золотое сечение в пятиконечной звездеПостроение золотого сечения
- 12. Ряд Фибоначчи
- 13. В 1202 г вышел в свет его
- 14. Подробный рассказ о порядке Фибоначчи
- 15. Отрезав квадрат от прямоугольника, построенного по принципу
- 16. Акварели Marlin Manson Картина «Фибоначчи»Леонардо Пизанский, также
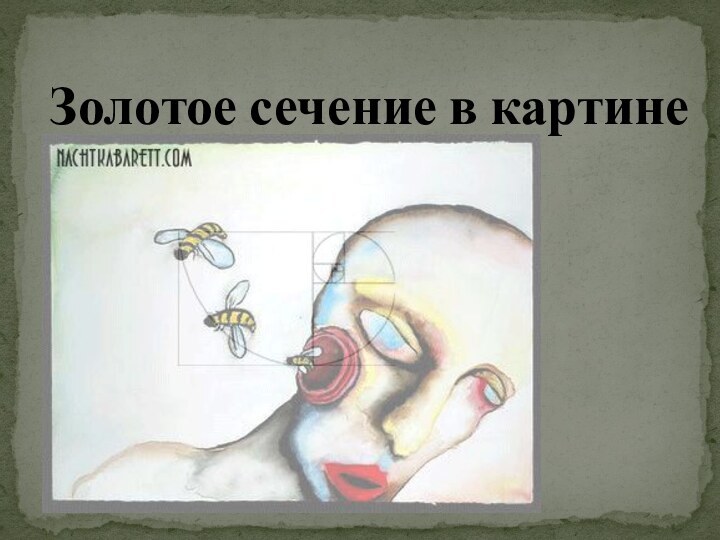
- 17. Золотое сечение в картине
- 18. Скачать презентацию
- 19. Похожие презентации
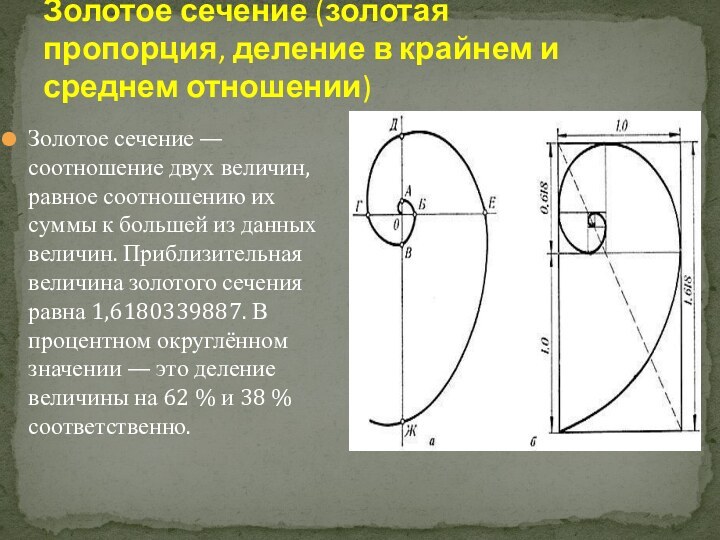
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении)Золотое сечение — соотношение двух величин, равное соотношению их суммы к большей из данных величин. Приблизительная величина золотого сечения равна 1,6180339887. В процентном округлённом значении — это деление величины














Слайд 3
Число называется также золотым числом.
С
математической точки зрения, отношение большей части к меньшей в
золотом сечении выражается квадратичной иррациональностьюи, наоборот, отношение меньшей части к большей
Слайд 4
История золотого сечения
Принято считать, что понятие о золотом
делении ввел в научный обиход Пифагор, древнегреческий философ и
математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их созданииСлайд 5 Французский архитектор Ле Корбюзье нашел, что в рельефе
из храма фараона Сети I в Абидосе и в
рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления
Слайд 6
Пифагор
Квадрат Пифагора и диагональ этого квадрата были основанием
для построения динамических прямоугольников . Платон (427...347 гг. до
н.э.) также знал о золотом делении.Платон
Слайд 7
Евклид
В дошедшей до нас античной литературе золотое деление
впервые упоминается в “Началах” Евклида. Во 2-й книге “Начал”
(ок. 300 лет до н. э.) дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), и др.Слайд 8 Одним из красивейших произведений древнегреческой архитектуры является Парфенон
(V в. до н. э.).
Парфенон имеет 8 колонн по
коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.
Слайд 9
Храм Василия Блаженного
Трудно найти человека, который бы
не знал и не видел собора Василия Блаженного на
Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследуя его, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения: 1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7, где j =0,618Слайд 10 Известный русский архитектор М. Казаков в своем творчестве
широко использовал “золотое сечение”.
Его талант был многогранным. Например, “золотое
сечение” можно обнаружить в архитектуре здания сената в Кремле.По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется больницей имени Н.И. Пирогова
Слайд 13 В 1202 г вышел в свет его математический
труд “Книга об абаке” (счетной доске), в котором были
собраны все известные на то время задачи. Одна из задач гласила “Сколько пар кроликов в один год от одной пары родится”. Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, и т.д.
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).
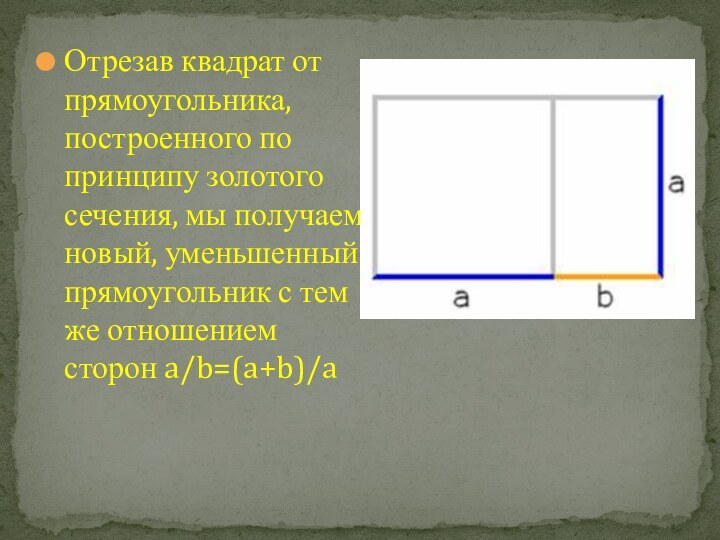
Слайд 15 Отрезав квадрат от прямоугольника, построенного по принципу золотого
сечения, мы получаем новый, уменьшенный прямоугольник с тем же
отношением сторон a/b=(a+b)/a
Слайд 16
Акварели Marlin Manson
Картина «Фибоначчи»
Леонардо Пизанский, также известный
как Фибоначчи — первый крупный математик средневековой Европы. Пчелы
символизируют трудолюбие и усердие, поэтому голова математика изображена в виде пчелиного улья. Кроме того для условного расположения элементов головы и пчел на полотне Мэнсон применил математический принцип Золотого сечения.В альбоме Marylin Manson “Holy Wood” количество ударов в начале каждой песни является числом последовательности Фибоначчи .
Marlin Manson – художник, писатель , певец , актер.