- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на построение по стереометрии
Содержание
- 2. В основании пирамиды лежит прямоугольный треугольник, один
- 3. Решение. В основании пирамиды
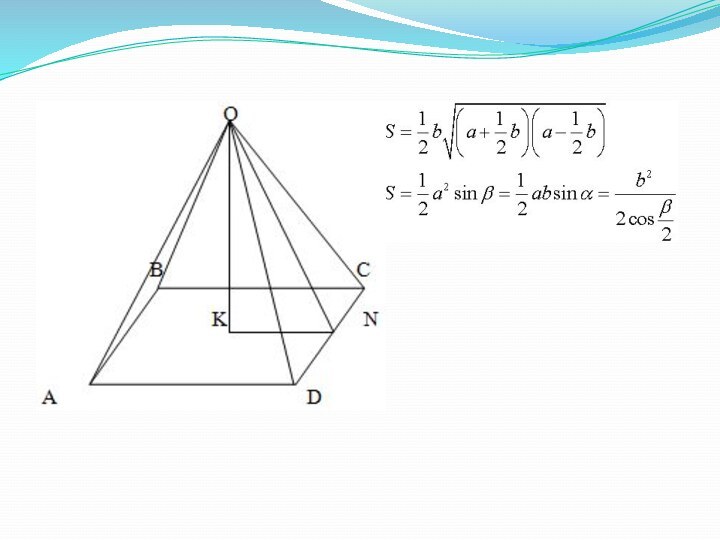
- 4. Задача. В правильной четырехугольной пирамиде сторона основания
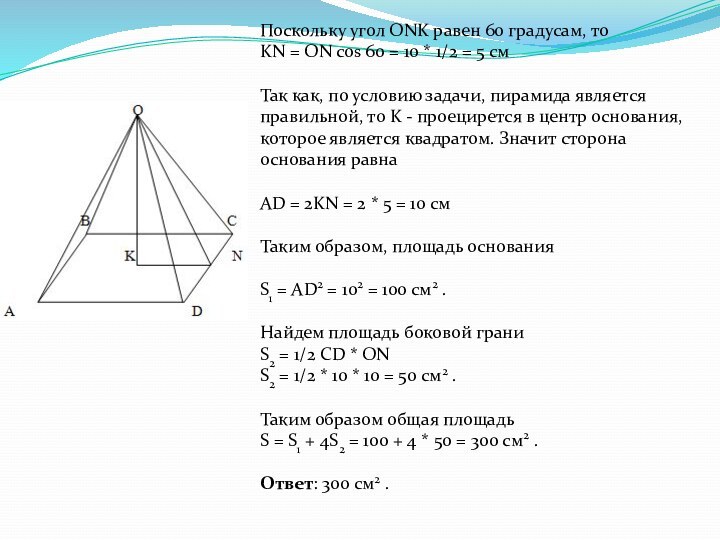
- 6. Исходя из свойств правильной пирамиды, каждая из
- 7. Задача. Высота правильной треугольной пирамиды 4 см,
- 9. Исходя из того,
- 10. Задача. Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3
- 11. Решение. Поскольку все ребра треугольной пирамиды равны
- 12. Задача. Высота боковой грани правильной четырехугольной пирамиды
- 13. Скачать презентацию
- 14. Похожие презентации
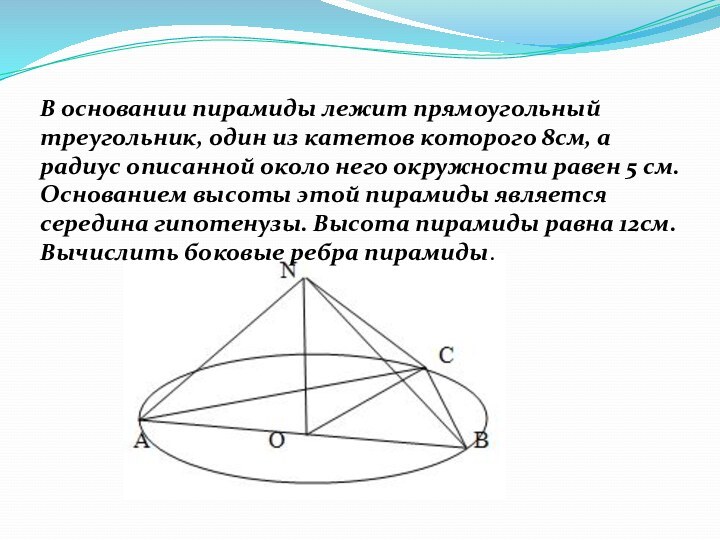
В основании пирамиды лежит прямоугольный треугольник, один из катетов которого 8см, а радиус описанной около него окружности равен 5 см. Основанием высоты этой пирамиды является середина гипотенузы. Высота пирамиды равна 12см. Вычислить боковые ребра пирамиды.