Презентация на тему по математике на тему Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке

в точке х=а , если выполняется соотношение

:

Функцию y=f(х) называют непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.

рациональных, иррациональных, тригонометрических выражений, то функция

непрерывна в любой точке, в которой определено выражение.

достигает на нем и своего наибольшего и своего наименьшего

значений.

как на концах отрезка, так и внутри него.
Наибольшее и

наименьшее значение достигается внутри отрезка.

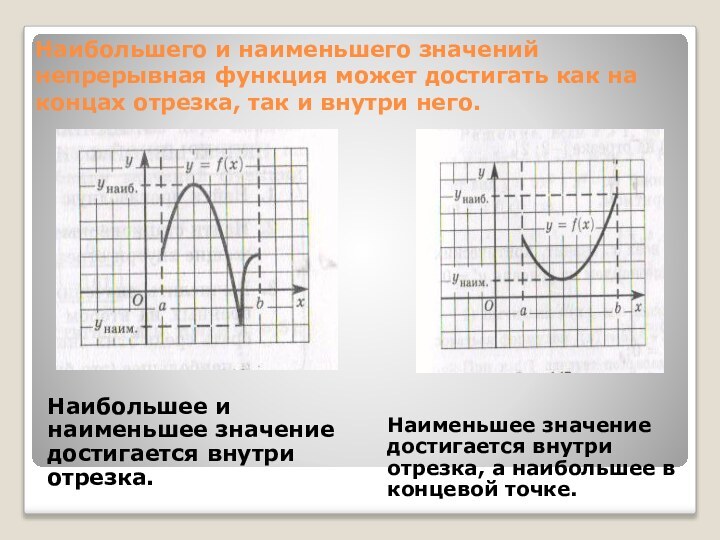
Наименьшее значение достигается внутри отрезка, а наибольшее в концевой точке.

только в стационарной или критической точке.

равна нулю, называют стационарными.

непрерывна, но производная не существует,- называют критическими.

y=f(х) на отрезке [а;в].
1.Найти производную

.
2.Найти стационарные и критические точки функции, лежащие внутри
отрезка [а;в] .
3.Вычислить значения функции y=f(х) в точках, отобранных на втором шаге, и в точках а и в , выбрать среди этих значений наименьшее (это будет ) и наибольшее (это будет ).

а) на отрезке ; б) на отрезке ; в) на отрезке ;

, значит, критических точек нет, а стационарные найдем

из условия

Имеем:




Дальнейшие рассуждения зависят
от условия задачи:

, и ) принадлежат

заданному отрезку

Значит, что на третьем шаге алгоритма мы составим
такую таблицу значений функции:








Таким образом,
(достигается в точке );
(достигается в точке ).

принадлежат лишь одна из двух найденных стационарных точек,

а именно точка .

Значит, на третьем шаге мы составим такую таблицу значений функции






Таким образом, (достигается в точке );
( достигается в точке ).