Презентация на тему по теме Математика-царица наук

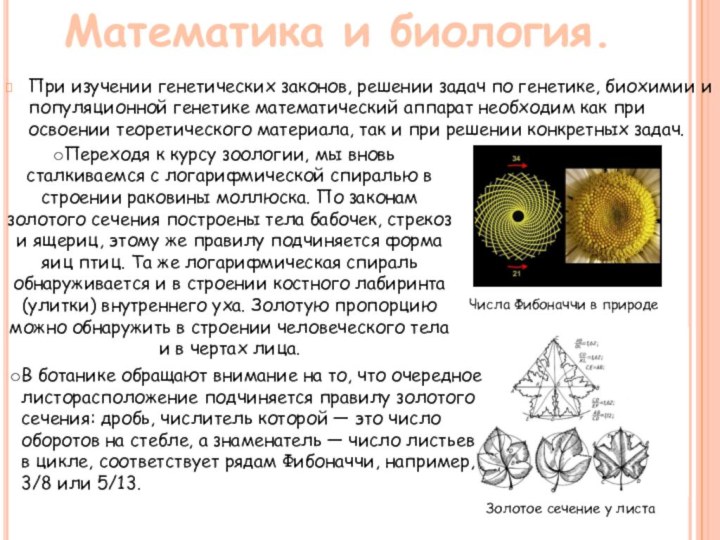
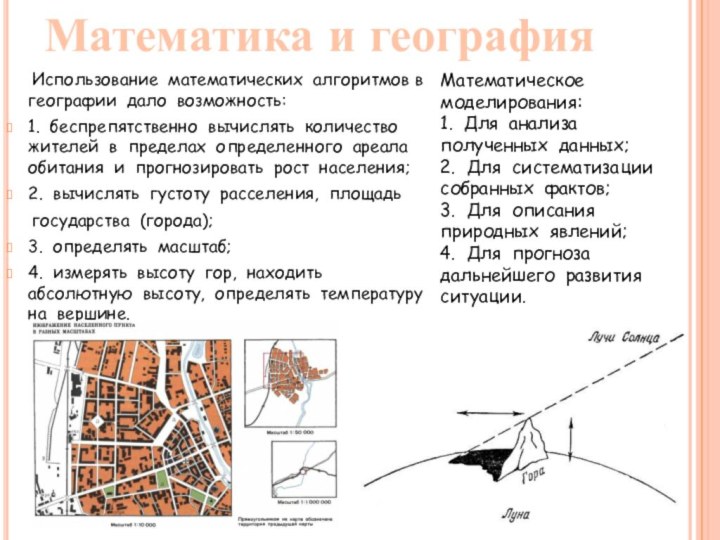
модели.

Например, графические упражнения, позволяющие перевести физическую ситуацию на

геометрический язык и получить информацию о механических явлениях решая системы задач с физическим содержанием при изучении темы «Векторы» в 8-9 классах на примере раздела «Динамика».
Закон Ньютона выражается математически как  F=ma. Это на самом деле пример модели, основанной на дифференциальном уравнении, поскольку ускорение есть вторая производная по времени. То есть в развернутом виде закон Ньютона выглядит как:
md2x(t)dt2=F(x)
С этой точки зрения физика —часть математики

по генетике, биохимии и популяционной генетике математический аппарат необходим

как при освоении теоретического материала, так и при решении конкретных задач.

Переходя к курсу зоологии, мы вновь сталкиваемся с логарифмической спиралью в строении раковины моллюска. По законам золотого сечения построены тела бабочек, стрекоз и ящериц, этому же правилу подчиняется форма яиц птиц. Та же логарифмическая спираль обнаруживается и в строении костного лабиринта (улитки) внутреннего уха. Золотую пропорцию можно обнаружить в строении человеческого тела и в чертах лица.

Золотое сечение у листа

Числа Фибоначчи в природе

В ботанике обращают внимание на то, что очередное листорасположение подчиняется правилу золотого сечения: дробь, числитель которой — это число оборотов на стебле, а знаменатель — число листьев в цикле, соответствует рядам Фибоначчи, например, 3/8 или 5/13.

химии, имеют дело с конкретными свойствами атомов и молекул.

В современной химии для определения структуры молекул (их геометрического строения) используют разнообразные физические методы, наиболее распространённые из которых – инфракрасная спектроскопия (ИК), спектроскопия ядерного магнитного резонанса (ЯМР) и масс-спектроскопия (MS).

Метод пропорции в математики и химии.
Пропорция - равенство двух отношений:a/b=c/d , где b и d
не равны нулю.
(a, d - крайние члены пропорции; b, c - средние члены пропорции). Основное свойство пропорции: ad=bc.
С помощью линейных уравнений в химии мы можем легко вычислить степень окисления химического элемента в сложном веществе.

географии дало  возможность:
1.  беспрепятственно  вычислять  количество  жителей  в 

пределах  определенного  ареала  обитания  и  прогнозировать  рост  населения;
2.  вычислять  густоту  расселения,  площадь 
государства  (города);
3.  определять  масштаб;
4.  измерять  высоту  гор,  находить  абсолютную  высоту,  определять  температуру  на  вершине.

Математическое моделирования:
1.  Для  анализа  полученных  данных;
2.  Для  систематизации  собранных  фактов;
3.  Для  описания  природных  явлений;
4.  Для  прогноза  дальнейшего  развития  ситуации.

Первое - это теорема Пифагора, второе - деление отрезка

в крайнем и среднем отношении, которое носит название «золотое сечение». Золотое сечение математики можно рассмотреть на примере композиции “Пиковой дамы” Пушкина. В повести 853 строчки. Кульминацией является сцена в спальне графини, куда проник Герман в надежде узнать тайну 3-х карт. Смерть графини от испуга случается на 535 строке. Эта строка располагается точно в месте золотого сечения, так как 835:535=1,6. В повести “Пиковая дама” 6 глав. И в каждой главе проявляется правило золотого сечения. Золотое сечение в композиции повести “Пиковая дама” – убедительное подтверждение того, что творчество Пушкина основывалось на интуиции, которая подчиняется точным математическим расчётам.

Многие произведения Пушкина, например стихи, тесно связаны не только с правилом «золотого сечения», но и с числами Фибоначчи. Наиболее часто в творчестве поэта встречаются стихи с таким количеством строк, которые тяготеют к данной числовой последовательности: 5, 8, 13, 21, 34. Наиболее выдающиеся шедевры, состоящие из 8 строчек, – это “Я вас любил”, “Пора, мой друг, пора! Покоя сердце просит”

назад для строительства пирамид использовали метод получения прямоугольного треугольника

при помощи верёвки разделенной на 12 равных частей.
Уже в каменном веке арифметика была важной частью жизни людей.Первыми понятиями математики были "меньше", "больше" и "столько же". Если одно племя меняло пойманных рыб на сделанные людьми другого племени каменные ножи, не нужно было считать, сколько принесли рыб и сколько ножей. Достаточно было положить рядом с каждой рыбой по ножу, чтобы обмен между племенами состоялся.
Чтобы с успехом заниматься сельским хозяйством, понадобились арифметические знания. Без подсчета дней трудно было определить, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.

видом искусства, поскольку в ней обнаруживается своеобразная красота
Невозможные фигуры

- эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Наиболее известные невозможные фигуры: невозможный треугольник, бесконечная лестница и невозможный трезубец.
Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один из концов полоски, а затем склеив оба конца друг с другом.
Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство
Древнейшим литературным памятником, в котором встречается «Золотое сечение», являются «Начала» Евклида (3 в. до н.э.). Известно, что о золотом сечении знали Пифагор и его ученики (6 в. до н.э.)

Лента Мебиуса

Невозможная фигура

«Чёрный квадрат»
Малевича

время движения на спуске туловище лыжника должно быть параллельно

к склону, чтобы избежать сопротивления воздуху, или несколько выпрямлено. Лыжник должен знать законы, позволяющие ему двигаться с большой скоростью.
При подготовке команд и их тренеров к серьезной схватке с соперниками все математические методы работают как никогда. Например, определение оптимального состава на игру в футбольном матче, оптимальной расстановки игроков на футбольной поле, учет командного взаимодействия.
Обратимся к самому «математическому» виду спорта – шахматам ! Здесь используют теорию вероятности .В самом начале партии игрок имеет 20 вариантов для первого хода; его партнер может ответить 20 ходами на каждый ход, то есть в распоряжении последнего уже 400 вариантов только для первого хода!