- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интеллектуальный марафон
Содержание
- 3. Сколько животных и их образов скрыл в своей картине Стивен Гарднер?
- 4. Сколько птиц и их образов скрыто в картине Стивена Гарднера?
- 5. На рисунке изображены два одинаковых по форме
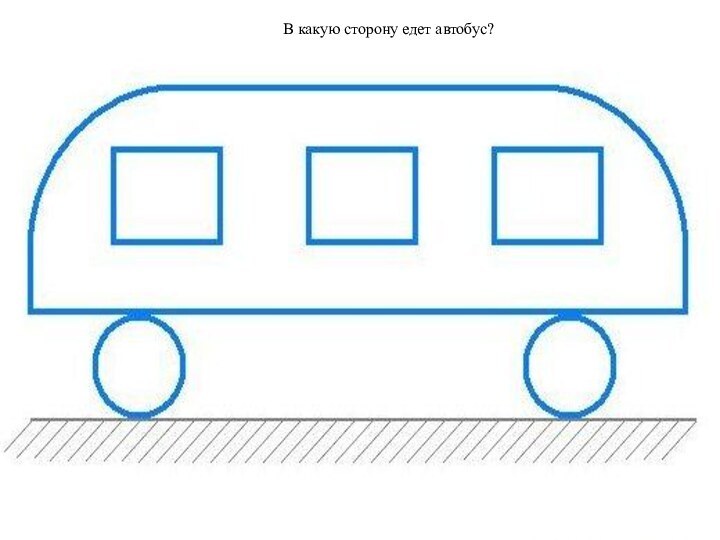
- 6. В какую сторону едет автобус?
- 8. 1.Рассмотрим метод Шерлока Холмса. Пусть нам предложена
- 10. Если в 12 часов ночи идет
- 12. 1. Необходимо выстроить цепочку из 10 вопросов,
- 14. На рисунке изображены семеро поросят. При помощи
- 16. Каким образом необходимо пересадить эти деревья, чтобы
- 18. Объемная фигура собрана из одинаковых кубиков, соединенных
- 20. Соедините попарно фигуры, имеющие одинаковую нумерацию, произвольными
- 23. Какой из этих двух мальчиков сможет принести в своей лейке больше воды для полива огорода? Почему?
- 24. Несмотря на то, что у
- 25. Как Вы считаете, какие буквы русского алфавита
- 26. За той карточкой, что
- 28. Предложите свое решение проблемы.1. Однажды ребята заблудились
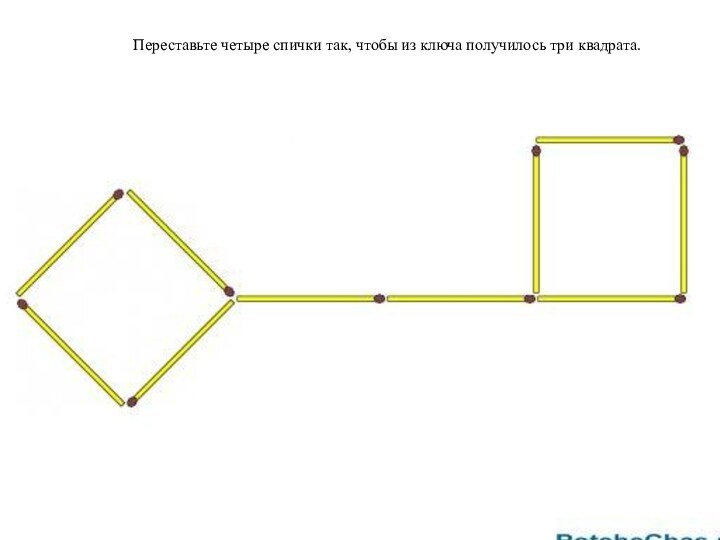
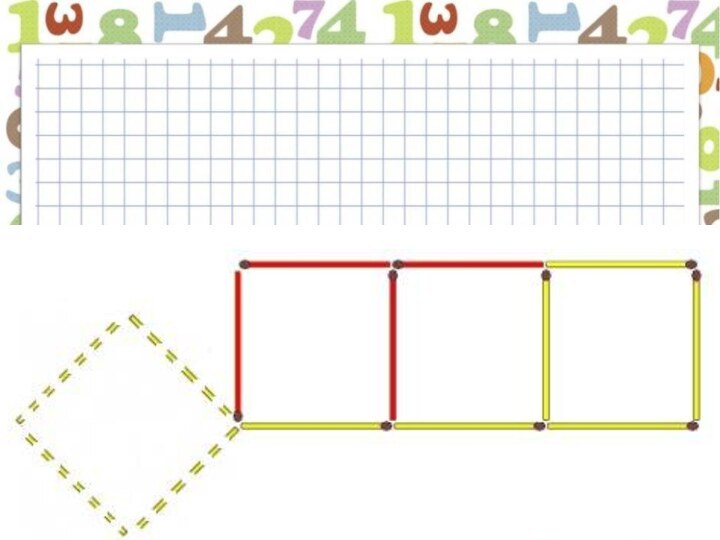
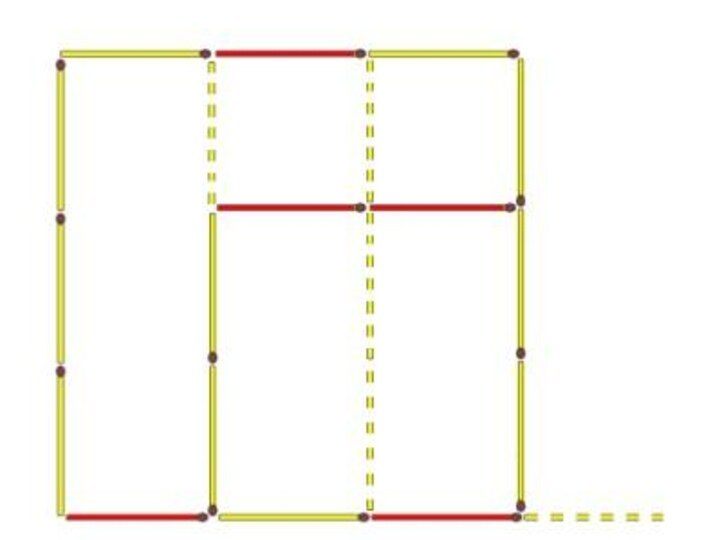
- 30. Переставьте четыре спички так, чтобы из ключа получилось три квадрата.
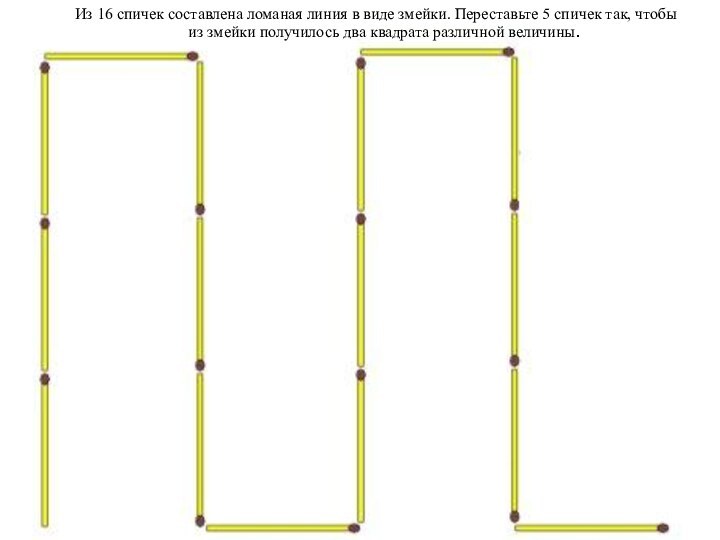
- 32. Из 16 спичек составлена ломаная линия в
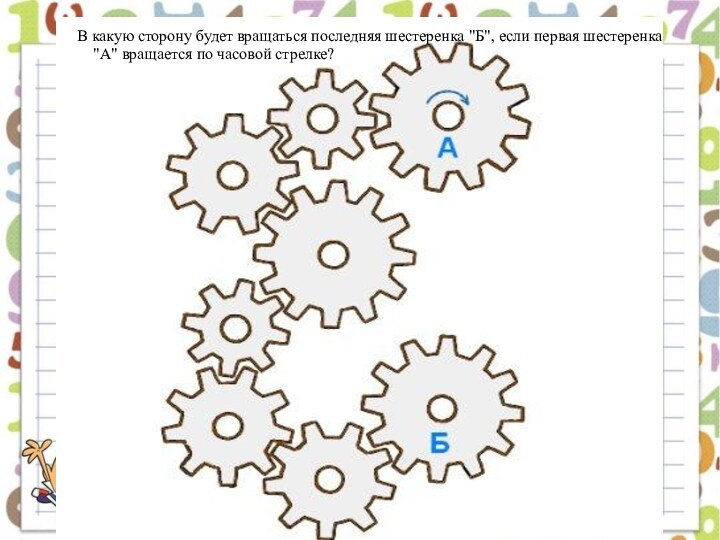
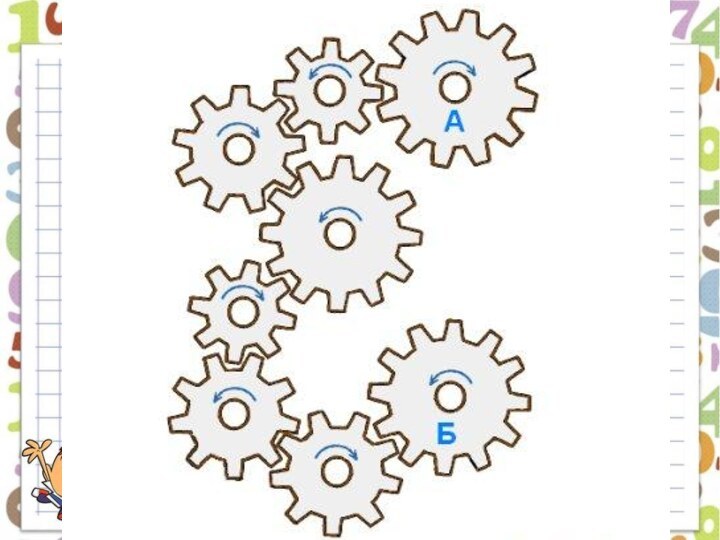
- 35. В какую сторону будет вращаться последняя шестеренка
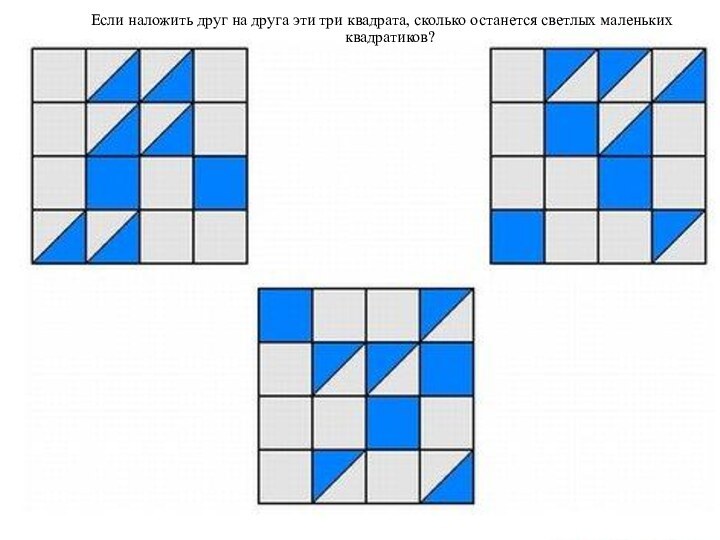
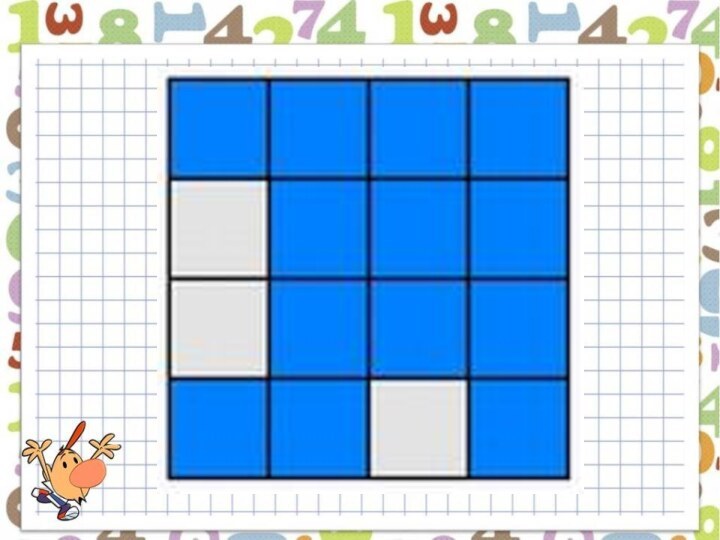
- 37. Если наложить друг на друга эти три квадрата, сколько останется светлых маленьких квадратиков?
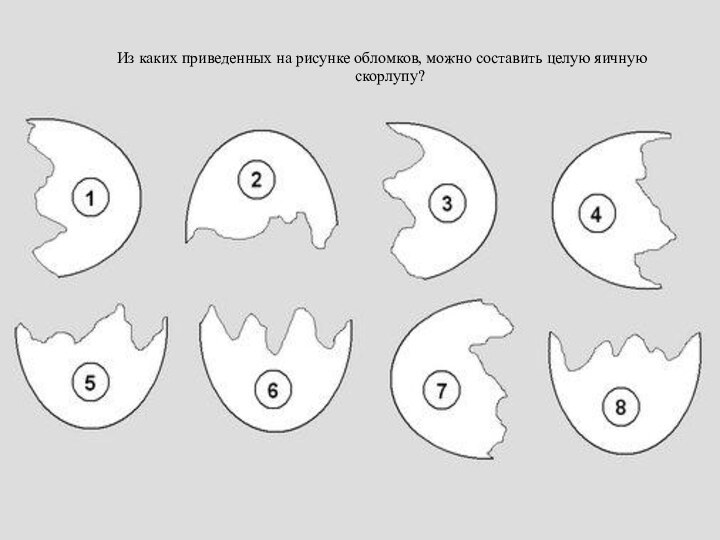
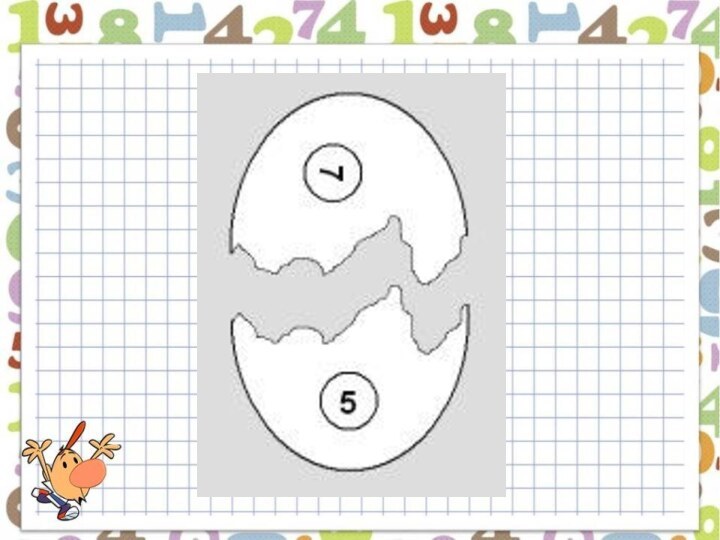
- 39. Из каких приведенных на рисунке обломков, можно составить целую яичную скорлупу?
- 41. Сосчитай треугольники ответ: 17
- 42. Скачать презентацию
- 43. Похожие презентации
Сколько животных и их образов скрыл в своей картине Стивен Гарднер?























Слайд 5
На рисунке изображены два одинаковых по форме сектора.
Одинаковы ли по величине эти два сектора? Если Вы
считаете, что они неодинаковы, то тогда определите, какой из них больший, а какой меньший. Аргументируйте свой ответ.Слайд 8 1.Рассмотрим метод Шерлока Холмса. Пусть нам предложена подсистема,
и требуется назвать как можно больше систем, для которых
она является частью. Например, подсистема – ручка. Она может быть частью тела ребенка, двери и так далее.Подсистема – корень.
2.Назовите целую систему по ее частям. Например: точки, отрезки, углы – это части системы геометрическая фигура.
Части подсистемы:
арифметика, алгебра, геометрия
луч, точка, абсцисса, ордината
снег, подошва
цифры, слова, знаки препинания.
3.Найдите систему, если даны подсистема и надсистема. Например: Подсистема – колесо, система - _______, надсистема – транспорт. Системой может быть – автомобиль, троллейбус, велосипед, самокат и так далее.
Подсистема – парта, система - ____________, надсистема – школа.
Подсистема – парус, система - ____________, надсистема – корабль.
Подсистема – число, система - ____________, надсистема – множество.
Слайд 10 Если в 12 часов ночи идет дождь, то
можно ли ожидать, что через 72 часа будет солнечная
погода?(Нет, так как через 72 часа снова будет полночь.)
Как защищают свои издания от пиратов, которые хотели бы их скопировать, некоторые издатели словарей и атласов?
(Обычно издатели включают в словарь несуществующее слово, а в атлас помещают несуществующий остров. Если они обнаруживаются в каком-то другом издании, факт копирования становится несомненным.)
3. Имеется 10 мешков с монетами (количество монет в каждом мешке одинаковое). В девяти мешках монеты золотые, а в одном - фальшивые. Вес настоящей золотой монеты 5 грамм, а вес фальшивой - 4 грамма. Как за одно взвешивание на весах (весы взвешивают с точностью до грамма) определить, в каком из мешков монеты фальшивые?
(Пронумеруем мешки от 1 до 10. Из первого мешка возьмем 1 монету, со второго 2, из третьего 3, и так до 10 (суммарно 55 монет). Произведем взвешивание этих монет. Если бы все монеты были золотыми, то весили бы 275 грамм. Если при нашем взвешивании не будет хватать 1 грамма, то фальшивые монеты в первом мешке, если 2-х грамм - то во втором, и так далее до 10-ти.)
4. Почему блюдце всегда имеет кольцевидную каемку с нижней стороны?
(Блюдце, тарелка или чашка - должны ровно стоять на горизонтальном столе. Для этого их дно шлифуется, но шлифовать всю поверхность дна было бы дорого и долго. Гораздо легче отшлифовать только кольцевую кромку дна.)
Слайд 12 1. Необходимо выстроить цепочку из 10 вопросов, начинающихся
словом «Зачем».
1. Зачем построена школа?
Чтобы получать знания.
2. Зачем получать
знания?Чтобы быть образованным.
3. Зачем быть образованным? …
2. Требуется назвать 7 предметов, которые выполняют функцию и антифункцию. Пример: ключ замок запирает и отпирает.
3. Необходимо перечислить 8 предметов, которые можно сделать из стекла.
4. Нужно описать книгу по плану:
Для чего она написана?
Из каких частей стоит?
Из чего сделаны части?
Почему они так сделаны?
Какие у них функции?
Как именно они сделаны?
Какие есть недостатки?
Как избавиться от недостатков?
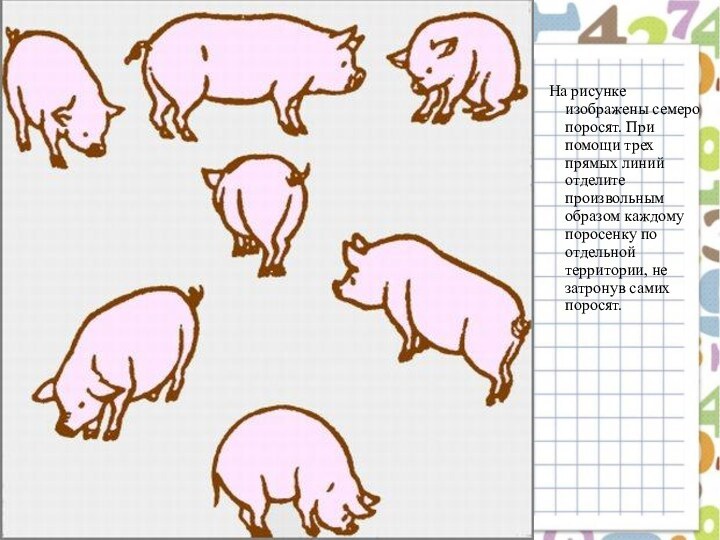
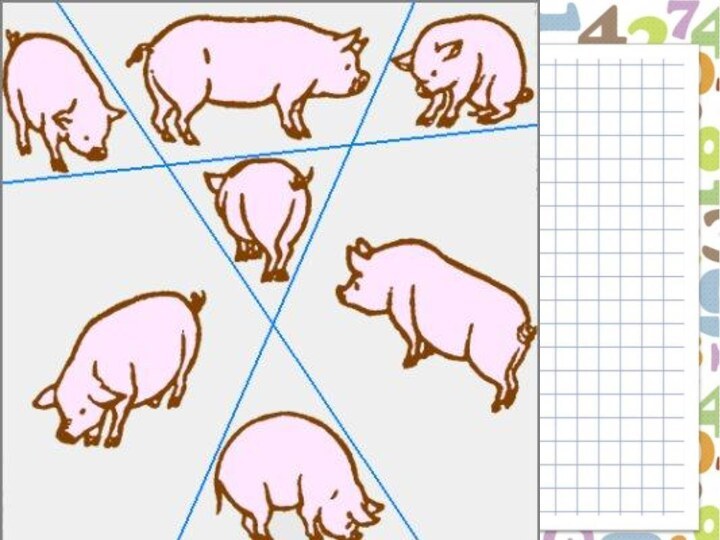
Слайд 14 На рисунке изображены семеро поросят. При помощи трех
прямых линий отделите произвольным образом каждому поросенку по отдельной
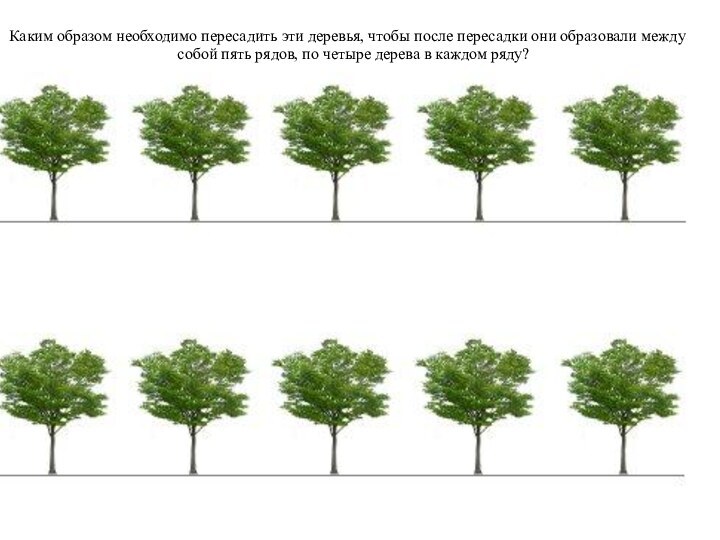
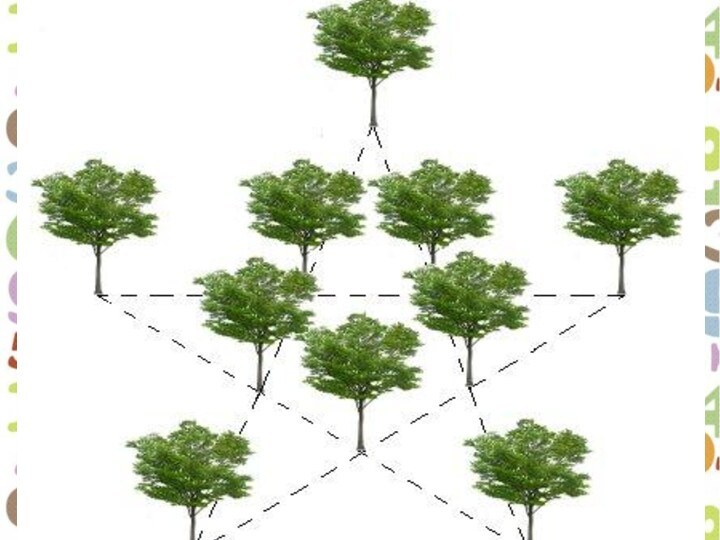
территории, не затронув самих поросят.Слайд 16 Каким образом необходимо пересадить эти деревья, чтобы после
пересадки они образовали между собой пять рядов, по четыре
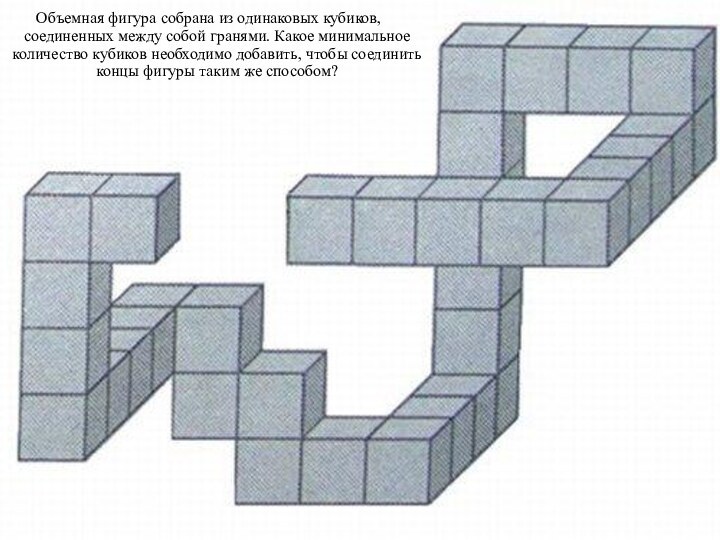
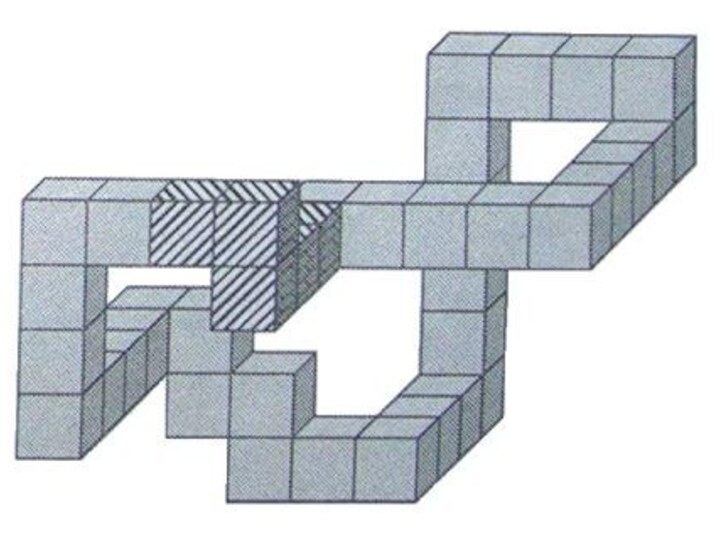
дерева в каждом ряду?Слайд 18 Объемная фигура собрана из одинаковых кубиков, соединенных между
собой гранями. Какое минимальное количество кубиков необходимо добавить, чтобы
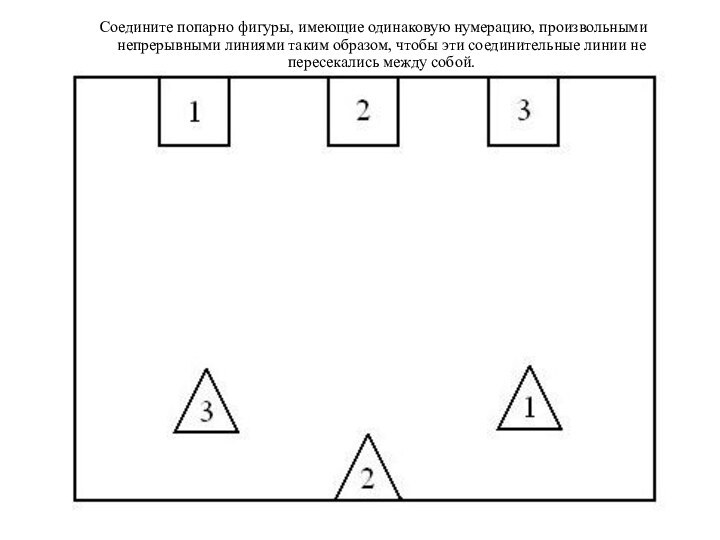
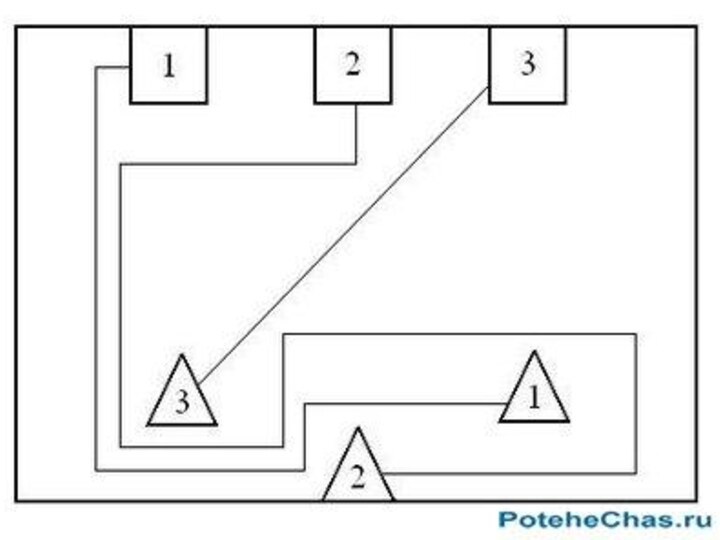
соединить концы фигуры таким же способом?Слайд 20 Соедините попарно фигуры, имеющие одинаковую нумерацию, произвольными непрерывными
линиями таким образом, чтобы эти соединительные линии не пересекались
между собой.Слайд 23 Какой из этих двух мальчиков сможет принести в
своей лейке больше воды для полива огорода? Почему?
Слайд 24
Несмотря на то, что у одного
мальчика лейка больше по размерам, оба мальчика принесут одинаковое
количество воды, так как носики у обеих леек находятся на одном уровне, и по закону физики о сообщающихся сосудах — уровень воды в лейках не превысит уровня, на котором располагаются края носиков леек. То есть лишняя вода просто вытечет.Слайд 25 Как Вы считаете, какие буквы русского алфавита могут
быть скрыты за карточками? Допускается расположение букв в любой
ориентации на плоскости.
Слайд 26
За той карточкой, что слева
— буквы "Ж", "К", "Х". За той карточкой, что
справа — буквы "Б", "В", "Е", "Р", "Ш", "Ь", "Э".
Слайд 28
Предложите свое решение проблемы.
1. Однажды ребята заблудились в
лесу, и попали в руки к злому волшебнику. «Я
все могу, - сказал он, и отпущу вас, если вы придумаете, что я не могу». Как вы думаете, что ответили ребята?2. Придумайте модель абсолютно безопасного бассейна для детей.
3. Черная фея делает злые дела с помощью волшебной палочки. Если отнять у нее палочку, то она умрет, но умрет и тот, кто возьмет ее в руки. Как быть?





























