Презентация на тему Подготовка к ЕГЭ (решение планиметричекских задач)

Содержание

2. Как взаимно располагаются две окружности?
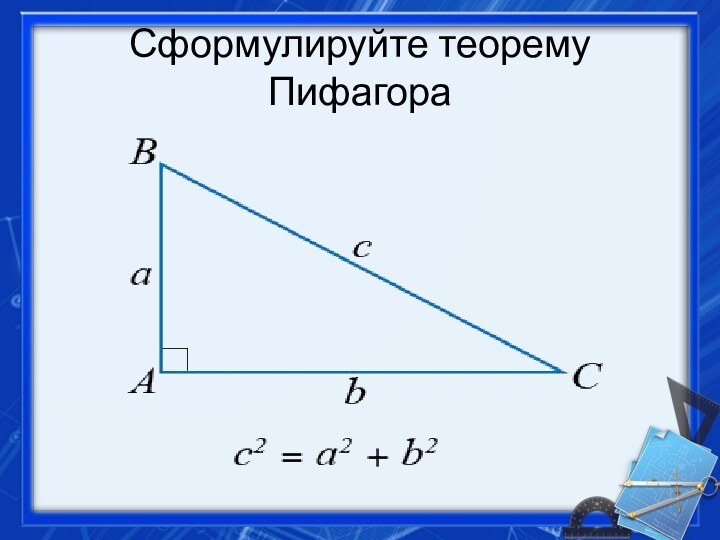
3. Сформулируйте теорему Пифагора
4. Сформулируйте теорему об угле между касательной
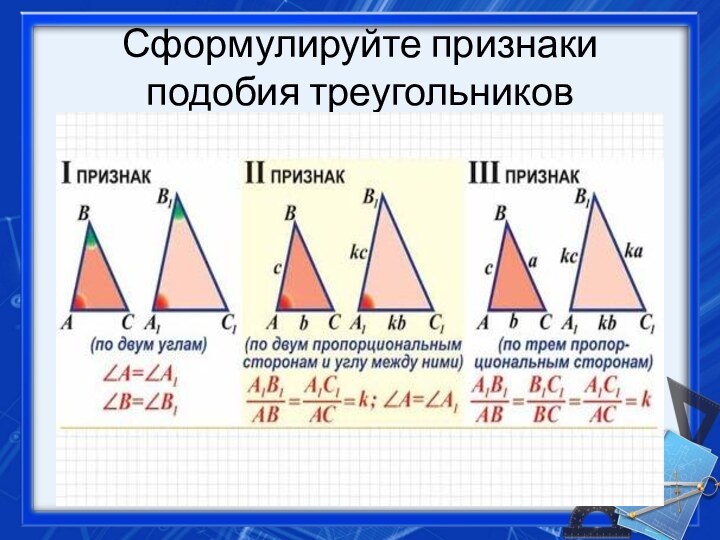
5. Сформулируйте признаки подобия треугольников
6. Задача: Две окружности касаются внутренним
7. Дано: О1, О2О1 ⋂ О2-СВ ∈ О2,А
8. Решение а) CL — общая касательная
9. Решение б)Рассмотрим треугольники ACD и ЕСВ ∠
10. Скачать презентацию
11. Похожие презентации

Как взаимно располагаются две окружности?

Главная
Образование
Подготовка к ЕГЭ (решение планиметричекских задач)

Подготовка к ЕГЭ (решение планиметрических задач)Выполнила: Чурина Елена Вениаминовна, учитель первой квалификационной

Как взаимно располагаются две окружности?

Сформулируйте теорему об угле между касательной и хордой Величина угла,

Сформулируйте признаки подобия треугольников

Задача: Две окружности касаются внутренним образом в точке С. Вершины

Дано: О1, О2О1 ⋂ О2-СВ ∈ О2,А ∈ О1АС О2-ЕВС

Решение а) CL — общая касательная двух окружностей, причём точки L

Решение б)Рассмотрим треугольники ACD и ЕСВ ∠ АСВ -общий,∠ CAD= ∠ CEB

http://www.anypics.ru/pic/201301/1280x1024/anypics.ru-57647.jpg -синий фон с чертежом http://lenagold.narod.ru/fon/clipart/l/line/rulla009.png - линейка, транспортирАвтор шаблона: Гусева Наталья

Слайды презентации

Слайд 2 Как взаимно располагаются две окружности?

Слайд 3 Сформулируйте теорему Пифагора

Слайд 4 Сформулируйте теорему об угле между касательной и хордой

Сформулируйте теорему об угле между касательной и хордой Величина угла, образованного касательной и хордой,

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна

половине величины дуги, заключённой между его сторонами.

Слайд 5 Сформулируйте признаки подобия треугольников

Слайд 6 Задача: Две окружности касаются внутренним образом

в точке С. Вершины A и B равнобедренного прямоугольного

треугольника ABC с прямым углом C лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите АС, если радиусы окружностей равны 3 и 4.

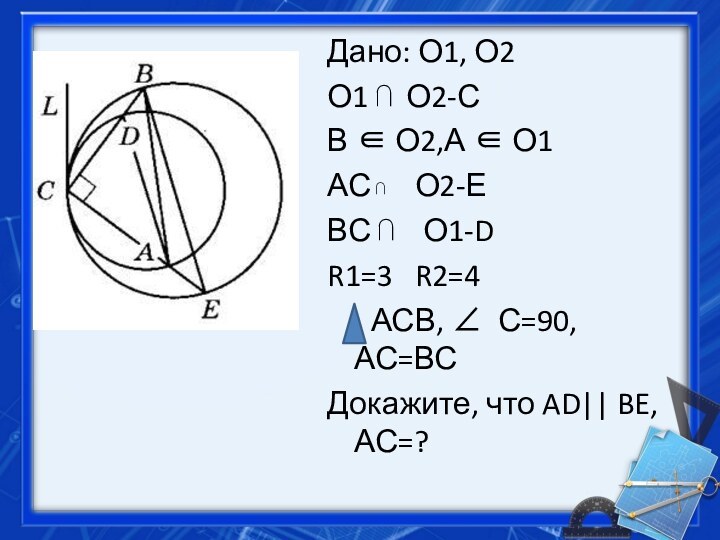
Слайд 7 Дано: О1, О2
О1 ⋂ О2-С
В ∈ О2,А ∈

О1
АС О2-Е
ВС ⋂ О1-D
R1=3 R2=4

АСВ, ∠ С=90, АС=ВС
Докажите, что AD|| BE, АС=?

⋂

Слайд 8 Решение а)
CL — общая касательная двух

окружностей, причём точки L и В лежат по одну

сторону от прямой АС. =>
∠ CAD= ∠ LCB
∠ LCB= ∠ CEB (по теореме об угле между касательной и хордой) => ∠ CAD= ∠ CEB
∠ CAD и ∠ СЕВ соответственные углы, образованные прямыми AD и BE и секущей СЕ => прямые AD и BE параллельны (по признаку параллельности прямых

Слайд 9 Решение б)
Рассмотрим треугольники ACD и ЕСВ
∠ АСВ

Решение б)Рассмотрим треугольники ACD и ЕСВ ∠ АСВ -общий,∠ CAD= ∠

-общий,
∠ CAD= ∠ CEB =>
▲ ACD ~

▲ ЕСВ (по двум углам)
Пусть АС = ВС = x, AD и ЕВ-диаметры окружностей => AD : ЕВ =3:4 =>CD:BC=3:4 =>
CD=3х/4 АD=R1+R1=6
▲ ACD-прямоугольный. По теореме Пифагора составим и решим уравние:
Х=4,8 Ответ: АС=4,8