формуле Ньютона – Лейбница, используя знания о первообразной и
правила её вычисления;Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции;
Закрепить изученное в ходе выполнения упражнений.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


![Презентация Интеграл. Формула Ньютона-Лейбница Определение:Пусть дана положительная функция f(x), определенная на конечном отрезке [a;b].Интегралом от функции](/img/tmb/13/1210949/3cfac8bc48a64c92be11fa249f860da4-720x.jpg)






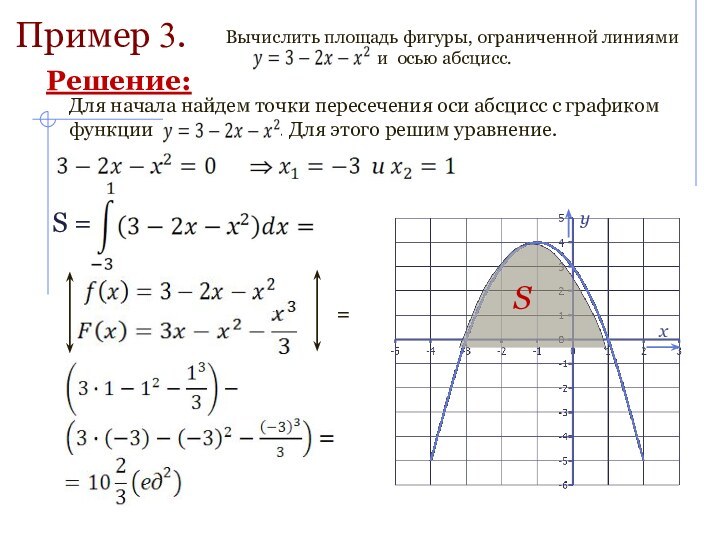
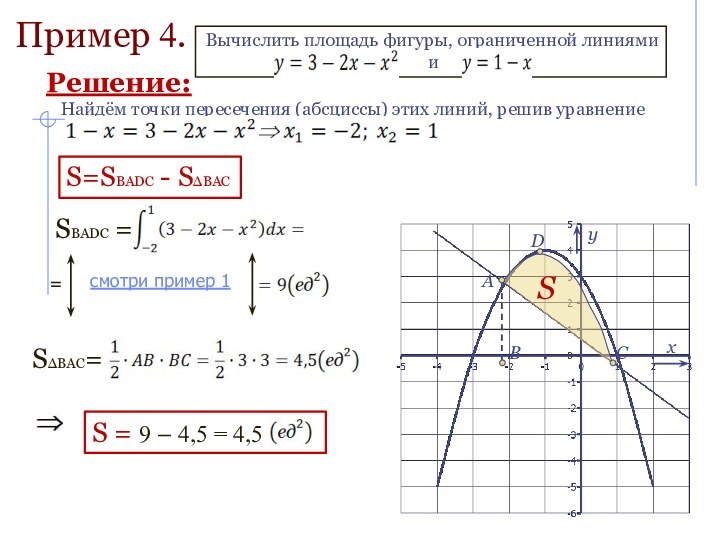





Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции;
Закрепить изученное в ходе выполнения упражнений.
Summa
Исаак Ньютон
Готфрид Вильгельм
фон Лейбниц
Якоб Бернулли