Презентация на тему Красота геометрических форм

2: На протяжении веков человек испытывает почти мистическую привязанность

к правильным, симметричным и гармоничным фигурам. Философы, геометры, художники считали чисто геометрические формы эталонами совершенства и красоты. Великие пирамиды Гизы – пример такого совершенства. http://lifeglobe.net/photos/neobychnue-piramidy/egipetskie Слайд 3: Геометрические тела, выполненные из разных материалов: бумага, металл, дерево. http://bit-player.org/2006/math-baubles https://polyhedronists.deviantart.com/art/dodecahedron-2-446453413 http://bulatov.org/metal/metal_all.html Слайд 4: Скульптор Келвин Зайберт (Calvin Seibert) создает сложные конструкции замков из песка, в виде геометрических фигур. Для создания фигур правильной геометрической формы, Келвину требуется пластиковый шпатель, и немножко фантазии... http://newsdj.ru/post267233225 Слайд 5: Многогранники издавна использовались для изготовления игральных костей: так, археологами была найдена этрусская игральная кость в форме додекаэдра, датируемая 1000 годом до н.э. Во множестве стран Западной и Центральной Европы при раскопках поселений эпохи Римской империи время от времени находят сравнительно небольшие, от 4 до10 сантиметров в поперечнике, бронзовые додекаэдры с круглыми отверстиями разных размеров, вершины которых украшены сферами. До сих пор не ясно, как использовались эти прекрасные фигуры. http://masterok.livejournal.com/2346904.html https://ru.wikipedia.org/wiki/%D0%A0%D0%B8%D0%BC%D1%81%D0%BA%D0%B8%D0%B9_%D0%B4%D0%BE%D0%B4%D0%B5%D0%BA%D0%B0%D1%8D%D0%B4%D1%80 Слайд 6: Мы не вполне осознаем, что многогранники постоянно присутствуют вокруг нас, поскольку они имеют разные формы,цвета и текстуры. И все же они прочно вошли в нашу жизнь, не только украшая ее но и выполняя различные полезные функции. В настоящее время необычайно популярны флорариумы из стекла. Они могут принимать самые разные многогранные формы. http://www.imgrum.org/tag/%D1%86%D0%B2%D0%B5%D1%82%D1%8B%D0%B8%D1%81%D1%82%D0%B5%D0%BA%D0%BB%D0%BE Слайд 7: Красочные денежные скульптуры канадской визуальной художницы Кристи Мэлэкофф «Денежные Кусочки». http://factologia.net/art/143-bills.html Слайд 8: Звездчатая форма додекаэдра от NORAH GAUGHAN. http://mizrah.ru/post172827822 Слайд 9, 11: Модели в технике кусудама. http://tigreshenka.livejournal.com/photo/album/301/?page=1 Слайд 10: Особым богатством форм отличаются такие предметы интерьера, как светильники. Во многих городах мира изготавливают прекрасные светильники, имеющие форму звездчатого многогранника. Например, такой.

при изучении ботаники, зоологии и геологии, всегда вызывают большой

интерес, в том числе из-за своей сложной формы, но не меньший интерес вызывают и простые формы, обладающие определенной симметрией. Эрнст Геккель, сопровождавший Чарльза Дарвина в его путешествиях, описал радиолярии – одноклеточные существа, по форме напоминающие правильные и звездчатые многогранники. Белковые структуры большинства вирусов имеют форму многогранников, например, структура ВИЧ представляет собой правильный икосаэдр. В геологии часто встречаются молекулы, имеющие форму многогранников, однако, наиболее удивительные многогранники образуются при росте кристаллов на макроуровне. 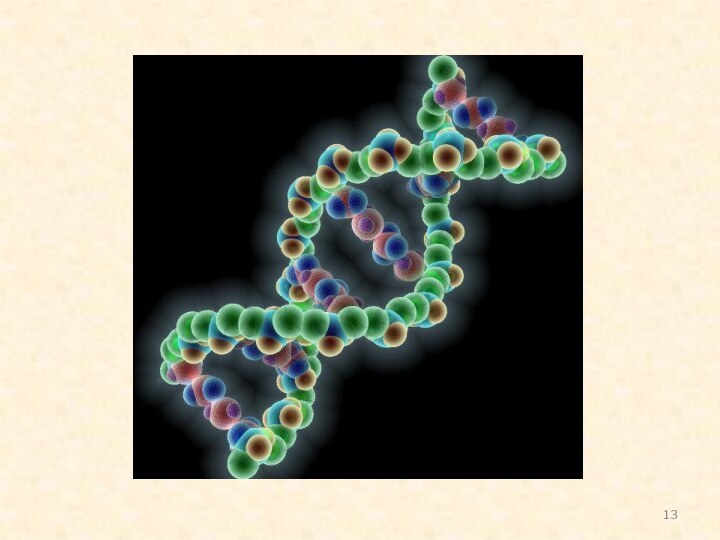Слайд 13: Безумно красива двойная спираль молекулы ДНК. Слайд 14: Многие объекты в природе обладают свойствами фрактала. Например, такие растения, как брокколи, лист папоротника, алое и другие. https://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB Слайд 15: Раковины многих молюсков близки по форме к логарифмической спирали. Отцом этой спирали, по всей справедливости, является Якоб Бернулли, который ее полностью изучил и которого она настолько заворожила, что он просил изобразить ее на его могиле. http://hijos.ru/2011/04/13/yakob-bernulli-logarifmicheskaya-spiral Слайд 16: Бывший лазерный физик Том Беддард создал невероятные произведения искусства, которые демонстрируют красоту и сложность фракталов. http://ochendaje.livejournal.com/483849.html Слайд 17: Объемная геометрическая сборная модель. Слайд 18: В эпоху Возрождения в живописи возникло новое направление – реализм, которое позволило передать трехмерность реального мира. Пьерро делла Франческа, Лука Пачолли и Леонардо да Винчи применяли новаторский метод перспективы, использовав многогранники в качестве моделей. Леонардо да Винчи первым изобразил многогранники с прозрачными гранями, так, что зрителю были видны их ребра, расположенные сзади. Наиболее удивительны работы Фра Джованни да Верона, выполненные в начале 16 в., одна из которых представлена на слайде. http://www.graphicine.com/a-picture-is-worth Слайд 19: Удивительной красоты вышитый мячик, по форме представляющий собой усеченный кубооктаэдр. Слайд 20: Вышитые кубики также очень красивы. Не менее популярное занятие среди вышивальщиц - вышивка сэмплеров, содержащих как простые растительные и животные узоры, так и геометрические формы, например, восьмиугольники. Ими особенно богата вышивка Квакеров. С 17 века в среде этого религиозного общества девочек обучали такой вышивке. Существует мнение, что через вышивку равнобедренных треугольников, шестиугольников и параллелограммов девочек обучали геометрии, которая не входила для них в школьную программу. http://www.justnan.com/jn273-miss-kitty's-pin-cube.html http://irinapetrenko.blogspot.ru/2013/09/blog-post_7.html

архитектуры, наделяя ее, согласно классической триаде Витрувия, «пользой, прочностью

и красотой». Самые разнообразные геометрические формы можно встретить в образцах русского зодчества. Рисунок 19 века. http://www.liveinternet.ru/community/1726655/post267855217 Слайд 22: Форма купола в русском храмовом зодчестве имеет символический смысл. Форма луковицы — символ пламени свечи. Золото — символ небесной славы. Число глав так же символично и может доходить до тридцати трех. Замысловатая форма и яркая раскраска куполов на храме Василия Блаженного не может оставить равнодушным ни одного человека. Слайд 23: В основе этой конструкции - модель додекаэдра. Слайд 24: Геометрические скульптуры Джорджа У. Харда. http://www.georgehart.com/sculpture/sculpture.html Слайд 25: Кристаллы - самые красивые многогранники. Драгоценные камни не могут оставить равнодушным ни одно женское сердце. Кристаллы алмаза по форме близки к октаэдрам. В истории огранки алмазов важную роль сыграл Марсель Толковский, который в 1919 году написал книгу «Конструирование бриллианта». С помощью тригонометрических расчетов он определил оптимальную форму и пропорции бриллианта, при которой достигается максимальная яркость и блеск камня. Однако многогранники используются не только при огранке бриллиантов, но и при изготовлении более скромных украшений. Слайд 26: Венгерский писатель и преподаватель архитектуры Эрнё Рубик в 1974 году придумал самую популярную кубическую головоломку всех времен. Решение задачи стало предметом различных соревнований и любопытных математических исследований. Разновидности кубика Рубика – правильные и полуправильные многогранники. Они уже давно стали предметом коллекционирования. Правила их сборки те же, но сложность из-за необычной формы выше. Слайд 27: Многогранники можно связать крючком. 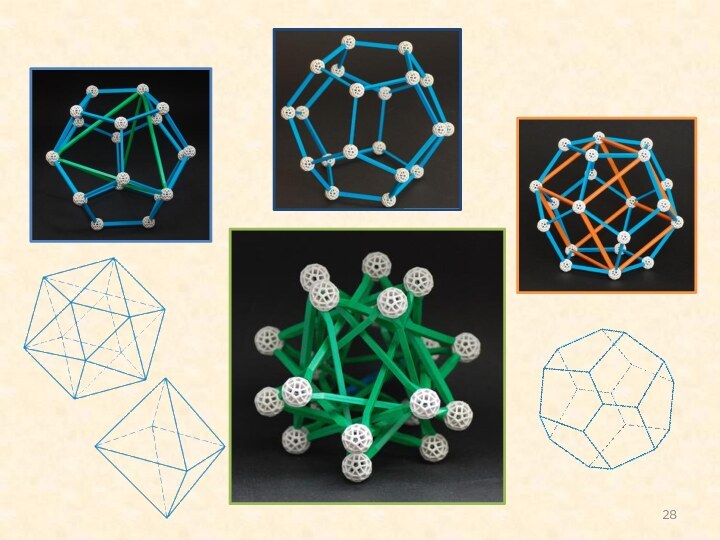http://lifemadecreations.blogspot.ru/2014/05/crochet-dodecahedron.html Слайд 28: Модели многогранников из конструктора. «Почему мы не рассматриваем многогранники сами по себе, не наслаждаемся их красотой и удивительными свойствами?» Марждори Сенешаль, американский математик и историк науки, профессор. http://www.matematicasvisuales.com/english/html/geometry/resources/zome.html Слайд 29: Новогодние игрушки из бусин и бисера. Слайд 30: Лоскутные мячики под новогодней елкой. Сшиты по выкройкам многогранников. http://ta-lulla.livejournal.com/36355.html