- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Показательная функция (обобщающее занятие)
Содержание
- 2. Содержание
- 3. «Нет никакой области знаний, в которую бы
- 4. История развития понятия «функция»Идея функциональной зависимости восходит
- 5. История развития понятия «функция»Само слово “функция” (от
- 6. Биографические сведения о Леонарде ЭйлереЛеонард Эйлер родился
- 7. Биографические сведения о Леонарде ЭйлереВ 30-е годы
- 8. ЭкспонентаНарисуем несколько графиков функций, y=ax, изменяя а:
- 9. ЭкспонентаЧисло e — математическая константа, иррациональное и трансцендентное
- 10. ЭкспонентаСаму константу впервые вычислил швейцарский математик Якоб Бернулли в
- 11. «Некоторые наиболее часто встречающиеся виды трансцендентных функций,
- 12. Применение показательной функцииВ биологии, экологии и медицине
- 13. Задача:Культуре из 100 бактерий предоставлена возможность размножаться
- 14. Применение показательной функции в физикеПроцесс изменения температуры
- 15. Задача:Период полураспада плутония равен 140 суткам. Сколько
- 16. Применение показательной функции в экономикеВ финансовой математике
- 17. Задача:На вклад с начислением сложных процентов помещены
- 18. «В математике следует помнить не формулы, а процессы мышления» Василий Петрович Ермаков, русский математик (1845-1922) Викторина
- 19. 1. Через какую точку проходят графики всех показательных функций?М (1;0)
- 20. 2. С помощью какого преобразования плоскости можно
- 21. y = 3(x-1)y = 3 x -
- 22. 4. Какая из следующих функций является возрастающей?y
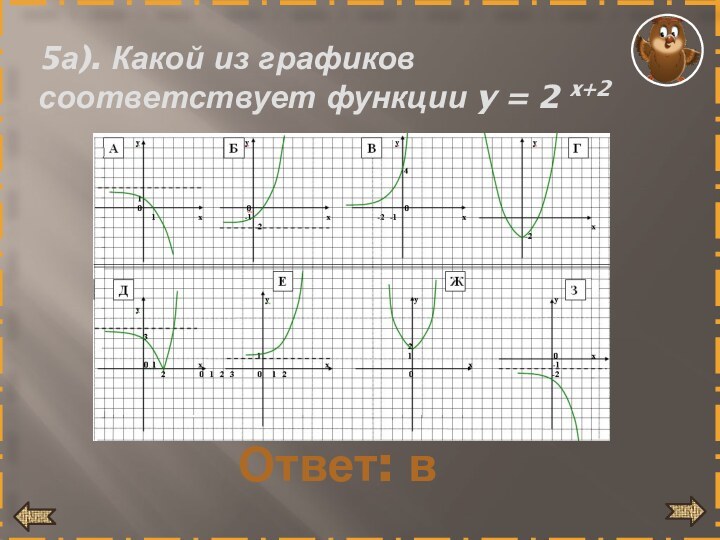
- 23. 5а). Какой из графиков соответствует функции y = 2 x+2Ответ: в
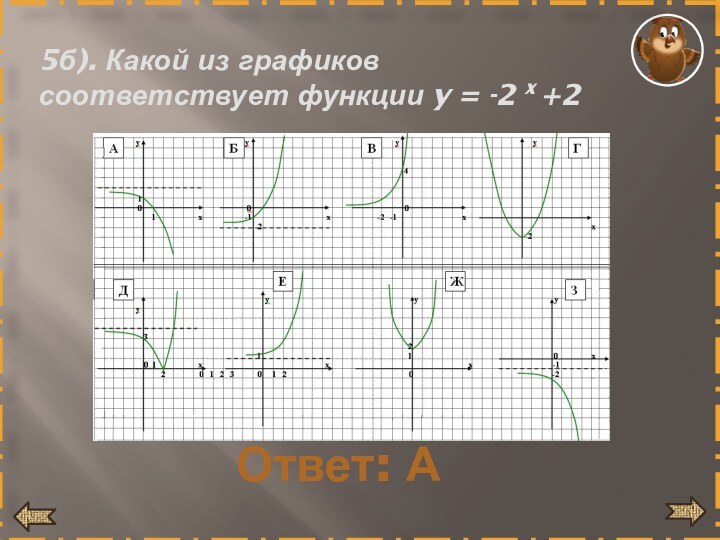
- 24. 5б). Какой из графиков соответствует функции y = -2 x +2Ответ: А
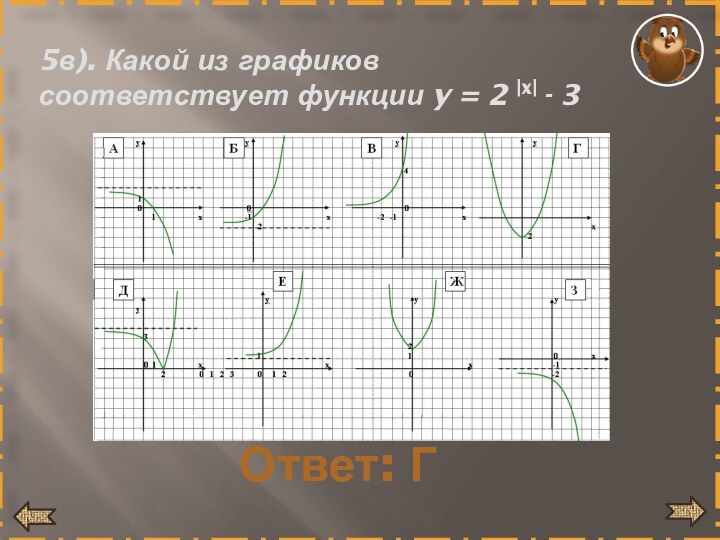
- 25. 5в). Какой из графиков соответствует функции y = 2 x - 3Ответ: Г
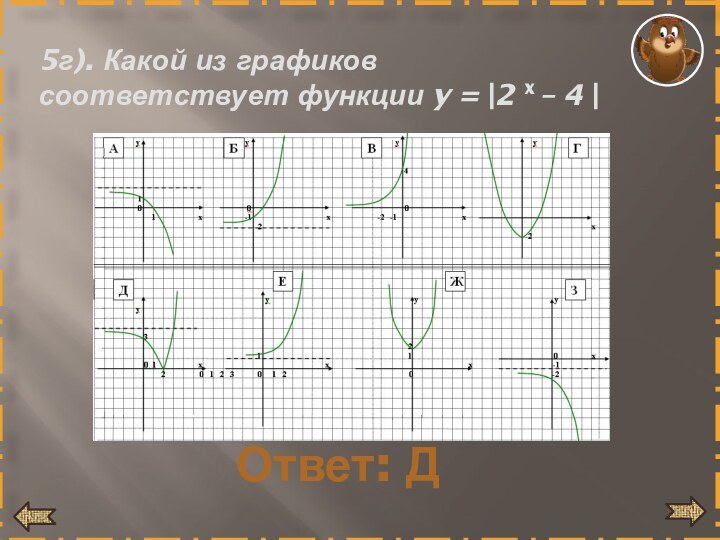
- 26. 5г). Какой из графиков соответствует функции y = 2 x – 4 Ответ: Д
- 27. 6. В каком случае первое число меньше
- 28. 7. Сколько точек пересечения имеют графики функций у = х1/2 и у = 2х?Ни одной
- 29. 8. Показательная функция не является ни четной, ни нечетной.
- 30. 0,2 (x+0,5) = (0,04 x) /25102 x
- 31. 10. Неравенства 0,5 7-х 1 и 7 – х 0 не являются равносильными
- 32. 11. Какой промежуток является решением неравенства: (1/3) x 93; +)-2; 0)(-; -2(-; 2-2; +)
- 33. Домашнее заданиеАлимов Ш.А. и др. Алгебра и
- 34. Скачать презентацию
- 35. Похожие презентации
Содержание





























Слайд 4
История развития понятия «функция»
Идея функциональной зависимости восходит к
древности.
Так, вавилонские ученые (4-5тыс.лет назад) установили, что площадь
круга является функцией от его радиуса посредством нахождения приближенной формулы: S=3r2. Примерами табличного задания функции могут служить астрономические таблицы вавилонян, а примерами словесного задания функции – античные определения конических сечений. Начиная лишь с 17 века понятие функции явно и вполне сознательно применяется.
Франсуа Виет и Рене Декарт разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Тем самым появилась возможность записывать общие формулы.
В своей “Геометрии” в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы.
В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени.
Слайд 5
История развития понятия «функция»
Само слово “функция” (от латинского
functio - совершение, выполнение) впервые было употреблено немецким математиком
Лейбницем в 1673г. в письме к Гюйгенсу, а в печати – с 1694 года. В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748). Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Леонард Эйлер.Эйлер же впервые ясно определил большинство элементарных функций, в том числе показательную функцию.
Слайд 6
Биографические сведения о Леонарде Эйлере
Леонард Эйлер родился в
Базеле (Швейцария) 15 апреля 1707 года в семье пастора
и провел детство в близлежащем селении, где его отец имел приход. Здесь Леонард получил начальное образование, наложившее глубокий отпечаток на всю его последующую жизнь. После окончания гимназии в 13 лет Эйлер поступил в Базельский университет, через три года окончил философский факультет и по настоянию отца записался на теологический.Проявив свои математические таланты, Эйлер привлек к себе внимание Иоганна Бернулли. Профессор стал руководить самостоятельными занятиями юноши.
В 1725 году Леонард Эйлер выразил желание сопровождать сыновей своего учителя в Россию, куда они были приглашены в Петербургскую академию наук. На следующий год он получил приглашение и сам. Весной 1727 года Эйлер прибыл в Петербург и был зачислен адъюнктом по кафедре высшей математики, а с 1731 года стал академиком (профессором).
В один из последних дней 1733 года 26-летний Леонард Эйлер женился на своей ровеснице Катарине, дочери швейцарского живописца. Молодожены приобрели дом на набережной Невы, где и поселились. В семье Эйлера родились 13 детей, но выжили 3 сына и 2 дочери.
Эйлер отличался феноменальной работоспособностью. По отзывам современников, для него жить означало заниматься математикой. За первый период пребывания в России он написал более 90 крупных научных работ.
Слайд 7
Биографические сведения о Леонарде Эйлере
В 30-е годы 18
века Эйлер становится известен в Европе. После смерти императрицы
Анны Леопольдовны Петербургская академия наук приходит в запустение, и Эйлер принимает предложение прусского короля Фридриха занять должность директора Математического департамента Берлинской академии. В Берлине Эйлер провел 25 лет и издал около 260 работ. Помимо математики он занимался многими практическими делами, включая лотереи, чеканку монет, прокладку водопровода и организацию пенсионного обеспечения.Все эти годы он помогал Петербургской академии: участвовал в публикациях, редактировал математические отделы русских журналов, приобретал для Петербурга книги и инструменты. На квартире Эйлера на полном пансионе годами жили молодые русские ученые, командированные на стажировку. Известно об оживленной переписке Эйлера с Ломоносовыми.
Первое время Эйлера встречают в Берлине доброжелательно, однако в дальнейшем отношения с королем не складываются – Фридрих находит великого математика невыносимо скучным, совершенно не светским.
В 1762 году на русский престол вступила Екатерина II. Она предложила Эйлеру вернуться в Россию. 60-летний Эйлер с семьей прибыл в Россию, где жил и плодотворно работал до самой смерти.
Слайд 8
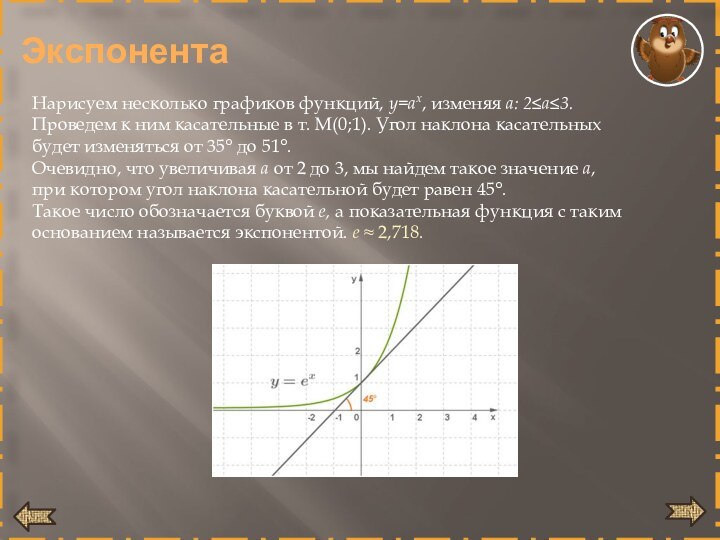
Экспонента
Нарисуем несколько графиков функций, y=ax, изменяя а: 2≤а≤3.
Проведем
к ним касательные в т. М(0;1). Угол наклона касательных
будет изменяться от 35 до 51. Очевидно, что увеличивая а от 2 до 3, мы найдем такое значение а, при котором угол наклона касательной будет равен 45. Такое число обозначается буквой е, а показательная функция с таким основанием называется экспонентой. е ≈ 2,718.
Слайд 9
Экспонента
Число e — математическая константа, иррациональное и трансцендентное число.
Приблизительно равно 2,71828.
Число е можно представить как сумму:
Число
е является пределом последовательности чисел:xn = (1+1/n)n
xn = {2; 2,25; 2,37; 2,44; …}
Слайд 10
Экспонента
Саму константу впервые вычислил швейцарский математик Якоб Бернулли в ходе
решения задачи о предельной величине процентного дохода. Бернулли показал, что
если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел, равный е.Символ e для обозначения этого числа был введен в 1731 Л.Эйлером.
Слайд 11 «Некоторые наиболее часто встречающиеся виды трансцендентных функций, прежде
всего показательные, открывают доступ ко многим исследованиям» Леонард Эйлер,
швейцарский математик (1707-1783)
Слайд 12
Применение показательной функции
В биологии, экологии и медицине —
Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое
количество пищи) живые организмы размножались бы по закону показательной функции. Например: одна комнатная муха может за лето произвести 8 1014 особей потомства. По такому же принципу распространились завезённые в Австралию кролики, которые стали экологической катастрофой для этого уникального региона. Ещё по этому закону возрастает количество клеток гемоглобина в организме человека, который потерял много крови.Закон органического затухания: подобен размножению, происходит с той же скоростью и по тем же условиям, но происходит в обратную сторону.
Закон выравнивания: он тоже описывается показательной функцией и присутствует при таких процессах, как разрушение адреналина в крови и уменьшение количества радиоактивных веществ, выводимых почками.
Все эти процессы подчиняются одному закону: N = N0ekt
В демографии – рост народонаселения аналогичен закону органического размножения в биологии.
Слайд 13
Задача:
Культуре из 100 бактерий предоставлена возможность размножаться при
благоприятных условиях. Через 12 часов число бактерий достигло 500.Сколько
бактерий будет через двое суток после начала опыта?
Слайд 14
Применение показательной функции в физике
Процесс изменения температуры чайника
при кипении выражается формулой: T=T0+(100-T0)e-kt - это пример процесса
выравнивания, который в физике также можно наблюдать при включении и выключении электрических цепей, и при падении тела с парашютом.Сила света I определяется по формуле: I = I0e-ks , где s – толщина слоя, k – коэффициент характеризующий мутную среду. При прохождении света через мутную среду каждый слой этой среды поглощает строго определенную часть падающего на него света.
Барометрическая формула – давление воздуха убывает с высотой (при постоянной температуре) по закону p=p0e-h/H, где p0 – давление на уровне моря, р – давление на высоте h, H – некоторая константа, зависящая от температуры.
Радиоактивный распад – Когда радиоактивное вещество распадается, его количество уменьшается, через некоторое время остается половина от первоначального вещества. Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)-t/t0 , где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e-kt, используя данную формулу ученые рассчитали возраст Земли.
Слайд 15
Задача:
Период полураспада плутония равен 140 суткам. Сколько плутония
останется через 10 лет, если его начальная масса равна
8г ?
Слайд 16
Применение показательной функции в экономике
В финансовой математике увеличение
суммы денег в результате начисления сложных процентов определяется формулой:
FV=PV(1+j/m)mnгде PV – исходная сумма денег FV – наращенная сумма денег n – число лет, соответствующее сроку финансовой операции j – ставка процентов за год m – число периодов начисления в году
В практических банковских расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированный промежуток времени (год, полугодие, квартал и т.д.). В некоторых случаях возникает необходимость в применении непрерывных процентов. Сумма денег при непрерывном начислении процентов увеличивается в соответствии с формулой S(t)=S0 e δt,
где S0 – начальная сумма денег.
В этой формуле величина δ характеризует скорость роста суммы. Ее называют силой роста, или силой процента. Она равна скорости относительного прироста суммы, т. е. равна относительному приросту суммы за бесконечно малый промежуток времени.
Слайд 17
Задача:
На вклад с начислением сложных процентов помещены 10
000 р. Определить наращение суммы вклада через 2 года,
если проценты начисляются ежеквартально из расчета 8 % годовых.Слайд 18 «В математике следует помнить не формулы, а
процессы мышления»
Василий Петрович Ермаков, русский математик (1845-1922)
Викторина
Слайд 20 2. С помощью какого преобразования плоскости можно получить
график функции у = (0,5)х из графика функции у
= 2х?Симметрия относительно оси Оу
Слайд 21
y = 3(x-1)
y = 3 x - 1
y
= - 3 x
y = 1 + 3 x
y
= 3 xСимметрия относительно оси Ох
Нижняя полуплоскость отображается симметрично относительно оси Ох
Сдвиг вправо на 1
Сдвиг вверх на 1
Сдвиг вниз на 1
3. Сопоставьте функцию и преобразование, с помощью которого можно получить ее график из графика функции y = 3x
Слайд 22
4. Какая из следующих функций является возрастающей?
y =
(/5) x
y = (е/)x
y = 0,2 x
y = (1/e)
xy = (1/0,2) x
Слайд 27
6. В каком случае первое число меньше второго?
10
и 10 е
(1/2) 2 и (1/2) 4
3,1 10
и 3,1 31(1/е) и 1 е
0,3 10 и 0,3 3
Слайд 30
0,2 (x+0,5) = (0,04 x) /25
102 x –
3·10 x – 4 = 0
5 (3x+1) =
26х+2(3/4)x + 1 = (5/4) x
(1/3) x = 3x2
Замена переменной
Графический
Приведение к одному показателю
Использование
свойств степеней
Использование свойства монотонности
9. Сопоставьте уравнение и метод его решения
Слайд 32 11. Какой промежуток является решением неравенства: (1/3) x
9
3; +)
-2; 0)
(-; -2
(-; 2
-2; +)
Слайд 33
Домашнее задание
Алимов Ш.А. и др. Алгебра и начала
анализа. 10-11 кл. - Упр. к главе 3, «Проверь
себя»Составить синквейн к словам «функция», «график», «экспонента», «степень»








![Проект урока обучение грамоте 1 класс, тема Согласные звуки [м], [м’], буквы М, м.](/img/tmb/13/1211511/6a11e351f2ae0494b0ee96a4c5f1a7c8-210x.jpg)




















