быть подвергнут преобразованиям:
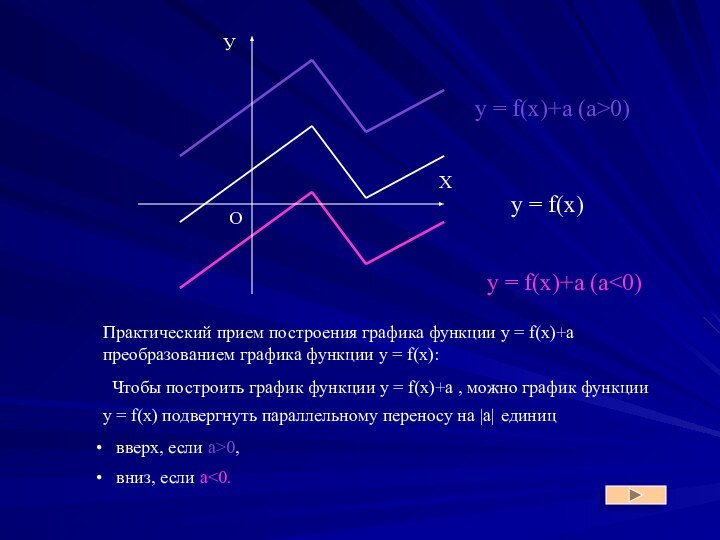
y = f(x)+a
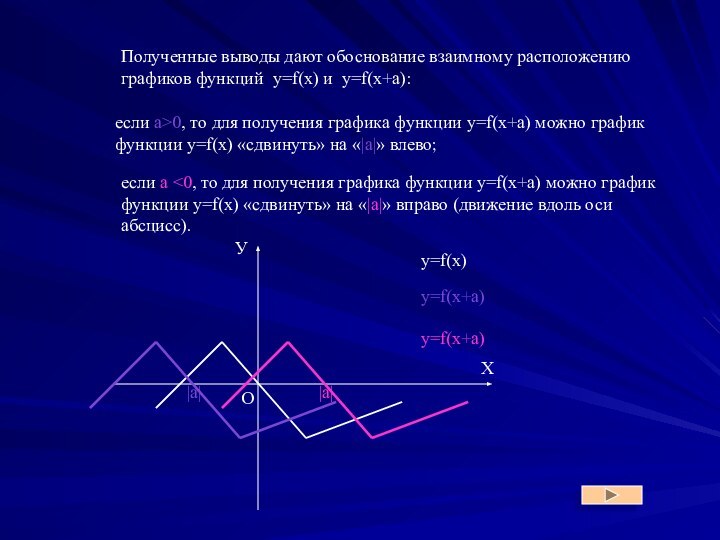
y = f(x+a)
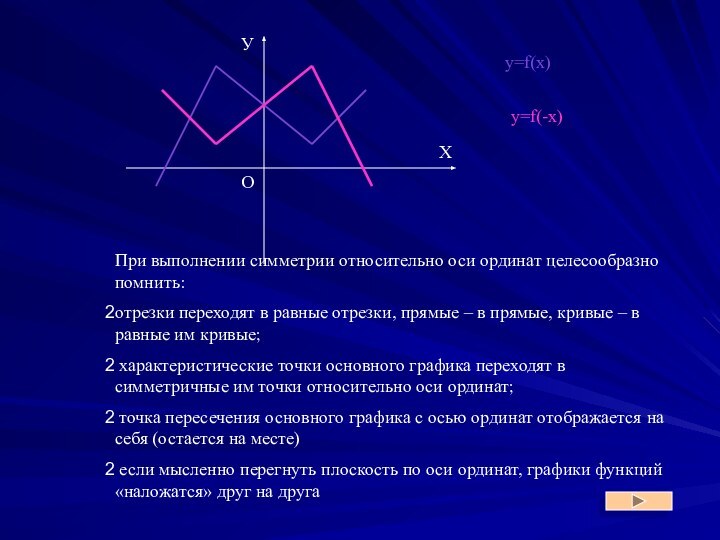
y = - y = - y = - f(x)y = f(-x)
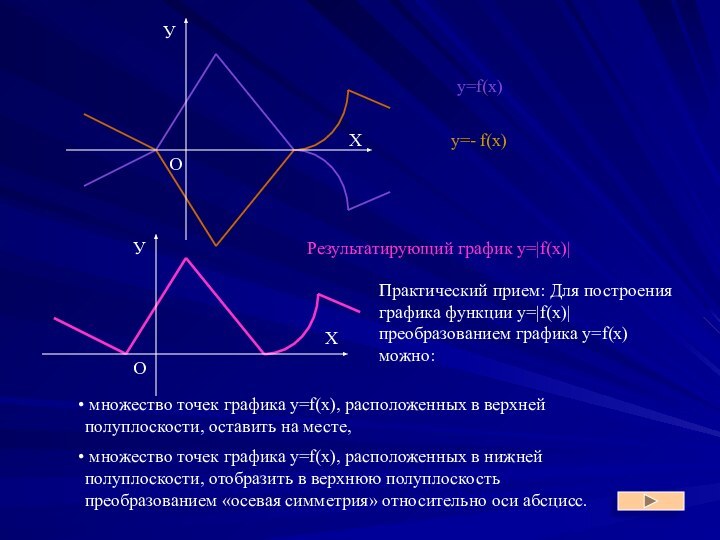
y = |f(x)|
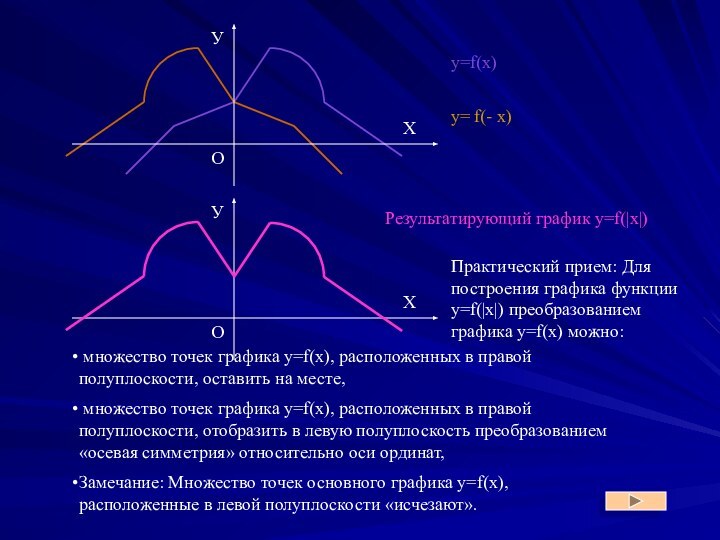
y = f(|x|)
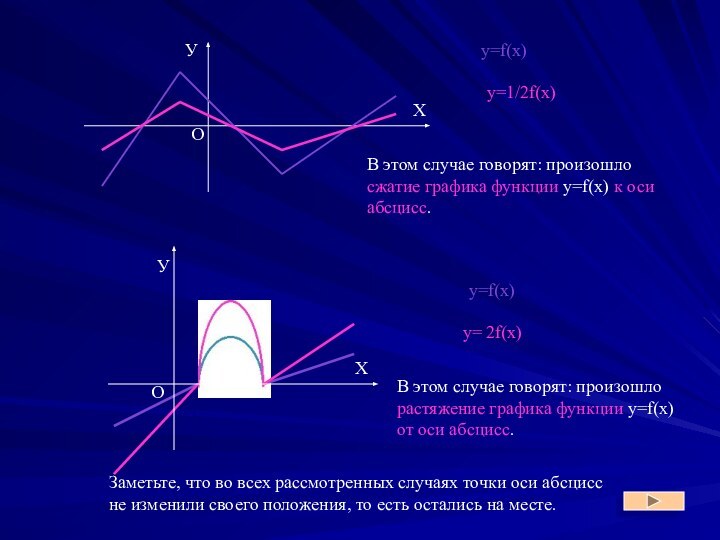
y = аf(x)
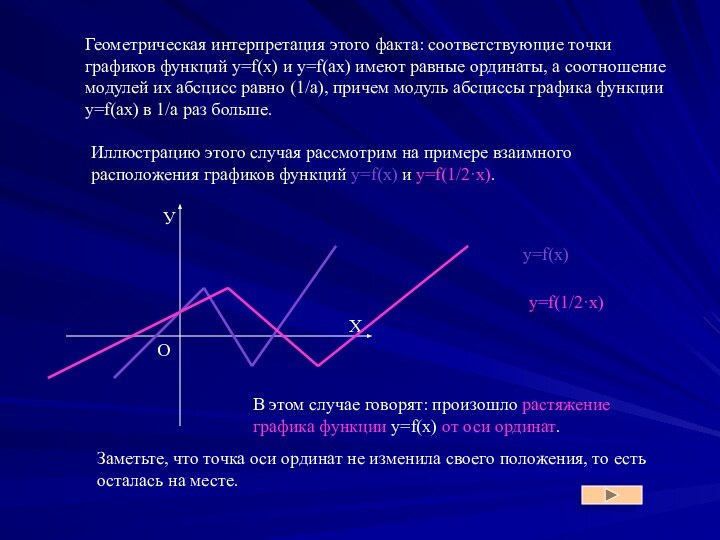
y = f(аx)
комбинации преобразований
Примечание: После рассмотрения каждого из выделенных видов
преобразований Вы можете вернуться на этой слайд,
воспользовавшись гиперссылкой «Возврат».