Презентация на тему Урок Координатная плоскость

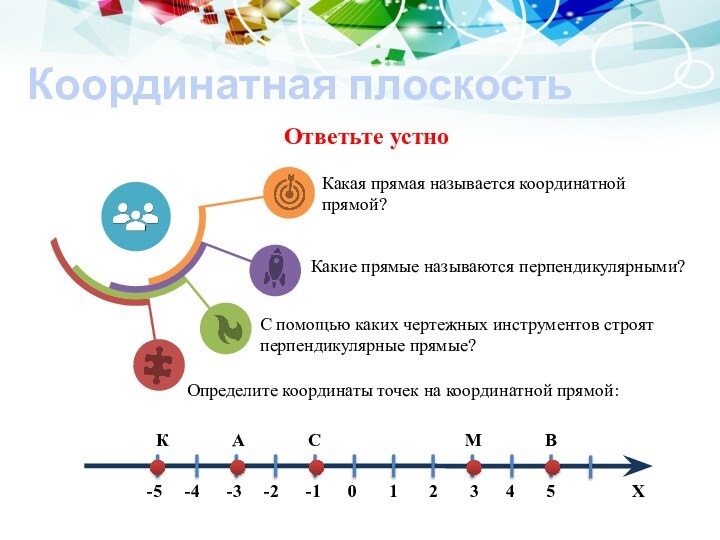
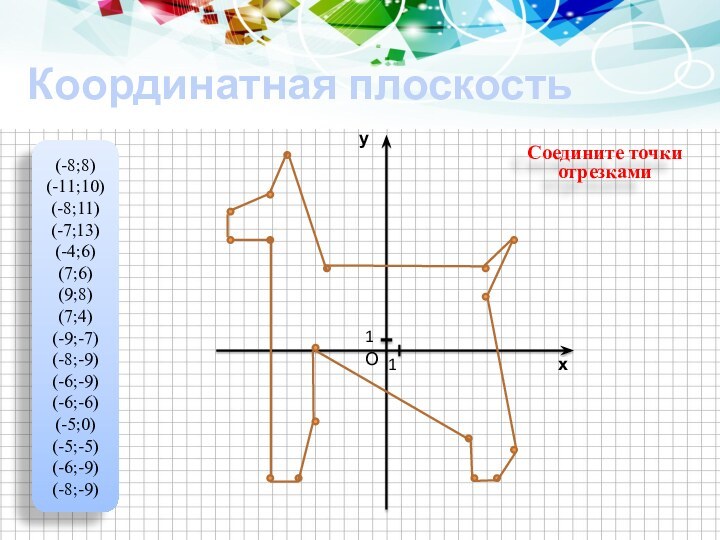
“координатная плоскость”, “система координат”, “прямоугольная система координат”, их использование

в практических целях; научить учащихся ориентироваться на координатной плоскости, находить координаты заданных точек, и по заданным координатам точки определять ее положение на координатной плоскости;

Развивающая: развивать познавательную активность, творческие способности учащихся;

Воспитательная: воспитание интереса к предмету с привлечением мультимедийных возможностей.

Цели урока

точек на координатной прямой:
Какие прямые называются перпендикулярными?
С помощью каких

чертежных инструментов строят перпендикулярные прямые?

мы ищем свой ряд, затем своё место.

что 10 ряд 2 место
10 ряд
2 место
2 ряд
10 место

свой вагон, затем номер своего места.

составил первый в Европе звёздный каталог, включивший точные значения

координат около тысячи звёзд.

параллели и меридианы составляют градусную сетку.

неизвестной им карте соперника. Если у соперника по этим

координатам имеется корабль, то корабль или его часть «топится», а попавший получает право сделать ещё один ход.

фигурами на 64-клеточной доске для двух соперников, сочетающая в

себе элементы искусства (в части шахматной композиции), науки и спорта.

Игра происходит на доске, поделенной на равные квадратные клетки, или поля. Размер доски — 8×8 клеток. Вертикальные ряды полей (вертикали) обозначаются латинскими буквами от а до h слева направо, горизонтальные ряды (горизонтали) — цифрами от 1 до 8 снизу вверх; каждое поле обозначается сочетанием соответствующих буквы и цифры.

знаний о географии всего известного античным народам мира. В

своем трактате Птолемей заложил основы математической географии и картографии. Опубликовал координаты восьми тысяч пунктов.

Декарт в своей работе «Геометрия» в 1637 году. Поэтому

прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии.

степеней. Он дал общий способ для проведения касательных к

произвольной алгебраической кривой. В «Трактате о квадратурах» (1658) Ферма показал, как найти площадь под гиперболами различных степеней, распространив формулу интегрирования степени даже на случаи дробных и отрицательных показателей.

Лейбниц, независимо от Ньютона, создал математический анализ — дифференциальное и

интегральное исчисления, основанные на бесконечно малых.
Лейбниц создал комбинаторику как науку.
Он заложил основы математической логики.
Описал двоичную систему счисления с цифрами 0 и 1.
В механике ввёл понятие «живой силы» (прообраз современного понятия кинетической энергии) и сформулировал закон сохранения энергии.

состоит фигура?

система координат.
Координаты– это пара чисел точки (х; у)
Чтобы расположить

точку (х; у) на координатной плоскости необходимо:
1) сначала пройти по оси Х (абсцисс) влево или вправо на х «rлеточек»
2) потом подняться или опуститься на у «клеточек» по оси У (оси ординат)

Чтобы определить координаты точки надо:
1) опустить перпендикуляр на ось Х (ось абсцисс) и записать х
2) опустить перпендикуляр на ось У (ось ординат) и записать у

характеристик.
… точки A называется координата этой точки на оси

Y’Y в прямоугольной системе координат.

… координат — особая точка, обозначаемая буквой О, которая используется как точка отсчёта для всех остальных точек.

Наука о структурах, порядке и отношениях, сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

… координат — способ определять положение точки или тела с помощью чисел или других символов.

Основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

Рене …

… Ферма

Т

О

Ч

К

А

О

Р

Д

И

Н

А

А

Т

А

М

Е

М

А

И

К

А

Т

Т

Ч

И

С

Л

О

М

Е

Т

О

Д

П

Ь

Е

Р

Д

Е

К

А

Р

Т

Н

А

Ч

А

Л

О

и неясности
Было трудно, ничего не понял
Рефлексия