Часть 1
Практикум.Расстояние в пространстве.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторно-координатный метод решения задач
Содержание
- 2. Векторно-координатный метод решения стереометрических задач
- 3. Расстояние от точки до прямой
- 4. Расстояние от точки до прямой
- 5. Расстояние от точки до плоскости
- 6. Расстояние от точки до плоскости
- 7. Расстояние от точки до плоскости
- 8. Расстояние между прямыми
- 9. Расстояние между прямыми
- 10. Векторно-координатный метод решения стереометрических задачЧасть 2Углы в пространстве
- 11. Углы в пространстве
- 12. Угол между прямыми
- 13. Угол между прямой и плоскостью
- 14. Угол между прямой и плоскостью
- 15. Угол между прямой и плоскостью
- 16. Угол между плоскостями
- 17. Угол между плоскостями
- 18. Угол между плоскостями
- 19. Угол между плоскостями
- 20. Векторно-координатный метод решения стереометрических задачЧасть 3Практикум. Вектор нормали и рациональные методы решения задач.
- 21. Угол между плоскостями•Решение.Рассмотрим более простое решение.
- 22. Угол между плоскостями•60
- 23. Угол между плоскостями
- 24. Угол между плоскостями
- 25. Угол между прямой и плоскостьюАBСS ОКFLNРешение.Построим фигуру.Точка
- 26. Угол между прямой и плоскостью
- 27. Угол между прямой и плоскостьюРешим задачу другим
- 28. Угол между прямой и плоскостью
- 29. Угол между прямой и плоскостьюВ этом решении
- 30. Скачать презентацию
- 31. Похожие презентации
Векторно-координатный метод решения стереометрических задач Часть 1 Практикум. Расстояние в пространстве.
Слайд 2
Векторно-координатный метод решения стереометрических задач
Часть 1
Практикум.Расстояние в пространстве.
Слайд 20
Векторно-координатный метод решения стереометрических задач
Часть 3
Практикум.
Вектор нормали
и рациональные методы решения задач.
Слайд 25
Угол между прямой и плоскостью
А
B
С
S
О
К
F
L
N
Решение.
Построим фигуру.
Точка О
– точка пересечения медиан.
Опустим FN ⊥(АВС).
FК – наклонная к
(АВС), FN – ее проекция. Следовательно, угол FKN искомый угол.
Слайд 27
Угол между прямой и плоскостью
Решим задачу другим способом.
Введем
систему координат.
Найдем координаты точек :
А, В, С, К и
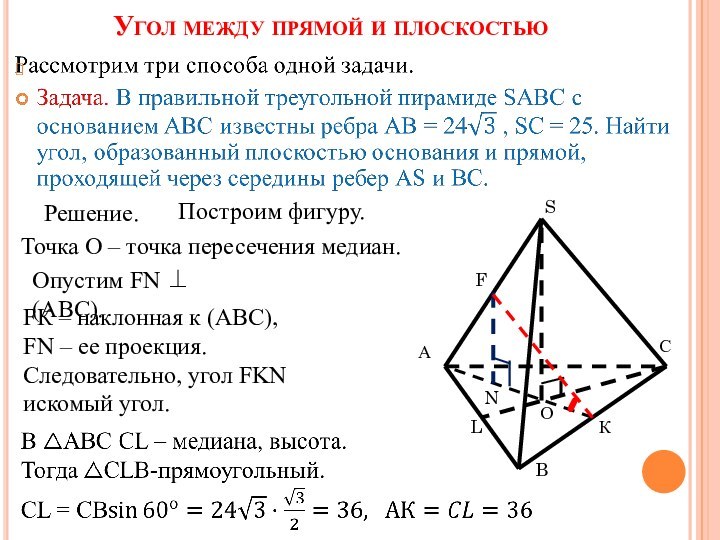
F.А
B
С
S
F
N
О
L
К
0
36
6
18
7
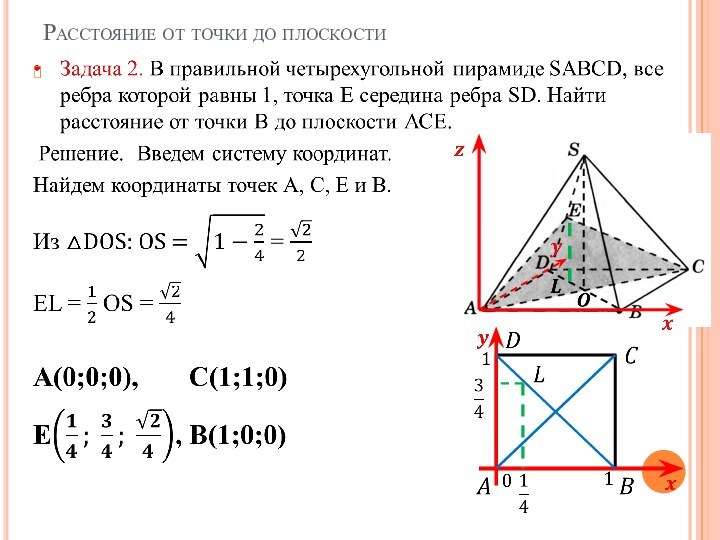
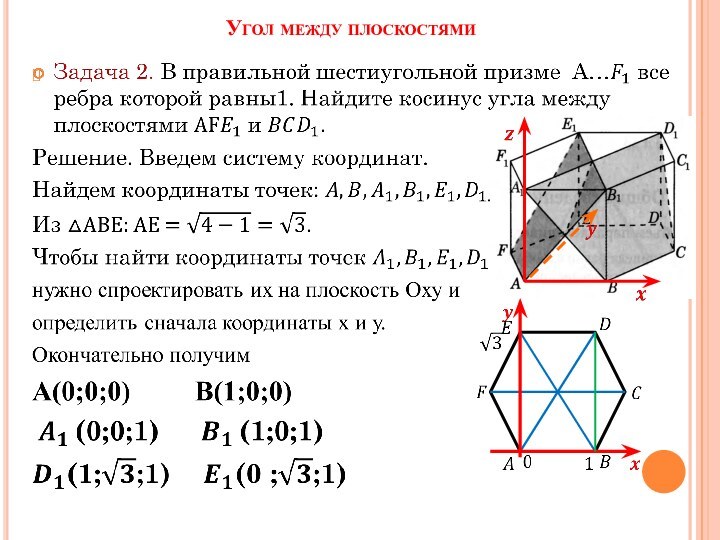
А(0; 0; 0),
Слайд 29
Угол между прямой и плоскостью
В этом решении мы
