Слайд 2
Актуальность
Нанотехнологии и нанонауки, многофункциональные материалы, основанные на
новых знаниях и предназначенные для новых производственных процессов и
устройств.
Промышленность и общество могут извлечь пользу из новых знаний посредством разработки новых продуктов и технологических процессов.
Необходима согласованность национальных исследовательских программ и инвестиций. Это должно гарантировать обеспечение страны командами и соответствующей инфраструктурой, нацеленными на решение актуальных задач.
Слайд 3
Прошлое и настоящее схемотехники
Слайд 4
Настоящее и будущее схемотехники
Слайд 5
Новизна
Представлен новый подход к пониманию и освоению свойств
трехмерных интегральных схем.
Разработана соответствующая подходу схемотехника.
Разработано программное обеспечение,
позволяющее синтезировать новые интегральные структуры, а также «совершать экскурсию» внутрь интеллектуального кристалла и «гулять» там.
Слайд 6
Теория
Разработана переходная схемотехника для 3-d СБИС.
Компонент схемотехники
- физический переход между материалами с различными свойствами.
Математические модели
интеллектуальных элементов содержат минимальное количество переходов и физических областей с различными свойствами.
Некоторые модели «совпадают» по структуре с органическими молекулами, имеющими те же логические функции.
Слайд 7
Теоретические основы переходной схемотехники (ТОПС 1)
Математической моделью функционально-интегрированного
элемента (ФИЭ) является неориентированный граф
G (X, А, Г),
где: X
= (х1, х2, …хN) – множество вершин,
А = (а1,а2,…аМ) – множество ребер.
Предикат Г является трехместным предикатом и описывается логическим высказыванием
Г (xi, ak, xj),
которое означает, что ребро aк соединяет вершины хi и xj.
Слайд 8
ТОПС 2
Элементу множества вершин хi соответствует часть интегральной
структуры
Fi
Тi
,
в которой
Тi определяет качественный состав части интегральной структуры,
Fi – элемент функционального множества.
Т = {Ti}(i=1,n) = (p,n,p+,n+,…SiO2, Al, Ga…) = П U Д U М –
множество элементов типа частей структуры (р – полупроводниковая область р-типа, n – полупроводниковая область n-типа, SiO2 – область двуокиси кремния, Аl – область алюминия, Ga – область галия и т.д.),
П – подмножество областей полупроводников, Д – подмножество областей диэлектриков, М – подмножество проводников.
Слайд 9
ТОПС 3
Функциональное множество
F = Fy U FH
состоит из
двух подмножеств:
Fy = {Fyi} = (E1,…,Ek1,I1,…,Ik2,φ1,…,φk3…)
подмножества управляющих воздействий в
виде напряжения Еi, тока Ij, света φк и
FH = {FHi} = (вх1,…,вхm,вых1,…,выхn)
подмножества назначения, задающего входные и выходные функции областям из подмножества Т, по отношению к которым определяются передаточные характеристики элементов.
N – число областей интегральной структуры, размерность элемента.
Слайд 10
ТОПС 4
Элементам множества ребер ак, аi соответствуют переходы
между различными частями интегральной структуры, выполняющие определенные функции, причем
существуют
xi, xj ( хi ≠ xj & Г (xi , ак , xj ) & Г (xj , ак , xi).
Примерами переходов – компонентов переходной схемотехники – являются:
Пi – Пj переход -
переход между полупроводниками, например, р – n переход, переход между полупроводниками р и n типа, выполняющий диодную функцию,
Пi – Дj переход -
переход между полупроводником и диэлектриком,
Пi – Мj переход -
переход между полупроводником и металлом (диод Шоттки),
переходы между прозрачными и непрозрачными слоями в оптоэлектронных элементах,
мембраны в биологических элементах и т.д,
Инциндентор Г (xi, ak, xj) означает, что область xi, имеет с областью xj физическую границу – переход ak.
Слайд 11
ТОПС 5
Графовые модели интегральных элементов могут представлять собой
деревья, а могут содержать и циклы.
цепь открытий и изобретений,
давших три последних поколения вычислительных машин, всего лишь начальные элементы таблицы оптимальных математических моделей элементов переходной (p-n) схемотехники.
Слайд 12
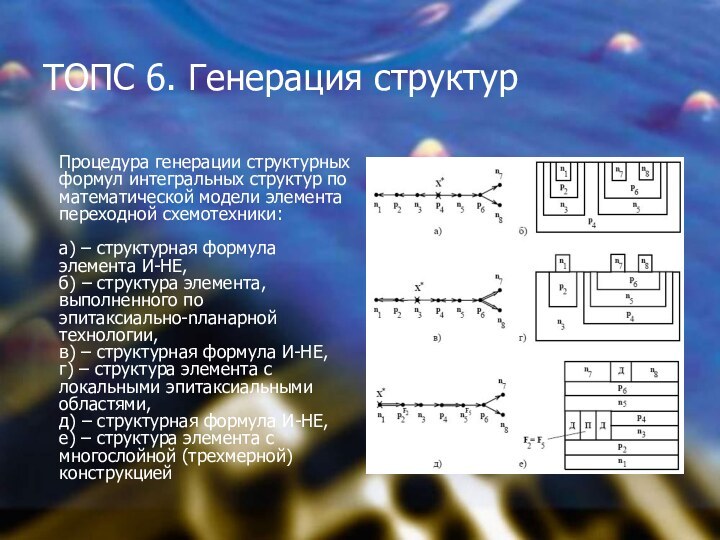
ТОПС 6. Генерация структур
Процедура генерации структурных формул интегральных
структур по математической модели элемента переходной схемотехники:
а) –
структурная формула
элемента И-НЕ,
б) – структура элемента, выполненного по эпитаксиально-nланарной технологии,
в) – структурная формула И-НЕ,
г) – структура элемента с локальными эпитаксиальными областями,
д) – структурная формула И-НЕ,
е) – структура элемента с многослойной (трехмерной) конструкцией
Слайд 13
Пример проектирования ФИЭ
а) – математическая модель (объединение двух
n-p-n транзисторов по эмиттерам и коллекторам),
б) – вертикальная
оптимальная интегральная
структура,
в) – вертикальная
структура с разбиением
вершины nвых ,
г) – горизонтальная
структура на изоляторе
Уравнение синтеза
Слайд 14
RS-триггер в переходной схемотехнике
Уравнение синтеза
RS-триггер в переходной схемотехнике:
а) – структура, б) – топология
Слайд 15
N-разрядный регистр на RS-триггерах
в переходной схемотехнике
а) –
уравнение синтеза,
б) – ДНК,
в) – интегральная структура,
г) – топология
одного разряда
Слайд 16
Биочипы (подобие углеродной и кремниевой переходных схемотехник)
На рисунке
показан синтез комплиментарной цепи ДНК из нуклеотидов, модели которых
удивительно похожи на математические модели триггеров в переходной схемотехнике.
Слайд 17
Программное обеспечение (ПО 1)
SGenerator –
генерация 2-d интегральной структуры
по математической модели ФИЭ
Слайд 18
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 1)
Слайд 19
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 2)
Слайд 20
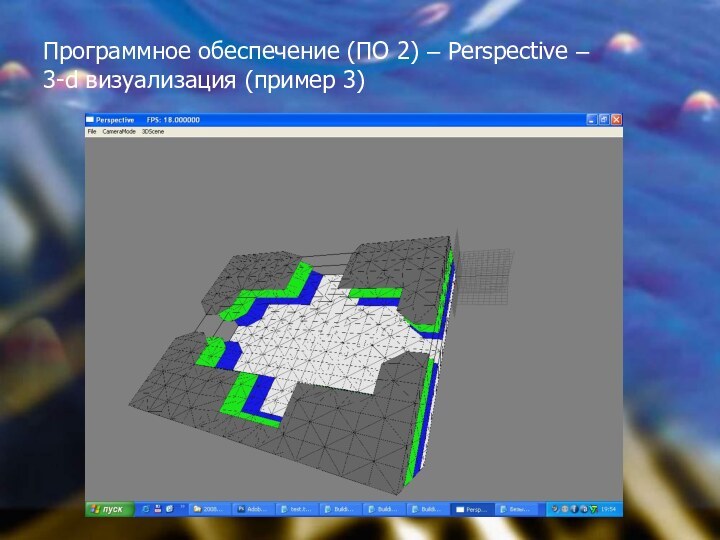
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 3)
Слайд 21
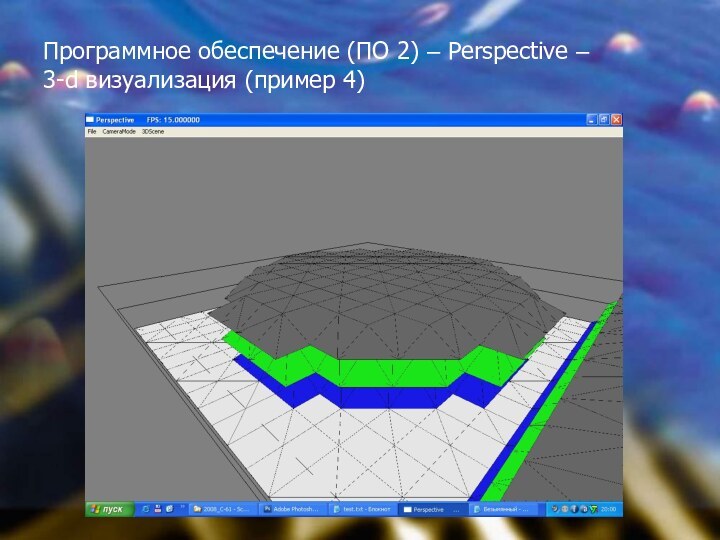
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 4)
Слайд 22
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 5)
Слайд 23
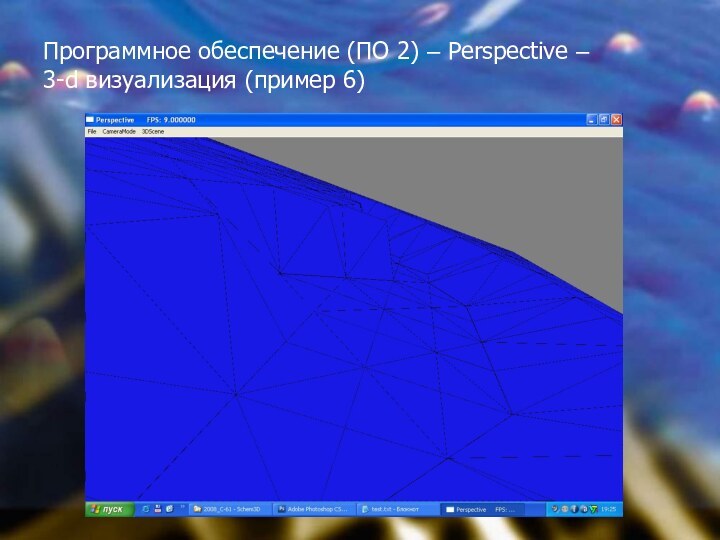
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 6)
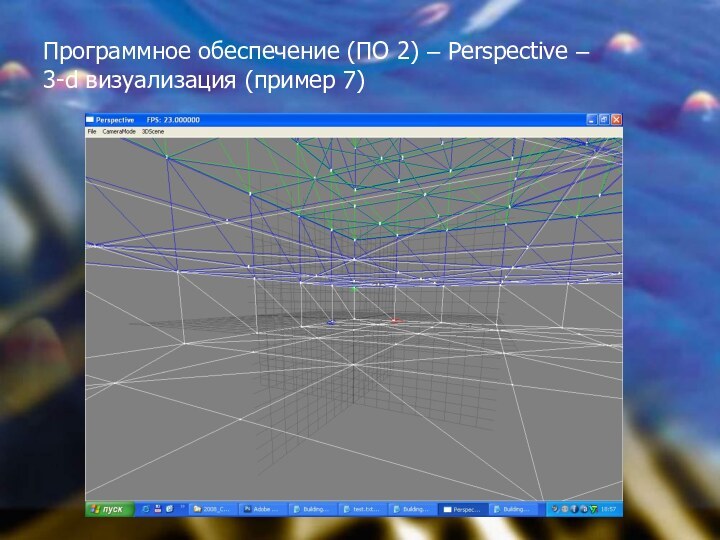
Слайд 24
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 7)
Слайд 25
Программное обеспечение (ПО 2) – Perspective –
3-d
визуализация (пример 8)
Слайд 26
Результаты
Система оптимальных математических моделей интеллектуальных элементов различной степени
сложности для 3-d СБИС.
Моделирующее программное обеспечение.
Побочный культурологический эффект:
3-d технологии в интернете (3-d сайты)
http://nadin.miem.edu.ru/my_img/3d_room/3d_p_1_1.html
Слайд 27
Обучение
Разработан учебный курс,
включающий:
курс лекций,
практикум по компьютерному
моделированию,
тестирование на
сайте
http://testing.miem.edu.ru
методические материалы
Слайд 28
Дополнительная литература
Трубочкина Н.К. Синтез на ЭВМ функционально-интегрированных элементов.
Вопросы радиоэлектроники, сер. Технология производства и оборудование, вып.1, 1985,
с.20.
Трубочкина Н.К. Логические элементы статических БИС. М: МИЭМ, 1987.
Трубочкина Н.К. Машинное моделирование функционально-интегрированных элементов. Учебное пособие. М.: МИЭМ, 1989.
Трубочкина Н.К., Мурашев В.Н., Петросян Ю.А., Алексеев А.Е. Функциональная интеграция. Концепция. Электронная промышленность, 2000, № 4, с.49-70.
Трубочкина Н.К., Мурашев В.Н., Петросян Ю.А., Алексеев А.Е. Функциональная интеграция элементов и устройств. Электронная промышленность, 2000, № 4, с.70-88.
Трубочкина Н.К. Схемотехника ЭВМ. М: МИЭМ, 2008.
Слайд 29
О руководителе
научного направления
Трубочкина Надежда Константиновна - доктор
технических наук, профессор, Россия, Москва,
МИЭМ, кафедра вычислительных систем
и сетей.
Работает в области информационных,
компьютерных и интернет-технологий, занимается
теоретическими разработками в области переходной
схемотехники для 3-d СБИС.
Автор более 80 научных работ и изобретений в
области создания элементной базы и программного
обеспечения для проектирования компьютерных систем.
Читает лекции в Московском институте электроники и математики по компьютерной схемотехнике и Web-дизайну. Ведет курс в интернете по Flash-технологиям.
Имеет сайты:
http://nadin.miem.edu.ru
http://distant.miem.edu.ru
http://testing.miem.edu.ru