- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Временные ряды
Содержание
- 2. Три составляющие временного рядаДолговременная тенденция ТПериодические (циклические или сезонные) колебания SСлучайная компонентаЕ
- 3. Модели временного ряда:Основная задача эконометрического исследования временного
- 4. Автокорреляция уровней временного ряда – это корреляционная
- 5. τ – величина сдвига во времени, или
- 6. Свойства коэффициента автокорреляции:характеризует тесноту только линейной связи
- 7. Автокорреляционная функция временного ряда (АКФ) – это
- 8. Моделирование тенденции временного ряда Аналитическое выравнивание – это
- 9. Для определения вида тенденции применяются следующие методы:
- 10. Выбор вида тенденции на основе качественного анализа
- 11. Моделирование периодических колебаний Построение аддитивной и мультипликативной моделей
- 12. 1 этап. Выравнивание исходного ряда методом скользящей средней
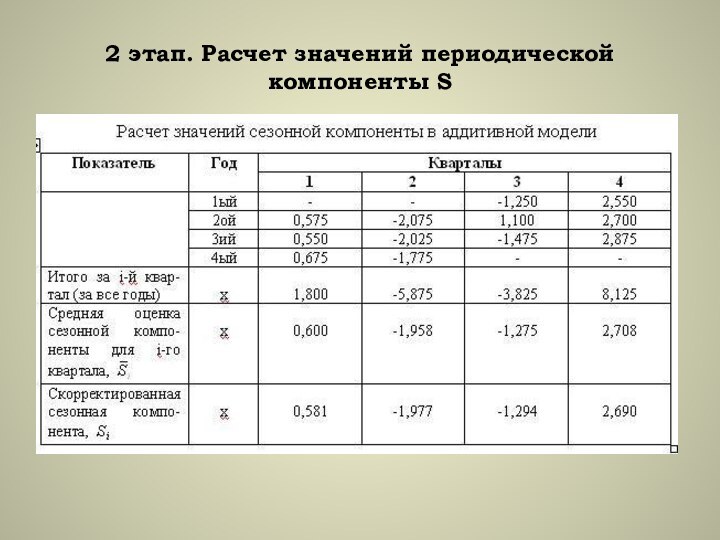
- 13. 2 этап. Расчет значений периодической компоненты S
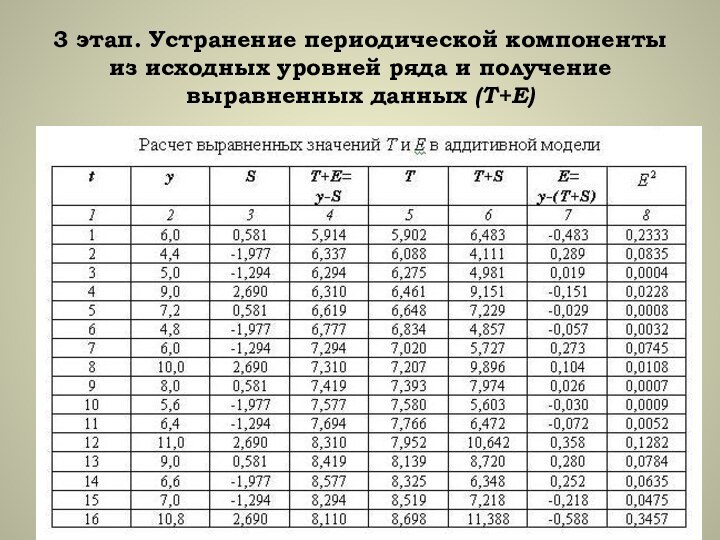
- 14. 3 этап. Устранение периодической компоненты из исходных уровней ряда и получение выравненных данных (Т+Е)
- 15. Скачать презентацию
- 16. Похожие презентации
Три составляющие временного рядаДолговременная тенденция ТПериодические (циклические или сезонные) колебания SСлучайная компонентаЕ








Слайд 2
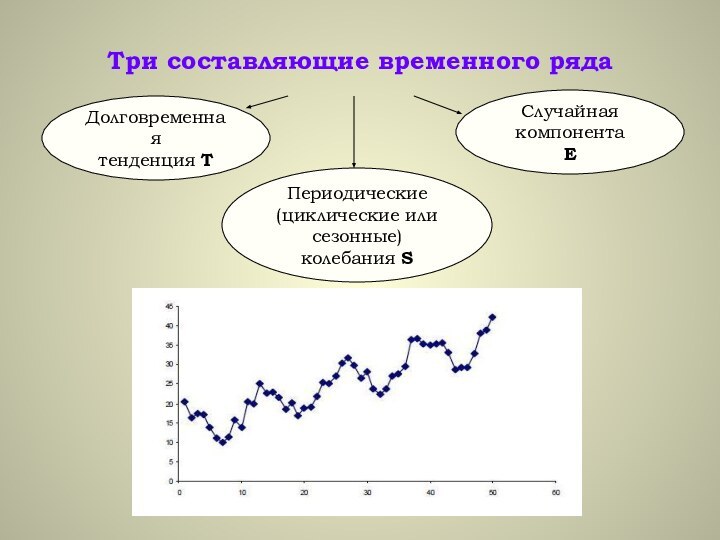
Три составляющие временного ряда
Долговременная
тенденция Т
Периодические
(циклические или
сезонные)
Слайд 3
Модели временного ряда:
Основная задача эконометрического исследования временного ряда:
выявление
и количественное выражение его компонент (тенденции, периодичности, случайной компоненты)
в целях их использования для прогнозирования будущих значений ряда.
1) аддитивная
2) мультипликативная
3) смешанная
Слайд 4
Автокорреляция уровней временного ряда –
это корреляционная зависимость
между последовательными уровнями временного ряда.
Измеряется с помощью линейного
коэффициента корреляции между уровнями исходного временного ряда и уровнями ряда, сдвинутыми на несколько шагов назад во времени:
Слайд 5 τ – величина сдвига во времени, или лаг
Например, лаг τ=1 означает, что ряд сдвинут на один
период (момент) назад и т.д. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.τ=1 =>
τ=2 =>
Слайд 6
Свойства коэффициента автокорреляции:
характеризует тесноту только линейной связи текущего
и предыдущего уровней ряда, поэтому по данному коэффициенту можно
судить о наличии линейной или близкой к линейной тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию, коэффициент автокорреляции может приближаться к нулю;по знаку коэффициента автокорреляции нельзя судить о возрастающей или убывающей тенденции в уровнях ряда.
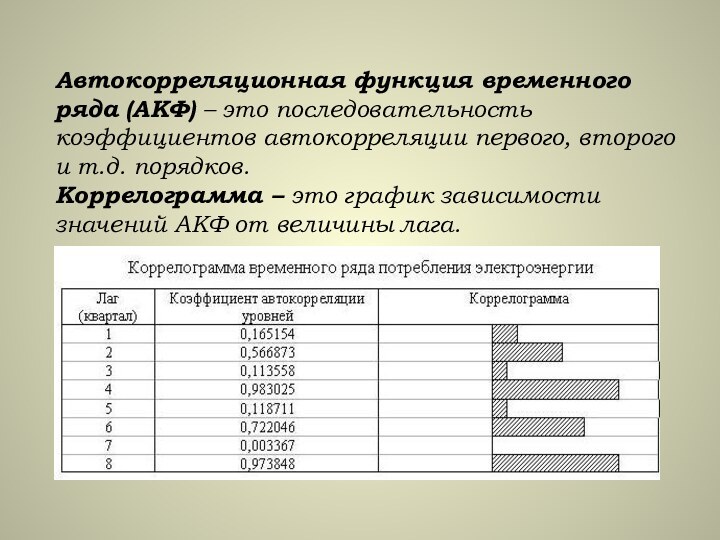
Слайд 7 Автокорреляционная функция временного ряда (АКФ) – это последовательность
коэффициентов автокорреляции первого, второго и т.д. порядков. Коррелограмма –
это график зависимости значений АКФ от величины лага.
Слайд 8
Моделирование тенденции временного ряда
Аналитическое выравнивание – это построение
аналитической функции, характеризующей зависимость уровней ряда от времени, т.е.
построение тренда:линейный тренд
экспоненциальный тренд
гипербола
тренд в форме степенной функции
Слайд 9
Для определения вида тенденции применяются следующие методы:
– качественный
анализ изучаемого процесса;
– построение и визуальный анализ графика зависимости
уровней ряда от времени;– расчет и анализ показателей динамики временного ряда (абсолютные приросты, темпы роста и др.);
– метод перебора, при котором строятся тренды различного вида с последующим выбором наилучшего на основании значения скорректированного коэффициента детерминации.
Слайд 10
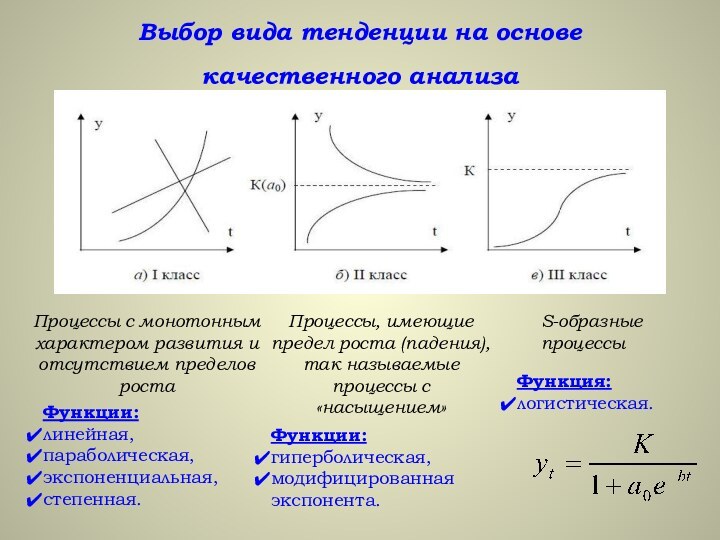
Выбор вида тенденции на основе качественного анализа
Процессы
с монотонным характером развития и отсутствием пределов роста
Функции:
линейная,
параболическая,
экспоненциальная,
степенная.
Процессы, имеющие предел роста (падения), так называемые процессы с «насыщением»
Функции:
гиперболическая,
модифицированная экспонента.
S-образные
процессы
Функция:
логистическая.
Слайд 11
Моделирование периодических колебаний
Построение аддитивной и мультипликативной моделей сводится
к расчету значений T, S, E для каждого уровня
ряда.Процесс построения модели включает в себя следующие этапы:
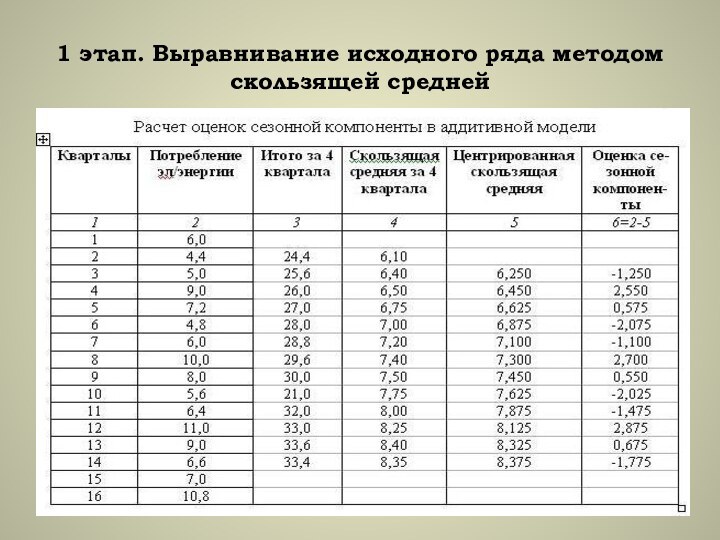
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений периодической компоненты S.
3. Устранение периодической компоненты из исходных уровней ряда и получение выравненных данных (Т+Е) в аддитивной или (Т•Е) в мультипликативной модели.
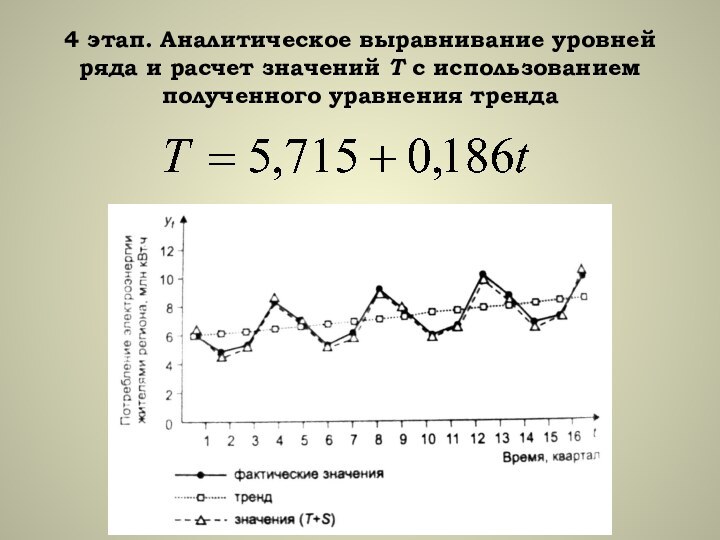
4. Аналитическое выравнивание уровней ряда и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т+S) или (Т•S).
6. Расчет абсолютных и/или относительных ошибок.





























