Слайд 2
Первые учения о формах
и способах рассуждений возникли в странах Древнего Востока (Китай,
Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древнегреческими мыслителями.
Основы формальной логики заложил Аристотель, который впервые отделил логические формы речи от ее содержания. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления
Слайд 3
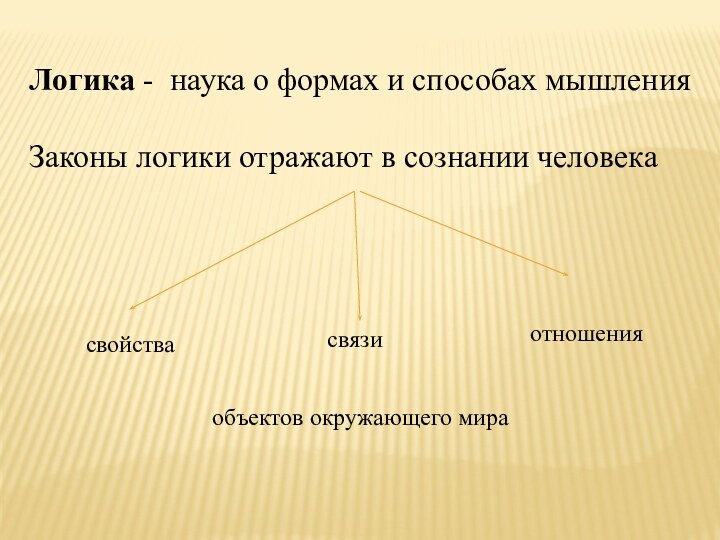
Логика - наука о формах и способах мышления
Законы
логики отражают в сознании человека
свойства
связи
отношения
объектов окружающего мира
Слайд 4
Формы Мышления
Понятие
Высказывание
Умозаключение
Слайд 5
Понятие - это форма мышления, фиксирующая основные, существенные
признаки объекта.
Между множествами (объемами понятий) могут быть различные виды
отношений:
· равнозначность, когда объемы понятий полностью совпадают;
· пересечение, когда объемы понятий частично совпадают;
· подчинения, когда объем одного понятия полностью входит в объем другого и т.д
Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используются диаграммы Эйлера-Венна.
Слайд 6
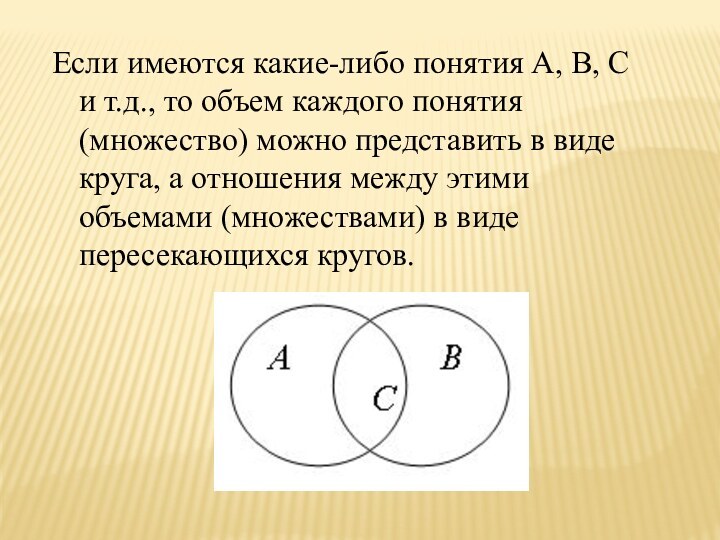
Если имеются какие-либо понятия A, B, C и
т.д., то объем каждого понятия (множество) можно представить в
виде круга, а отношения между этими объемами (множествами) в виде пересекающихся кругов.
Слайд 7
Отобразить с помощью диаграммы Эйлера-Венна соотношение между
объемами понятий натуральные числа и четные числа.
Объем понятия
натуральные числа включает в себя множество целых положительных чисел А
Объем понятия четные числа включает в себя множество отрицательных и положительных четных чисел В.
Эти множества пересекаются, т.к. включают в себя множество положительных четных чисел С.
Слайд 8
- это форма мышления, в которой что-либо утверждается
или отрицается о свойствах реальных предметов и отношениях между
ними.
Высказывание
Слайд 9
Высказывания обозначаются именами логических переменных, которые могут принимать
лишь два значения:
1 - ИСТИНА
0 - ЛОЖЬ
Слайд 10
Истинным будет суждение, в котором связь понятий правильно
отражает свойства и отношения реальных вещей.
Ложным суждение будет
в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности.
Слайд 11
Обоснование истинности или ложности простых высказываний решается вне
алгебры логики.
Например, истинность или ложность высказывания: "Сумма углов
треугольника равна 180 градусов" устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным
Слайд 12
Умозаключение
- это форма мышления, с помощью которой из
одного или нескольких суждений (посылок) может быть получено новое
суждение (заключение).
Слайд 13
Умозаключения бывают:
1. дедуктивные,
2. индуктивные
3. по аналогии.
В дедуктивных умозаключениях рассуждения ведутся от общего к частному.
Например, из двух суждений: «Все металлы электропроводны» и «Ртуть является металлом» путем умозаключения можно сделать вывод, что: «Ртуть электропроводна».
Слайд 14
В индуктивных умозаключениях рассуждения ведутся от частного
к общему.
Например, установив, что отдельные металлы - железо,
медь, цинк, алюминий и т.д. - обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны.
Слайд 15
Умозаключение по аналогии представляет собой движение мысли от
общности одних свойств и отношений у сравниваемых предметов или
процессов к общности других свойств и отношений.
Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле.
Слайд 16
Самостоятельное задание
1. Отобразить с помощью диаграммы Эйлера-Венна соотношения
между следующими объемами понятий:
а) целые и натуральные числа;
б) четные и нечетные числа
Слайд 17
2. Приведите примеры понятий, суждений, умозаключений и доказательств
из различных наук: математики; информатики; физики и химии.
Слайд 18
Основные понятия математической логики
Алгебра логики – это раздел
математики, изучающий высказывания, рассматриваемые со стороны их логических значений
(истинности и ложности) и логических операций над ними
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно
Для обозначения истины (истинного высказывания) используется символ 1 (True), а для обозначения лжи (ложного высказывания) используется символ 0 (False).
True = 1 False = 0
True > False
Слайд 20
Что такое логические выражения?
Логическое выражение – это некоторое
высказывание, по поводу которого можно заключить истинно оно или
ложно.
Логическое выражение , подобно математическому выражению выполняется (вычисляется), но в результате получается не число, а логическое значение (логическая величина)
Слайд 21
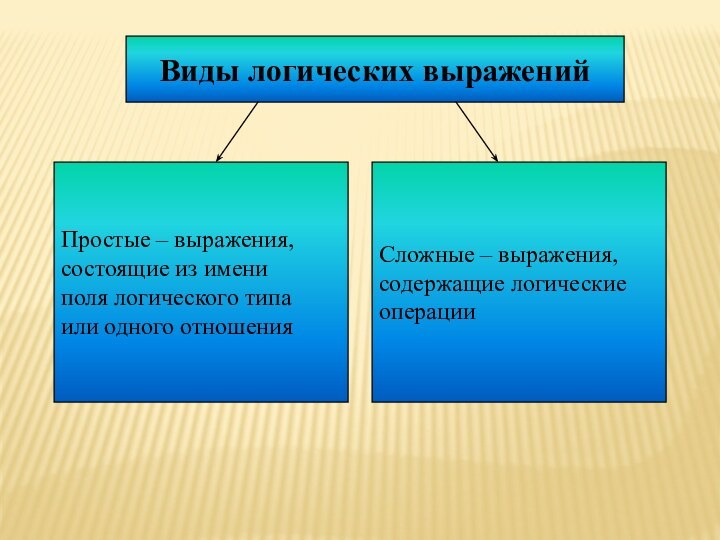
Виды логических выражений
Простые – выражения,
состоящие из имени
поля логического типа
или одного отношения
Сложные – выражения,
содержащие
логические
операции
Слайд 22
Примеры простых высказываний
Шесть первых выражений называются отношениями.
Слайд 23
Осадки = «дождь» 5. Автор = «Толстой Л.Н.»
Давление >
740 6. Фамилия = «Русанов»
Влажность 100 7. Цветоводство
Полка < 5 8.
Танцы
Знаки отношений :
= равно
<> не равно
> больше
< меньше
>= больше или равно
<= меньше или равно
Слайд 24
ОТНОШЕНИЯ
Отношения – это выражения в которых имена полей
базы данных связываются в соответствующие знаки отношений
Слайд 25
Особенности выполнения отношений для символьных величин.
Отношение «равно» истинно
для двух символьных величин, если их длина одинакова и
все соответствующие символы совпадают
Символьные величины можно сопоставлять и в отношениях <, >, <=, >= по принципу: сравниваются между собой не сами символы, а их внутренние коды
Слайд 26
Употребляемые в обычной речи слова и словосочетания «не»,
«и», «или», «если…то», «тогда и только тогда» и др.
позволяют из уже заданных высказываний строить более сложные высказывания. Такие слова и словосочетания называют логическими связками.
Сложные логические выражения
Сложные логические выражения состоят из простых, с помощью логических операций (связок)
Слайд 27
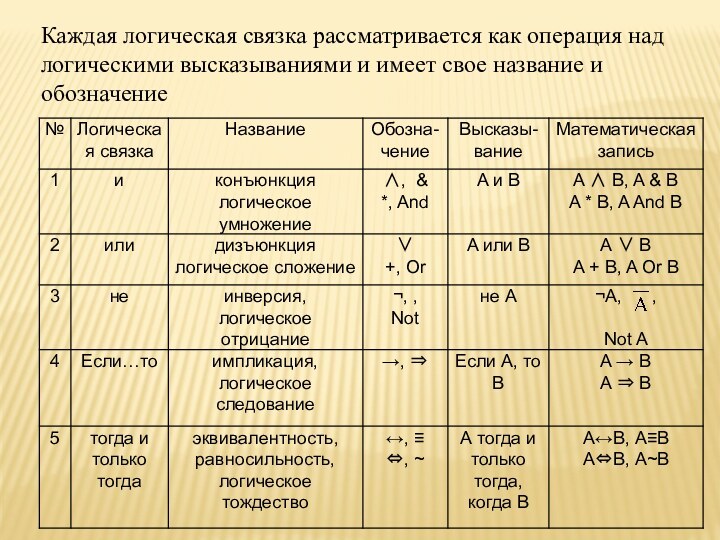
Каждая логическая связка рассматривается как операция над логическими
высказываниями и имеет свое название и обозначение
Слайд 28
Логическое умножение
Обозначение :
в русском языке – и
в английском
языке – and
в математической логике - /\
В результате логического
умножения получается истина, если
оба операнда (логические величины) истинны.
Слайд 29
Логическое сложение
Обозначение :
в русском языке – или
в английском
языке – or
в математической логике - \/
В результате логического
сложение получается истина, если значение хотя бы одного операнда истинно
Слайд 30
Логическое отрицание
Обозначение :
в русском языке – не
в английском
языке – not
в математической логике - x
Отрицание изменяет значение
логического выражения на противоположное.
Отрицание – одноместная операция, она применяется к одному логическому операнду
Слайд 31
Порядок действий
Not (отрицание)
And (логическое умножение)
Or (логическое сложение)
>,=,
Слайд 32
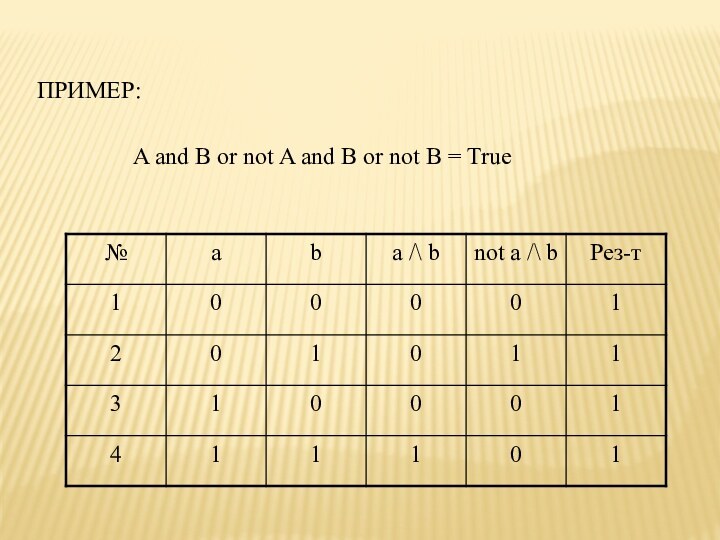
ПРИМЕР:
A and B or not A and B
or not B = True