Слайд 2
Лекция 1
Вводная
Вопросы: 1. Что такое физика и
что она изучает.
2. Основы кинематики
1. Слово «физика» произошло от греческого слова, что означает природа. Оно впервые появилось в сочинениях одного из величайших мыслителей древности – Аристотеля, жившего в IVв. до н.э. В русский язык слово «физика» было введено М.В. Ломоносовым, когда он издал в России первый учебник физии в переводе с немецкого языка.
Физика – одна из основных наук о природе.
По методам исследования физика делиться на теоретическую экспериментальную.
Физика – основа техники. Физика изучает материю.
Материя – это всё то, что существует во Вселенной независимо от нашего (небесные тела, растения, животные и т.д.).
Материя существует в виде двух категорий: в виде вещества в виде поля (электромагнитное, электрическое, биологическое, торсионное, гравитационное т.д.).
Слайд 3
Механика – это часть физики, которая изучает закономерности

механического движения и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка – это тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки – абстрактное, но его ведение облегчает решение практических задач. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.
Под воздействием тел друг на друга тела могут деформироваться, т.е. изменять свою форму и размеры. Поэтому в механике была введена ещё одна модель – абсолютно твёрдое тело.
Абсолютно твёрдое тело – это тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остаётся постоянным.
Слайд 4
Любое движение твёрдого тела можно представить как комбинацию

поступательного и вращательного движений.
Поступательное движение – это движение, при
котором любая прямая, жёстко связанная с движущимся телом, остаётся параллельной своему первоначальному положению.
Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
2. Кинематика – изучает движение тел, не рассматривая причины,
которые это движение обуславливают.
Для характеристики движения материальной точки вводиться векторная величина – скорость, которая определяется как быстрота движения, так и его направление в данный момент времени.
Простейшим видом механического движения абсолютно твердого тела является поступательное движение - такое движение, при котором тело перемещается параллельно самому себе. При этом все точки описывают конгруэнтные (одинаковые) траекторий, смещенные друг относительно друга.
Поступательное движение абсолютно твердого тела может быть охарактеризовано движением какой-либо одной его точки, например, центра масс.
Для характеристики поступательного движения тела (материальной точка) вводится понятие перемещения.
Перемещением называется вектор, соединяющий начальное положение тела с его конечным положением.
Слайд 5
Мгновенная линейная скорость - физическая величина» равная пределу,
к которому стремится отношение элементарного перемещения S за промежутку
времени t в течение которого совершается это перемещение, при t = 0.
Мгновенная скорость - векторная величина, имеющая тоже направление, что и касательная к траектории, т.к. вектор мгновенной скорости v совпадает с вектором достаточно малого перемещения dS за достаточно малое время dt. Мгновенная скорость численно равна первой производной от перемещения по времени.
Средняя скорость за промежуток времени t = t2 - t1 – это физическая величина, равная отношению вектора перемещения z к длительности промежутка времени t.
Слайд 6
Лекция 2 Законы Ньютона.
Законы сохранения импульса и

механической энергии.
Вопрос: 1. Законы Ньютона.
2. Законы сохранения импульса и механической энергии.
1. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Инертность – это стремление тела сохранять состояние покоя или равномерного прямолинейного движения.
Поэтому первый закон Ньютона называют так же законом инерции.
Механическое движение относительно, и его характер зависит от системы отсчёта. Первый закон Ньютона выполняется не во всякой системе отсчёта, а те системы по отношению к которым он выполняется, называются инерциальными системами отсчёта. Инерциальной системой отсчёта является такая система отсчёта, относительно которой материальная очка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчёта.
Слайд 7
Масса тела – это физическая величина, являющаяся одной
из основных характеристик материи, определяющая её инерционные (инертная масса)
и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10-12 их значения).
Второй закон Ньютона составляет основу не только классической механики, но и всей классической физики. Несмотря на простоту его математической формулировки F=ma
при объяснении его "физического смысла" возникают вполне определенные методические трудности. До сих пор в различные учебных курсах используются различные подходы к "физической" формулировке этого важнейшего закона, причем каждый из них обладает как определенными преимуществами, так и недостатками.
инертная масса тела может быть определена как коэффициент пропорциональности между силой и ускорением, остающийся постоянным для данного тела в соответствии со вторым законом:
Слайд 8
Из формулировки второго закона Ньютона (2) и определения
массы (3) следует, что ускорение тела пропорционально равнодействующей приложенных
к нему сил и обратно пропорционально его инертной массе:
более удобной является импульсная формулировка второго закона Ньютона:
Слайд 9
Согласно третьему закону Ньютона при взаимодействии тел возникают
силы, приложенные к каждому из партнеров. При этом силы
всегда оказываются равными друг другу по величине и противоположно направленными. F2 = – F1
Из законов Ньютона следует, что в случае взаимодействия двух тел, не взаимодействующих с другими, каждое из них должно двигаться с ускорением. Если масса одного из взаимодействующих тел существенно превосходит массу другого, то его ускорение оказывается малым.
Слайд 10
2. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. Из законов Ньютона можно

показать, что при движении в пустом пространстве импульс сохраняется
во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Однако, этот закон сохранения верен и в случаях, когда Ньютоновская механика неприменима (релятивистская физика, квантовая механика). Как отмечалось, он может быть получен как следствие интуитивно-верного утверждения о том, что свойства нашего мира не изменятся, если все его объекты (или начало отсчета!) переместить на некоторый вектор L. В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА. Если понятие импульса в классической механике характеризует поступательное движение тел, момент импульса вводится для характеристики вращения и является следствием утверждения о том, что свойства окружающего мира не изменяются при поворотах (или повороте системы отсчета) в пространстве.
Слайд 11
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ Первоначально в механике были введены

кинетическая энергия (обусловленная движением тела) и потенциальная (обусловленная взаимодействиями
между телами и зависящая от их расположения в пространстве). Конкретное математическое выражение для потенциальной энергии определяется взаимодействиями между объектами. В большинстве механических систем механическая энергия (сумма кинетической и потенциальной) сохраняется во времени (например в случае мяча, упруго ударяющегося о пол). Однако нередки и такие системы, в которых механическая энергия изменяется (чаще всего убывает). Для описания этого были введены диссипативные силы (например, силы вязкого и сухого трения и др.). Со временем выяснилось, что диссипативные силы описывают не исчезновение или возникновение механической энергии, а переходы ее в другие формы (тепловую, электромагнитную, энергию связи и т.д.)
Закон сохранения энергии имеет большое практическое значение, поскольку существенно ограничивает число возможных каналов эволюции системы без ее детального анализа. Так на основании этого закона оказывается возможным априорно отвергнуть любой весьма проект весьма экономически привлекательного вечного двигателя первого рода (устройства, способного совершать работу, превосходящую необходимые для его функционирования затраты энергии).
Слайд 12
Лекция 3
Динамика вращательного движения и механика твердого тела.
Вопросы: 1. Динамика вращательного движения
2. Механика твердого тела
1. Динамика изучает законы движения тел и причины, которые
вызывают или изменяют это движение.
- импульс (количество движения) материальной точки (частицы), m – масса частицы, - скорость частицы.
Масса – мера инертности тела.
Закон сохранения импульса: в замкнутой системе суммарный импульс – величина постоянная. - закон сохранения импульса для замкнутой системы, где n – число частиц (или тел), входящих в систему.
Слайд 13
2. Развитие механики как науки начинается с IIIв.

До н.э., когда древнегреческий учёный Архимед (287-212 до н.э.)
сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г.Галилеем (1564-1642) и окончательно сформулированы английским учёным И.Ньютоном (1643-1727).
Механика Галилея-Ньютона называется классической механикой. В ней изучаются законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света с в вакууме.
Механика делится на три раздела: 1) кинематику 2)динамику 3)статику
ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ - общий закон природы: энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной (сохраняется). Энергия может только превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение (уменьшение) ее энергии равно убыли (возрастанию) энергии взаимодействующих с ней тел и физических полей.
Слайд 14
ЗАКОН АРХИМЕДА - закон гидро- и аэростатики: на

тело, погруженное в жидкость или газ, действует выталкивающая сила,
направленная вертикально вверх, числено равная весу жидкости или газа, вытесненного телом, и приложенная в центре тяжести погруженной части тела. FA= gV, где r - плотность жидкости или газа, V - объем погруженной части тела. Иначе можно сформулировать так: тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость (или газ). Тогда P= mg - FA Открыт др. гр. ученым Архимедом в 212г. до н.э. Является основой теории плавания тел.
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ, механический принцип относительности - принцип классической механики: в любых инерциальных системах отсчета все механические явления протекают одинаково при одних и тех же условиях. Ср. относительности принцип.
ЗАКОН ГУКА - закон, согласно которому упругие деформации прямо пропорциональны вызывающим их внешним воздействиям.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА - закон механики: импульс любой замкнутой системы при всех процессах, происходящих в системе, остается постоянным (сохраняется) и может только перераспределяться между частями системы в результате их взаимодействия.
Слайд 15
Лекция 4 Закон всемирного тяготения,
законы Кеплера. Основы молекулярной
физики.
Вопросы: 1. Закон всемирного тяготения
2. Законы Кеплера
3. Основы молекулярной физики.
1. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ - закон тяготения Ньютона: все тела притягиваются друг к другу с силой прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними: , где M и m - массы взаимодействующих тел, R - расстояние между этими телами, G - гравитационная постоянная (в СИ G=6,67.10-11 Н.м2/кг2.
Исаак Ньютон (1642- 1726) английский математик и философ, открывший закон всемирного тяготения
Слайд 16
2. К началу XVII столетия большинство учёных убедилось

в справедливости гелиоцентрической системы мира. И.Кеплер (1571-1630), обработав и
уточнив результаты многочисленных наблюдений датского астронома Т.Браге (1546-1601), изложил законы движения планет.
Каждая планета движется по эллипсу, в одном из фокусов которого находиться Солнце
Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.
Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
3. Молекулярная физика и термодинамика изучают свойства и поведение макроскопических систем, т.е. систем, состоящих из огромного числа атомов и молекул. Типичные системы, с которыми мы сталкиваемся в повседневной жизни, содержат около 1025 атомов.
Основное уравнение молекулярно-кинетической теории идеального
газа. Эта теория создана немецким физиком Р. Клаузисом в 1957
году для модели реального газа, которая называется идеальный газ.
Основные признаки модели:
расстояния между молекулами велики по сравнению с их размерами;
взаимодействие между молекулами на расстоянии отсутствует;
при столкновениях молекул действуют большие силы отталкивания;
время столкновения много меньше времени свободного движения между столкновениями.
Слайд 17
Давление идеального газа пропорционально произведению концентрации молекул на
среднюю кинетическую энергию поступательного движения молекулы. Это утверждение можно
считать другой формулировкой основного уравнения молекулярно-кинетической теории идеального газа.
Из основного уравнения молекулярно-кинетической теории можно получить формулу для расчета средней квадратичной скорости молекул.
Уравнение Менделеева-Клапейрона:
Слайд 18
Лекция 5
Вопросы: 1. Основы кинетической теории.
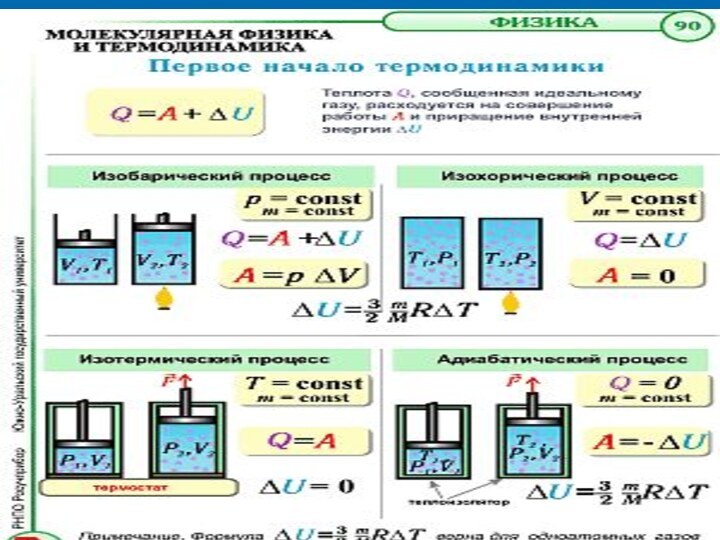
2. Первое начало термодинамики.
1. КИНЕТИКА (от греческого kinetikos - приводящий в движение), раздел механики, объединяющий статику и динамику.
Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики.
Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении.
Слайд 19
Идея об атомном строении вещества высказана древнегреческим философом

Демокритом (460—370 до н. э.). Атомистика возрождается вновь лишь
в XVII в. и развивается в работах М. В. Ломоносова, взгляды которого на строение вещества и тепловые явления были близки к современным. Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Максвелла и Л. Больцмана.
Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.
Слайд 20
2. Рассмотрим термодинамическую систему, для которой механическая энергия

не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя
энергия системы может изменяться в результате различных процессов, например совершения над системой рабооты или сообщения ей теплоты. Так, вдвигая поршень в цилиндр, в котором находится газ, мы сжимаем этот газ, в результате чего его температура повышается, т.е. тем самым изменяется (увеличивается) внутренняя энергия газа. С другой стороны, температуру газа и его внутреннюю энергию можно увеличить за счет сообщения ему некоторого количества теплоты — энергии, переданной системе внешними телами путём теплообмена (процесс обмена внутренними энергиями при контакте тел с разными температурами).
Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия механического движения может превращаться в энергию теплового движения, и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.
Допустим, что некоторая система (газ, заключенный в цилиндр под поршнем),
обладая внутренней энергией U1, получила некоторое количество теплоты Q и, перейдя в новое состояние, характеризующееся внутренней энергией U2, совершила работу.
Слайд 21
А над внешней средой, т. е. против внешних

сил. Количество теплоты считается положительным, когда оно подводится к
системе, а работа — положительной, когда система совершает ее против внешних сил. Опыт показывает, что в соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во второе изменение внутренней энергии U=U2 – U1 будет одинаковым и равным разности между количеством теплоты Q, полученным системой, и работой А, совершенной системой против внешних сил:
U=Q – A или Q=U+A (1.1)
Уравнение (1.1) выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. Выражение (1.1) в дифференциальной форме будет иметь вид: dQ=dU+dA или в более корректной форме бQ=dU+бА (1.2)
где dU — бесконечно малое изменение внутренней энергии системы, бА — элементарная работа, бQ — бесконечно малое количество теплоты. В этом выражении dU является полным дифференциалом, а бА и бQ таковыми не являются. В дальнейшем будем использовать запись первого начала термодинамики в форме (1.2).
Слайд 22
Из формулы (1.1) следует, что в СИ количество
теплоты выражается в тех же единицах, что работа и
энергия, т. е. в джоулях (Дж).
Если система периодически возвращается в первоначальное состояние, то изменение её внутренней энергии U=0. Тогда, согласно первому началу термодинамики, A=Q , т.е. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, — невозможен (одна из формулировок первого начала термодинамики).
Слайд 24
Лекция 6
Вопросы: 1. Энтропия
2. Второе начало термодинамики
3. Третье начало термодинамики
4. Свойство реальных газов
5. Свойства жидкостей
6.Свойства твёрдых тел
1. Второе начало термодинамики является наиболее фундаментальной аксиомой в современной картине природы, определяющей свойства понятия - энтропия. Однако парадоксальным образом из существующих более двух десятков его формулировок ни одна не удовлетворяет обязательным для аксиом условиям полноты - эти формулировки описывают разные свойства энтропии как физической переменной. В существующей аксиоматике не учтено, что энтропия одновременно есть мера информации как физической переменной и её выражения в механике в виде действия.
Слайд 25
Аксиоматически существование действия-энтропии-информации, главные свойства этой переменной и

выбор нуля отсчета для нее (суммарный эквивалент множественных формулировок
второго начала термодинамики) нужно формулировать в следующем виде:
I. Существует иерархическая функция состояния системы - действие-энтропия-информация, определённая в фазовом пространстве, которую можно выразить в двух равноправных формах
S = K(k) lnQ(k) или S = -K(k) lnW(k)
- мера количества информации (мера фазового пространства) в пределах заданных признаков и условий для наиболее вероятного состояния системы из многих элементов (для уровня иерархии k число возможных состояний системы есть Q(k) или вероятности состояний системы - W(k) , а множитель K(k) - адиабатический инвариант данного иерархического уровня системы - единица измерения энтропии-информации с размерностью действия). Физическая система, не содержащая информации о себе самой, не может реализоваться.
II. Действие-энтропия-информация есть характеристика максимума вероятности состояния системы, которая нормирована по отношению к энергии и к числу элементов системы, что определяет её как мнимую составляющую действия-энтропии-информации в виде функции комплексного переменного.
Слайд 26
Действие-энтропию-информацию порождает процесс синтеза информации - запоминание случайного

выбора, в котором критерии запоминания (устойчивости) зависят от экстремумов
действия-энтропии-информации и её производства. В общем виде они заданы в комплексной плоскости. Вечное равновесие невозможно. Случай синтеза информации на основе принципа максимума производства действия-энтропии-информации (максимума способности к превращениям) определяет условия разрушения равновесия и перехода к следующей ступени иерархии роста действия-энтропии-информации. Направление самопроизвольных процессов задают экстремумы действия-энтропии-информации как функции комплексного переменного.
III. Действие-энтропия-информация может суммироваться при разных входящих в её определение признаках и условиях, учитывая уравнения связи их между собой. Для любых, входящих в определение действия-энтропии-информации признаков и условий, существует свой нуль отсчёта, который зависит от них. Действие-энтропия-информация есть положительно определённая переменная, однако существование разных нулей отсчета разрешает в конкретных задачах использовать ее с отрицательным знаком. (А. Хазен).
Слайд 27
2. Первое начало термодинамики, выражая закон сохранения и

превращения энергии, не позволяет установить направление протекания термодинамических процессов.
Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются.
Появление второго начала термодинамики связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики определяет направление протекания термодинамических процессов.
Используя понятие энтропии и неравенство Клаузиуса , второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идёт о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной).
Слайд 28
Кроме того, отметим ещё раз, что энтропия остаётся

постоянной в замкнутой системе только при обратимых процессах. При
необратимых процессах в замкнутой системе энтропия всегда возрастает.
Формула Больцмана (S=kln W) позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему.
Укажем еще две формулировки второго начала термодинамики:
1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Можно довольно просто доказать эквивалентность формулировок Кельвина и Клаузиуса. Кроме того, показано, что если в замкнутой системе провести воображаемый процесс, противоречащий второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это
же доказывает эквивалентность формулировки Клаузиуса (а следовательно, и Кельвина) и статистической формулировки, согласно которой энтропия замкнутой системы может убывать.
Слайд 29
3. Открытие третьего начала термодинамики связано с нахождением

химического средства - величины , характеризующих способность различных веществ
химически реагировать друг с другом . Эта величина определяется работой W химических сил при реакции . Первое и второе начало термодинамики позволяют вычислить химическое средство W только с точностью до некоторой неопределенной функции . Чтобы определить эту функцию нужны в дополнении к обоим началам термодинамики новые опытные данные о свойствах тел . Поэтому
Нернстоном были предприняты широкие экспериментальные исследования поведение веществ при низкой температуре .
В результате этих исследований и было сформулировано третье начало термодинамики : по мере приближения температуры к 0 К энтропия всякой равновесной системы при изотермических процессах перестает зависить от каких-либо термодинамических параметров состояния и в пределе ( Т= 0 К) принимает одну и туже для всех систем универсальную постоянную величину , которую можно принять равной нулю .
Общность этого утверждения состоит в том , что , во-первых , оно относится к любой равновесной системе и , во-вторых , что при Т стремящемуся к 0 К энтропия не зависит от значения любого параметра системы. Таким образом по третьему началу,
lin [ S (T,X2) - S (T,X1) ] = 0 (1.12) или lim [ dS/dX ]T = 0 при Т ( 0 (1.13)
Слайд 30
где Х - любой термодинамический параметр (аi или
Аi).
Предельно значение энтропии , поскольку оно одно и тоже
для всех систем
, не имеет никакого физического смысла и поэтому полагается равным нулю
(постулат Планка). Как показывает статическое рассмотрение этого вопроса , энтропия по своему существу определена с точностью до некоторой постоянной
(подобно, например, электростатическому потенциалу системы зарядов в какой либо точке поля). Таким образом , нет смысла вводить некую «абсолютную энтропию», как это делал Планк и некоторые другие ученые.
Слайд 31
4. Поведение реального газа можно описать с высокой
точностью с помощью вириального уравнения (или уравнения с вириальными
коэффициентами). Идея состоит в отказе от минимального числа параметров и использовании бесконечных рядов - разложений
по степеням 1/V:
Коэффициенты B2, B3, ... (которые зависят от температуры и природы рассматриваемого газа, но не зависят от плотности и давления) называются соответственно вторым, третьим, ... вириальными коэффициентами. Первый вириальный коэффициент равен 1. Второй вириальный коэффициент обычно более важен, чем последующие, поскольку для большинства случаев B2 /Vm >> B3 /V2m >> ... .
Уравнение состояния в виде бесконечного ряда (1.15) было предложено Тиссеном в 1885 г. Однако основное развитие вириальное уравнение получило в 1901 г. в работе Камерлинг-Оннеса, который рассмотрел несколько вариантов этого уравнения и предложил называть его коэффициенты вириальными.
Слайд 32
Если подходить в вириальному уравнению только как к

эмпирическому уравнению состояния, то оно имеет ряд недостатков. Например,
как показывают экспериментальные данные, сходимость ряда не очень хорошая, особенно в области высокой плотности. Кроме того, при высоких плотностях для удовлетворительного описания экспериментальных данных необходимо использовать большое число членов ряда, а для этого нужно экспериментально определять большое число вириальных коэффициентов. Более того, часто тот же набор экспериментальных данных можно более точно описать с помощью других эмпирических уравнений с меньшим числом параметров. Однако исключительная важность вириального уравнения состояния заключается в том, что это единственное из известных уравнений состояния, имеющее строгую теоретическую основу. Как будет показано в главе 2, каждый вириальный коэффициент можно выразить через силы межмолекулярного взаимодействия. Так, второй вириальный коэффициент отражает парные взаимодействия, третий – тройные и т.д. Таким образом, вириальное уравнение состояния позволяет объяснить свойства газа с позиции межмолекулярных взаимодействий.
Для некоторых целей вириальное уравнение удобнее записать в виде разложения по степеням p:
pVm = RT (1 + B2'p + B3'p2 + ...) (1.16)
Таким образом, вириальное уравнение является примером того, когда простое выражение (в данном случае pVm = RT) представляет собой только первый член ряда разложения по степеням переменной (в данном случае p или Vm).
Слайд 33
5. Молекулы в жидкостях находятся близко друг
к другу, примерно на расстояниях равных размерам самих молекул.
Это является причиной высокого молекулярного ван-дер-ваальсового давления, которое равно
Для воды, например, он равен около 11000 атм. Удельный объем жидкостей в тысячи раз меньше чем газов, следовательно, отношение
в жидкостях в миллионы раз больше, чем в газах. Поэтому можно пренебречь внешним давлением, и уравнение Ван-дер-Ваальса примет вид
Большой величиной молекулярного давления объясняется ничтожно малая сжимаемость жидкостей. Это сразу видно из уравнения кривой Ван-дер-Ваальса.
Слайд 34
Коэффициент сжимаемости c жидкости – относительное изменение объема
dV при изменении давления на единицу т.е.
Опыт показывает,
что коэффициент сжимаемости большинства жидкостей лежит в пределах от 10-4 до 10-5
.
Коэффициент сжимаемости жидкости зависит от давления. Он возрастает с повышением температуры. К этому результату можно прийти и опытным путем и исходя из уравнения Ван-дер-Ваальса. Поскольку это уравнение связывает температуру, объем и давление, то из него можно вычислить величину
Слайд 35
При расчете необходимо учитывать, что постоянные a и
b на самом деле зависят от температуры. Совокупность опытных
данных позволила получить эмпирическую формулу для коэффициента сжимаемости жидкости:
где A – некоторая функция, возрастающая с температурой, p – внешнее давление и pT – давление, связанное с силами Ван-дер-Ваальса (a/V2) при температуре T. Эта формула показывает, что коэффициент сжимаемости растет с повышением температуры и уменьшается с ростом давления.
Слайд 38
Лекция7
Вопросы: 1. Электростатика.
2. Потенциал электрического поля.
3. Проводники в электрическом поле.
1. В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между такими зарядами, было отмечено еще во времена Гомера. Слово «электричество» происходит от греческого elektron (янтарь), поскольку первые описанные в истории наблюдения электризации трением связаны именно с этим материалом. В 1733 Ш.Дюфе (1698–1739) открыл, что существуют электрические заряды двух типов. Заряды одного типа образуются на сургуче, если его натирать шерстяной тканью, заряды другого типа – на стекле, если его натирать шелком. Одинаковые заряды отталкиваются, разные – притягиваются. Заряды разных типов, соединяясь, нейтрализуют друг друга.
Слайд 39
2. Вблизи электрических зарядов существует электрическое поле, величина

которого в данной точке пространства равна, по определению, отношению
силы, действующей на точечный пробный заряд, помещенный в эту точку, к величине пробного заряда, опять-таки при условии, что пробный заряд достаточно мал и не изменяет распределения зарядов, создающих поле. Согласно этому определению, действующая на заряд q сила F и напряженность электрического поля E связаны соотношением: F = qE. Потенциал поля точечного заряда Q в однородной изотропной среде
с диэлектрической проницаемостью :
3. Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут вращаться. Перемещение зарядов (ток) продолжается до
тех пор, пока не установиться равновесие распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю,
Слайд 40
то в проводнике возникло бы упорядоченное движение зарядов

без затраты энергии от внешнего источника, что противоречит закону
сохранения энергии. Итак, напряжённость поля во всех точках внутри проводника равна нулю: E=0.
Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные – по полю, отрицательные – против поля. На одном конце проводника будут скапливаться избыток положительного заряда, на другом – избыток отрицательного. Эти заряда называются индуцированными. Процесс будет проходить до тех пор, пока напряжённость поля внутри проводника не станет равной нулю, а линии напряжённости вне проводника – перпендикулярными его поверхности. Таким образом, нейтральный проводник, внесённый в электростатическое поле, разрывает часть линии напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией.
Слайд 41
Лекция 8
Вопросы: 1. Постоянный электрический ток.
2. Работа и мощность
тока
1. Постоянный электрический ток – направленное движение заряженных частиц.
Условия существования электрического тока:
1. Наличие заряженных частиц ( электроны в металлах, положительные и отрицательные заряженные ионы в электролитах и газах, дырки и электроны в полупроводниках).
2. Наличие электрического поля (наличие силы, действующей со стороны поля на эти заряженные частицы).
За направление тока принимается направление, обратное движению электронов: Fk = Eq0=-Ee
Слайд 42
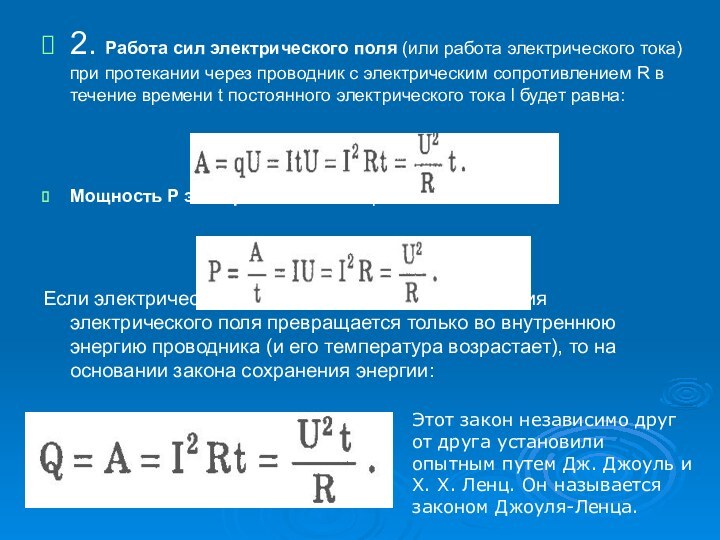
2. Работа сил электрического поля (или работа электрического
тока) при протекании через проводник с электрическим сопротивлением R
в течение времени t постоянного электрического тока l будет равна:
Мощность Р электрического тока равна:
Если электрический ток протекает в цепи, где энергия электрического поля превращается только во внутреннюю энергию проводника (и его температура возрастает), то на основании закона сохранения энергии:
Этот закон независимо друг от друга установили опытным путем Дж. Джоуль и X. X. Ленц. Он называется законом Джоуля-Ленца.
Слайд 43
Лекция 9
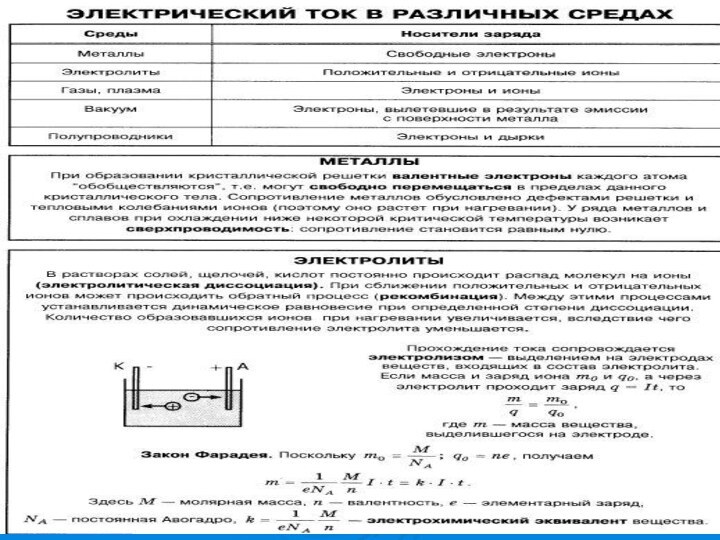
Вопросы: 1. Электрический ток в различных средах
2. Магнитное
поле и его свойства
3. Закон Био-Савара-Лапласа
1. Хорошими проводниками, т.е веществами с большим количеством свободных заряженных частиц, являются водные растворы или расплавы электролитов и ионизованный газ – плазма.
В вакуумных электронных приборах электрический ток образуют потоки электронов.
Коэффициент пропорциональности называют температурным коэффициентом сопротивления. Он характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивлению проводника при нагревании на 1 К.
У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается.
Слайд 44
Многие металлы при температуре ниже 25 К полностью
теряют сопротивление – становятся сверхпроводниками. Выделения теплоты в сверхпроводящей
обмотке не происходит.
Очень сильное магнитное поле разрушает сверхпроводящее состояние.
При нагревании кремния кинетическая энергия валентных электронов повышается, и наступает разрыв валентных связей.
Проводимость полупроводников, обусловленную наличием у них свободных электронов, называют электронной проводимостью.
При нагревании от 300 до 700 К число свободных носителей заряда увеличивается от 1017 до 1024 1/м3. Это приводит к уменьшению сопротивления.
Примеси, легко отдающие электроны и, следовательно, увеличивающее число свободных электронов, называют донорными примесями (образуют проводник n-типа)
Акцепторные примеси создают дырки: образуется проводник р-типа.
Свойства p-n перехода используются в полупроводниках для усиления и генерации электрических колебаний.
Слайд 45
Термоэлектронная эмиссия – свойство тел, нагретых до высокой

температуры, испускать электроны.
На движение электронов наряду с полем, созданным
зарядами на электродах, существенное влияние оказывает поле пространственного заряда электронного облака у катода.
Электронный пучок, попадая на тела, вызывает их нагревание.
При торможении быстрых электронов, попадающих на вещество, возникает рентгеновское излучение.
Электронные пучки отклоняются электрическим полем.
Также электронный пучок отклоняется в магнитной среде.
При растворении электролитов под влиянием электрического поля полярных молекул воды происходит распад молекул электролитов на ионы. Этот процесс называется электрической диссоциацией.
Степень диссоциации, т.е доля молекул в растворенном веществе, распавшихся на ионы, зависит от температуры, концентрации раствора и диэлектрической проницаемости растворителя.
Перенос заряда в водных растворах или расплавах электролитов осуществляется ионами, такую проводимость называют ионной.
Процесс выделения на электроде вещества, связанный с окислительно-восстановительными реакциями, называют электролизом.
При помощи электролиза осуществляют очистку металлов от примесей.
Слайд 47
2. Опыт показывает, что, подобно тому, как в

пространстве, окружающем электрические заряды, возникает электростатическое поле, так и
в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).
Электрическое поле действует как на неподвижные, так и на движущиеся в нём электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.
Слайд 48
Опыты показывают, что магнитное поле оказывает на рамку

с током ориентирующее действие, поворачивая её определённым образом. Этот
результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к раме. За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующие на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.
Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля.
Так как магнитное поле является силовым, то его, по аналогии с электрическим, выражают с помощью линии магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.
Слайд 49
До сих пор мы рассматривали макроскопические токи, текущие
в проводниках. Однако, согласно предположению французского физика А. Ампера
(1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми мокро- и микротоками, т. е. при одном в том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.
Слайд 50
3. Закон Био-Саваpа-Лапласа в теоpии магнитного поля отвечает
на аналогичный вопpос, что и закон Кулона в теоpии
электpостатического поля. Каково магнитное поле точечного заpяда? В отличие от электpического поля магнитное поле не только воздействует лишь на движущиеся заpяды, но и создается лишь движущимися заpядами. Обычно движущиеся заpяды пpедставлены токами. Поэтому и pассмотpим постоянный ток, идущий по очень тонкому пpоводу. Пpовод наполнен движущимся со скоpостью v заpядом. Выбеpем малый участок пpовода dl и заpяд, его заполняющий, обозначим чеpез dq. Нас будет интеpесовать магнитное поле от заpяда dq в пpоизвольной точке пpостpанства М. Вспомним закон Кулона.
Слайд 51
Напpяженность электpического поля, создаваемого заpядом dq, обpатно пpопоp-циональна
квадpату pасстояния от заpяда до данной точки поля: dE
~ dq/r2. Закон Био-Саваpа-Лапласа фоpмулиpуется аналогичным обpазом.
Индукция магнитного поля пpямо пpопоpциональна заpяду и обpатно пpопоpциональна квадpату pасстояния от заpяда. Однако магнитное поле еще зависит и от скоpости движения заpяда: индукция магнитного поля пpопоpциональна скоpости движения заpяда и синусу угла между напpавлениями скоpости и pадиуса-вектоpа, пpоведенного от заpяда в данную точку поля. В виде фоpмулы закон Био-Саваpа-Лапласа записывается следующим обpазом:
m0/4p коэффициент в СИ, численно pавный 10-7 гн/м.
Слайд 52
Лекция 10
Вопросы: 1. Электромагнитная индукция
2. Магнитные поля в веществе
3. Электромагнитные колебания
1. «Если какой-нибудь заряд переместился из одной точки в другую, то, очевидно, силы, действующие со стороны этого заряда на другие заряды, изменятся. При непрерывном движении заряда эти силы также должны меняться непрерывно; однако, если распространение действия заряда совершается с конечной скоростью, это изменение будет отставать от перемещения заряда, что приводит к значительным усложнениям теории действия электрических сил. Чтобы учесть специфические эффекты, возникающие при наличии движущихся зарядов, вводится дополнительная характеристика, которую мы и назвали индукцией магнитного поля. Введение этой характеристики позволяет существенно упростить всю теорию электрических явлений
Слайд 53
и не задумываться о том, что электрическое воздействие

распространяется в пространстве с конечной скоростью. Так как приходится
пользоваться двумя понятиями: напряженностью электрического поля и индукцией магнитного поля, - то явления, которые мы будем в дальнейшем изучать, получили общее название электромагнитные явления. Таким образом, известные еще из школьного курса магнитные силы представляют не что иное, как проявление электрических действий, вызванных движущимися зарядами. В природе не существует никаких особых магнитных зарядов, а есть только электрические заряды двух типов, условно называемые положительными и отрицательными. В заключение заметим, что в выражении для силы Лоренца не случайно стоит коэффициент с. Его значение соответствует скорости света в вакууме, а это как раз та самая максимальная скорость, с которой может распространяться электрическое поле заряда, возникшего в данной точке пространства.»
Т.е. в выражении для силы Лоренца (система СГС) коэффициент с - это скорость распространения изменений (смещений) электрического поля, которые в виде токов смещения сопровождают движение зарядов. Из выражения видно, что если бы изменения поля распространялись мгновенно, то никакой силы Лоренца (релятивистского эффекта) не возникало бы.
«... возникновение магнитного поля является чисто релятивистским эффектом, следствием наличия в природе предельной скорости с, равной скорости света в вакууме. Если бы эта скорость была бесконечной (соответственно и скорость распространения взаимодействий), никакого магнетизма вообще не существовало бы.»
Слайд 54
2. Доказанная теорема о циркуляции относится к любому
случаю магнитного поля пpи условии, если оно создано постоянными
токами. Она выполняется и при наличии магнетика, в котором в пpисутствиии внешнего поля возникают связанные токи. В этом случае в правую часть уравнения для циркуляции вектора В должны войти как свободные, так и связанные токи. Рассмотрим такой случай.
Пусть пpоводник с током помещен в магнетик (pис. 3.30). Магнетик может быть неодноpодным и иметь гpаницы (мы pассматpиваем общий случай). Какова циpкуляция вектоpа индукции магнитного поля по контуpу L? Она пpопоpциональна сумме токов, сцепленных с контуpом. Кpоме тока J нужно учесть связанные токи молекул магнетика. Молекулы мы уподобляем магнитным диполям. Только часть диполей-молекул нанизаны на контуp.
Эти диполи как бы обpазуют некую
тpубку, по повеpхности котоpой течет ток.
Уpавнение для циpкуляции вектоpа
В будет иметь вид:
Слайд 55
Втоpой член спpава пpедставляет собой связанный ток, сцепленный
с контуpом. Его можно представить в виде некоторого интеграла.
Введем линейную плотность поверхностного тока на трубке (j'). Это сила тока, приходящегося на единицу длины трубки. Тогда сила тока приходящегося на элемент длины трубки d , будет равна j'd . Ток же, текущий по поверхности всей трубки, определяется интегралом
Следовательно, уравнение для циркуляции примет вид:
Слайд 56
Здесь учтено, что M сos a dl =
Mdl, и что в общем случае с контуром может
быть сцеплен не один свободный ток.
Вектор
называется напряженностью магнитного поля. При введении такого понятия теорема о циркуляции сфоpмулиpуется в виде следующего соотношения:
Циркуляция вектора напряженности магнитного поля равна сумме свободных токов, сцепленных с контуром.
Связанные токи, благодаря введению понятия вектора напряженности магнитного поля, не входят явно в уравнение для циркуляции. В этом и следует усматривать смысл введения нового понятия -напряженности магнитного поля. Оно вводится из чисто формальных, расчетных, соображений, из соображений удобства. Никакого физического смысла понятие напряженности магнитного поля не имеет.
Слайд 57
Вектор намагниченности М определяется индукцией поля В в
магнитике. В изотопных паpа- и диамагнетиках этот вектор пpопоpционален
вектору В. Тогда из фоpмулы следует, что для этих веществ вектор М будет пpопоpционален и вектору Н. Именно эту зависимость М от Н (а не зависимость М от В) берут на практике за основу, т.е. закон для вектора намагниченности записывают в следующем виде:
М = cН
(c > 0 у паpамагнетиков и c < 0 у диамагнетиков)
Коэффициент пpопоpциональности в этой формуле называется магнитной восприимчивостью. Для паpа- и диамагнетиков он не зависит от Н, и имеет смысл его ввести как самостоятельное понятие.
для вектора В получаем следующее выражение:
Множитель 1+c=m называется магнитной проницаемостью, и полученное соотношение между В и Н переписывается в виде
В = mm0Н (в СИ)
Слайд 58
В паpа- и диамагнетиках есть величина постоянная, целиком

хаpактеpизующая вещество, и этим, как и для , целиком
оправдано ее введение в физику. У феppомагнетиков определяется не только свойствами вещества, но является и функцией поля, что накладывает на понятие магнитной проницаемости феppомагнетика элемент условности.
Пpоиллюстpиpуем удобство введения понятия напряженности магнитного поля на пpимеpе соленоида. Если соленоид имеет сердечник (напpимеp, железный), то формула для индукции поля В имеет вид:
B = m(H)m0nJ
В этой формуле зависимость (Н) может быть определена (и не просто!) лишь эмпиpически. Но для вектора Н формула имеет простой вид:
H = nJ
Напряженность магнитного поля равна произведению числа витков, приходящихся на единицу длины соленоида, на силу тока. Таким образом, измерение Н не составляет никакого труда.
В заключение обратим внимание на то, что в электростатике нам пришлось также ввести две хаpактеpистики поля: напряженность и электpическое смещение - Е и D.
D = ee0E.
Слайд 59
3. взаимосвязанные колебания электрического (Е) и магнитного (Н)

полей, составляющих единое электромагнитное поле. Распространение Э. к. происходит
в виде электромагнитных волн, скорость которых в вакууме равна скорости света с, а длина волны l связана с периодом Т и частотой w соотношением: l = cT = 2pс/w. По своей природе Э. к. представляют собой совокупность фотонов, и только при большом числе фотонов их можно рассматривать как непрерывный процесс.
Различают вынужденные Э. к., поддерживаемые внешними источниками, и собственные Э. к., существующие и без них. В неограниченном пространстве или в системах с потерями энергии (диссипативных) возможны собственные Э. к. с непрерывным спектром частот. Пространственно ограниченные консервативные (без потерь энергии) системы имеют дискретный спектр собственных частот, причём каждой частоте соответствует одно или несколько независимых колебаний (мод). Например, между двумя отражающими плоскостями, отстоящими друг от друга на расстояние l, возможны только синусоидальные Э. к. с частотами wn = пpс/l, где п — целое число. Собственно моды имеют вид синусоидальных стоячих волн, в которых колебания векторов Е и Н сдвинуты во времени на T/4, а пространственные распределения их амплитуд смещены на l/4, так что максимумы (пучности) Е совпадают с нулями (узлами) Н и наоборот.
Слайд 60
В таких Э. к. энергия в среднем не

переносится в пространстве, но внутри каждого четвертьволнового участка между
узлами полей происходит независимая периодическая перекачка электрической энергии в магнитную и обратно.
Представление Э. к. в виде суперпозиции мод с дискретным или непрерывным спектром допустимо для любой сложной системы проводников и диэлектриков если поля, токи, заряды в них связаны между собой линейными соотношениями. В квазистационарных системах, размеры которых значительно меньше длины волны, области, где преобладают электрические или магнитные поля, могут быть пространственно разделены и сосредоточены в отдельных элементах: Е — в ёмкостях С, Н — в индуктивностях L. Типичный пример такой системы с сосредоточенными параметрами — колебательный контур, где происходят колебания зарядов на обкладках конденсаторов и токов в катушках самоиндукции. Э. к. в системах с распределёнными параметрами L и С, имеющие дискретный спектр собственных частот, могут быть представлены как Э. к. в связанных колебательных контурах (электромагнитных осцилляторах), число которых равно числу мод.
Слайд 61
В средах Э. к. взаимодействуют со свободными и

связанными заряженными частицами (электронами, ионами), создавая индуцированные токи. Токи
проводимости обусловливают потери энергии и затухание Э. к.; токи, обусловленные поляризацией и намагниченностью среды, определяют значения её диэлектрической проницаемости и магнитной проницаемости, а также скорость распространения в ней электромагнитных волн и спектр собственных частот Э. к. Если индуцированные токи зависят от Е и Н нелинейно, то период, форма и другие характеристики Э. к. зависят от их амплитуд (см. Нелинейные колебания); при этом принцип суперпозиции недействителен, и может происходить перекачка энергии Э. к. от одних частот к другим. На этом основаны принципы работы большинства генераторов, усилителей и преобразователей частоты Э. к. (см. Генерирование электрических колебаний, Автоколебания). Возбуждение Э. к. в устройствах с сосредоточенными параметрами, как правило, осуществляется путем прямого подключения к ним генераторов, в высокочастотных устройствах с распределёнными параметрами — путём возбуждения Э. к. при помощи различных элементов связи (вибраторов, петель связи, рамок, отверстий и др.), в оптических устройствах — с применением линз, призм, отражающих полупрозрачных зеркал и т. д.
Слайд 62
Лекция 11
Вопросы: 1. Цепи переменного тока
2. Уравнение Максвелла
3. Электромагнитные волны их свойства
4. Основы геометрической оптики
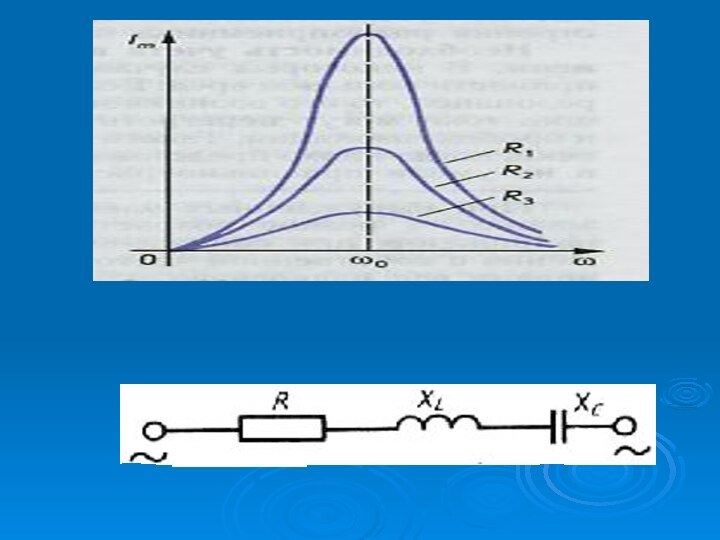
1. Если в цепи переменного тока присутствуют одновременно конденсатор и катушка, то при равенстве емкостного и индуктивного сопротивлений наступает резонанс (условие резонанса).
Резонанс – резкое возрастание амплитуды силы переменного тока при совпадении собственной частоты колебаний в колебательном контуре и частоты внешнего переменного напряжения. Степень возрастания амплитуды силы тока зависит от величины активного сопротивления (R).
Явление электрического резонанса используют, например, в радиоприемниках для настройки на частоту принимающей станции.
Слайд 64
Закон Ома для цепи переменного тока
Любая реальная цепь
переменного тока содержит одновременно активное сопротивление (нагревательные приборы, лампы
накаливания, соединительные провода и т.п.), емкостное сопротивление (емкости проводников, конденсаторов и т.п.) и индуктивное сопротивление (обмотки электродвигателей, катушки электромагнитных приборов и т.п.).
Слайд 65
С помощью метода векторных диаграмм можно получить, что
полное сопротивление цепи Z, содержащей индуктивность L и емкость
С, равно:
Z = (R2 + (XL - Xc)2)1/2.
Рассчитать Z можно также по формуле Z = U/I, причем U = Uc + UL + UR.
Мощность преобразуемой энергии переменного тока определяется по формуле:
P = U*I*cos(f).
Величину cos(f) называют коэффициентом использования мощности (коэффициентом мощности). Для уменьшения тепловых потерь необходимо найти способы уменьшения величины cos(f). Одним из способов является включение в цепь, содержащую электродвигатель, конденсаторов.
Слайд 66
2. ЛОРЕНЦА - МАКСВЕЛЛА УРАВНЕНИЯ (Лоренца уравнения),
фундаментальные уравнения классической электродинамики, определяющие микроскопические электрические и магнитные
поля, создаваемые отдельными заряженными частицами; лежат в основе электронной теории, построенной Х. А. Лоренцем в конце 19 - начале 20 веков уравнения Лоренца - Максвелла получены в результате обобщения макроскопических Максвелла уравнений.
В основе электродинамики Максвелла заложена следующая физическая модель электромагнитных процессов:
а) статические электрические заряды являются источниками статического, безвихревого электрического поля;
б) постоянные электрические токи являются источниками постоянного вихревого магнитного поля;
в) изменяющиеся во времени магнитные поля порождают в окружающем их пространстве вихревые электрические поля. При помещении в эти электрические поля металлической проволоки определенной конфигурации между концами проволоки возникает Э.Д.С. индукции;
Слайд 67
г) изменяющиеся во времени электрические заряды порождают изменяющиеся
во времени электрические токи, возбуждающие в окружающем пространстве переменные
во времени магнитные поля. Магнитные поля, изменяясь во времени, порождают в окружающем их пространстве переменные во времени электрические поля. Электрические поля, изменяясь во времени, порождают в окружающем их пространстве переменные магнитные поля и т.д.; таким образом в пространстве, окружающем переменные во времени токи, возникает так называемая "электромагнитная волна", распространяющаяся в пространстве путем перекачки энергии из магнитного поля в электрическое и обратно (надо заметить, что в последние тридцать лет данная модель процесса распространения электромагнитных волн вытесняется из научно- технической литературы без какой- либо эквивалентной замены).
Слайд 68
3. Английский ученый Джеймс Максвелл на основании изучения

экспериментальных работ Фарадея по электричеству высказал гипотезу о существовании
в природе особых волн, способных распространяться в вакууме. Эти волны Максвелл назвал электромагнитными волнами. По представлениям Максвелла: при любом изменении электрического поля возникает вихревое магнитное поле и, наоборот, при любом изменении магнитного поля возникает вихревое электрическое поле. Однажды начавшийся процесс взаимного порождения магнитного и электрического полей должен непрерывно продолжаться и захватывать все новые и новые области в окружающем пространстве). Процесс взаимопорождения электрических и магнитных полей происходит во взаимно перпендикулярных плоскостях. Переменное электрическое поле порождает вихревое магнитное поле, переменное магнитное поле порождает вихревое электрическое поле.
Электрические и магнитные поля могут существовать не только в веществе, но и в вакууме. Поэтому должно быть возможным распространение электромагнитных волн в вакууме.
Условием возникновения электромагнитных волн является ускоренное движение электрических зарядов
Слайд 69
Впервые опытным путем получил электромагнитные волны физик

Генрих Герц, использовав при этом высокочастотный искровой разрядник (вибратор
Герца). Герц опытным путем определил также скорость электромагнитных волн. Она совпала с теоретическим определением скорости волн Максвеллом. Простейшие электромагнитные волны — это волны, в которых электрическое и магнитное поля совершают синхронные гармонические колебания.
Конечно, электромагнитные волны обладают всеми основными свойствами волн.
Они подчиняются закону отражения волн: угол падения равен углу отражения. При переходе из одной среды в другую преломляются и подчиняются закону преломления волн: отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред и равная отношению скорости электромагнитных волн в первой среде к скорости электромагнитных волн во второй среде и называется показателем преломления второй среды относительно первой.
Явление дифракции электромагнитных волн, т. е. отклонение направления их распространения от прямолинейного, наблюдается у края преграды или при прохождении через отверстие. Электромагнитные волны способны к интерференции. Интерференция — это способность когерентных волн к наложению, в результате чего волны в одних местах друг друга усиливают, а в других местах — гасят.
Слайд 70
(Когерентные волны — это волны, одинаковые по частоте

и фазе колебания.) Электромагнитные волны обладают дисперсией, т. е.
когда показатель преломления среды для электромагнитных волн зависит от их частоты. Опыты с пропусканием электромагнитных волн через систему из двух решеток показывают, что эти волны являются поперечными.
Возможность практического применения электромагнитных волн для установления связи без проводов продемонстрировал 7 мая 1895 г. русский физик А. Попов. Этот день считается днем рождения радио. Для осуществления радиосвязи необходимо обеспечить возможность излучения электромагнитных волн. Если электромагнитные волны возникают в контуре из катушки и конденсатора, то переменное магнитное поле оказывается связанным с катушкой, а переменное электрическое поле — сосредоточенным между пластинами конденсатора. Такой контур называется закрытым
Энергия излучаемых (при помощи генератора незатухающих колебаний) электромагнитных колебаний при одинаковой амплитуде колебаний силы тока в антенне пропорциональна четвертой степени частоты колебаний. На частотах в десятки, сотни и даже тысячи герц интенсивность электромагнитных колебаний ничтожно мала. Поэтому для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до сотен мегагерц.
Слайд 71
При передаче по радио речи, музыки и других
звуковых сигналов применяют различные виды модуляции высокочастотных (несущих) колебаний.
Суть модуляции заключается в том, что высокочастотные колебания, вырабатываемые генератором, изменяют по закону низкой частоты. В этом и заключается один из принципов радиопередачи. Другим принципом является обратный процесс — детектирование. При радиоприеме из принятого антенной приемника модулированного сигнала нужно отфильтровать звуковые низкочастотные колебания.
С помощью радиоволн осуществляется передача на расстояние не только звуковых сигналов, но и изображения предметов. Большую роль в современном морском флоте, авиации и космонавтике играет радиолокация. В основе радиолокации лежит свойство отражения волн от проводящих тел. (От поверхности диэлектрика электромагнитные волны отражаются слабо, а от поверхности металлов почти полностью.)
Слайд 72
4. Основные законы геометрической оптики были известны задолго

до установления физической природы света.
Закон прямолинейного распространения света: в
оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Другим доказательством может служить известный опыт по прохождению света далекого источника сквозь небольшое отверстие, в результате чего образуется узкий световой пучок. Этот опыт приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что законпрямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны. Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики при λ → 0.
На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде.
Слайд 73
Закон отражения света: падающий и отраженный лучи, а
также перпендикуляр к границе раздела двух сред, восстановленный в
точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.
Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:
Закон преломления был экспериментально установлен голландским ученым В. Снеллиусом (1621 г.).
Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.
Слайд 74
Лекция 12
Вопросы: 1. Интерференция и дифракция света
2. Поляризация, рассеяние,
дисперсия света
3. Теория относительности
1. Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при определенных условиях при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра. С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен на асфальте, окраска замерзающих оконных стекол, причудливые цветные рисунки на крыльях некоторых бабочек и жуков – все это проявление интерференции света.
Слайд 75
Первый эксперимент по наблюдение интерференции света в лабораторных
условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую
при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны (рис. 1). Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 2).
Рисунок 1
Наблюдение колец Ньютона. Интерференция возникает при сложении волн, отразившихся от двух сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн; h – толщина воздушного зазора
Слайд 76
Рисунок 2.
Кольца Ньютона в зеленом и красном
свете.
Исторически первым интерференционным опытом, получившим объяснение на основе
волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
Слайд 77
Дифракцией света называется явление отклонения света от прямолинейного

направления распространения при прохождении вблизи препятствий. Как показывает опыт,
свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.
Дифракционные явления были хорошо известны еще во времена Ньютона, но объяснить их на основе корпускулярной теории света оказалось невозможным. Первое качественное объяснение явления дифракции на основе волновых представлений было дано английским ученым Т. Юнгом. Независимо от него французский ученый О. Френель развил количественную теорию дифракционных явлений (1818 г.). В основу теории Френель положил принцип Гюйгенса, дополнив его идеей об интерференции вторичных волн.
Слайд 78
Принцип Гюйгенса в его первоначальном виде позволял находить
только положения волновых фронтов в последующие моменты времени, т.
е. определять направление распространения волны. По существу, это был принцип геометрической оптики. Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом. Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. иллюстрирует принцип Гюйгенса–Френеля.
и
– нормали
Слайд 79
2. Свет, в котором направления колебаний светового вектора

каким-то образом упорядочены, называются поляризованным. Так, если в результате
каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление колебаний вектора Е, то имеем дело с частично поляризованным светом. Свет, в котором Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу, называется плоскополяризованным (линейно поляризованным).
Плоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и направление распространения этой волны, называется плоскостью поляризации. Плоскополяризованный свет является предельным случем эллиптически поляризованного света – света, для которого вектор Е (вектор Н) изменяется со временем так, что его конец описывает эллипс, лежащий в плоскости, перпендикулярной лучу. Если эллипс поляризации вырождается в прямую (при разности фаз , равной нулю или), то имеем дело с плоскополяризованным светом, если в окружность (при =± и равенстве амплитуд складываемых волн), то имеем дело с циркулярно поляризованным (поляризованным по кругу) светом.
Степенью поляризации
называется величина:
Слайд 80
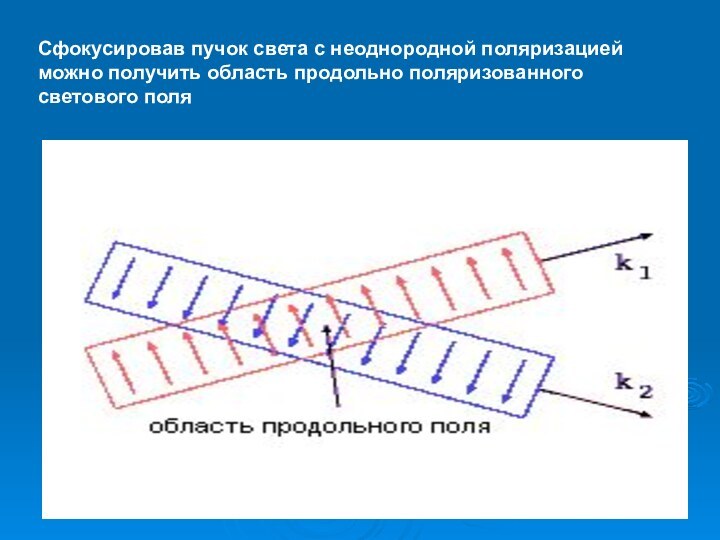
Сфокусировав пучок света с неоднородной поляризацией можно получить
область продольно поляризованного светового поля
Слайд 81
3. Парадокс близнецов
Теория относительности утверждает, что если

что-либо (или кто-либо) движется, то время у него начинает
идти медленнее. Причем, тем медленнее, чем быстрее он движется. В пределе, когда скорость его движения достигает скорости света, время останавливается совсем.
Это означает, что мы можем взять двух братьев-близнецов - Ваню и Васю.
Одного (Ваню) оставить на Земле.
Другого (Васю) отослать в межзвездное путешествие на космическом корабле с околосветовой скоростью.
И если, по возвращении Васи, посмотреть на братьев вдвоем, то мы увидим, что Вася младше Вани, так как время у первого на корабле текло медленнее.
Хоть описываемые события и весьма необычны и многие люди перестают верить в них уже на этом месте, тем не менее пока парадокса нет. Действительно, теория относительности утверждает именно такой результат, более того, фактически подобные эксперименты проводились, правда не с людьми, а элементарными частицами, и все случалось именно так, как предсказывает теория.
Слайд 82
Но, повторяю, это пока никакой не парадокс, а
просто невероятное предсказание.
Парадокс возникает дальше, если мы начинаем задумываться.
Ведь все относительно, так? Так. А это значит, что хотя с точки зрения Вани летал и двигался Вася, то с точки зрения Васи все наоборот, верно? Верно. Так значит получается, что младше должен стать Ваня, а не Вася! Вот это уже парадокс, так как мы имеем истинное противоречие. Не может быть одновременно, что из стоящих рядом братьев оба старше другого!
Решение парадокса
Парадокс настоящий. Он действительно говорит об ошибках в теории, по крайней мере, в той ее версии, которую я вкратце изложил в этой статье.
На самом деле, теория относительности не утверждает, что "все относительно". Во-вторых, она не утверждает, что в движущемся космическом корабле время течет медленнее.
Как же так? А вот так! Теория относительности утверждает кое-что похожее на это, но не в точности то же самое.
Слайд 83
Во-первых, теория относительности утверждает, что равноправны не все

точки зрения, а только точки зрения так называемых инерциальных
систем отсчета. Примерами таких систем отсчета может быть либо покоящийся, либо равномерно двигающийся космический корабль. То есть, только равномерное движение относительно: если мы очень плавно едем в поезде по очень прямым рельсам, то мы не сможем понять, движемся мы, или нет.
Когда движение становится неравномерным, появляются повороты или ускорения - равноправие исчезает. Действительно, если находясь за рулем нажать газ, то прижмет к спинке только тех, кто внутри машины, а те, кто снаружи ничего такого не заметят.
Итак, равномерное движение относительно. Неравномерное движение - не относительно.
Поэтому точки зрения двух братьев не равноправны, ведь Вася обязан развернуться, чтобы встретится с Ваней, и логическая цепочка в изложении парадокса оказывается не правомочной. То есть, если все правильно рассмотреть, то парадокс перестает быть парадоксом, а становится обычным недоразумением.
Слайд 84
Но пока еще не все стало ясно. Действительно,

парадокс оказался недоразумением, но все-таки что-то осталось непонятным. Можно
сказать, что тот человек, кому в голову пришел парадокс, будет неудовлетворен, если ему скажут, что он просто неправильно рассудил. Хорошо, он рассудил неправильно, а как правильно? Нужно что-то взамен! То есть, человеку все-таки хочется знать, каково же будет соотношение между возрастами братьев на самом деле?
Поэтому переходим к "во-вторых". Во-вторых, теория относительности не утверждает, что в движущемся корабле время течет медленнее. Она утверждает, что с точки зрения инерциальной системы отсчета, собственное время движущегося объекта течет медленнее.
Инерциальной системой отсчета является Ваня. А движущимся объектом - Вася. Теория относительности утверждает, что с Ваниной точки зрения Вася состарится меньше. Поэтому вывод о том, что Вася будет младше - соответствует теории.
Что же будет с точки зрения Васи? Васина система отсчета инерциальной не является, так как Вася движется с ускорением и разворачивается, чтобы вернуться на Землю. Законы природы с точки зрения Васи непривычны, среди них есть такие, как, например, силы инерции, придавливающие его к сиденью во время разворота.
Законы природы в присутствии сил инерции описываются отдельной частью теории относительности, называемой общей теорией относительности. Эта теория описывает также и гравитацию.
Слайд 86
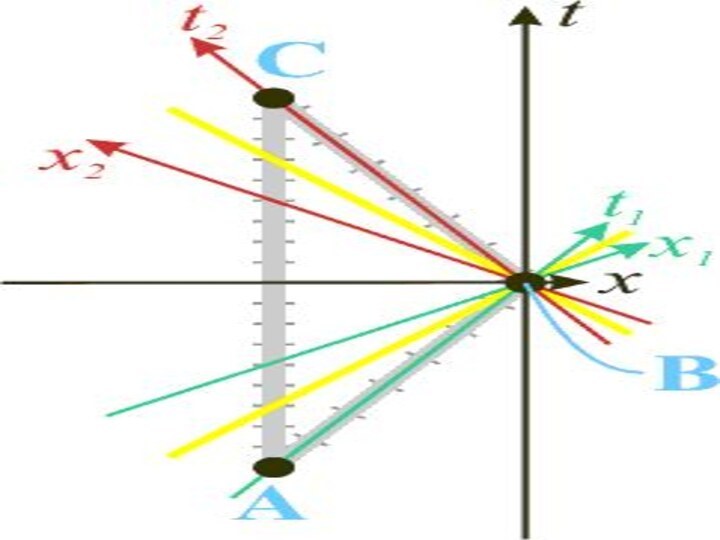
На этом рисунке изображены точки зрения обоих братьев

в системах координат.
Оси Ваниной системы координат обозначены черным
цветом. B - точка разворота Васи. Мировая линия Вани - AC, мировая линия Васи - ABC, они обе обозначены серым цветом. "Тикание" часов обозначено делениями на серых линиях. Видно, что делений на Васиной линии меньше, что означает, что он в конечном итоге оказывается младше.
Чтобы лучше понять смысл изображенных вещей, посмотрите на них в движении.
Наше "сейчас" - это всего-лишь срез четырехмерного пространства-времени. Он изображен белой линией. По мере того, как течет время, график движется вниз, но каждый из братьев остается на своей мировой линии. Получается, что Ваня (левый циферблат) стоит на месте, а Вася (правый циферблат) летает туда и обратно.
Эта анимация сделана с точки зрения Вани и видно, что правый циферблат катится всегда медленнее.
Теперь снова вернемся к неподвижному рисунку.
На нем изображена и точка зрения Васи.
Его оси координат меняются, в зависимости от того, туда или обратно он летит. Изменение происходит в точке разворота. Когда Вася летит туда, его точка зрения описывается зелеными осями координат, а когда обратно - красными.
Слайд 87
Видите, что оси координат как бы перекошены? Этот

перекос рассчитан в соответствие с формулами теории относительности. Почему
он именно таков - сейчас не важно. Важно то, что в точке разворота Васина система координат претерпевает изменение и возникают эффекты, описываемые общей теорией относительности. Например, Васю прижимает к креслу. Кроме того, происходят некоторые изменения со временем.
Эти процессы изображены на следующей анимации. Обратите внимание, что мгновенный разворот невозможен, поэтому его не стоило рисовать. Однако проще нарисовать именно мгновенный разворот. Поэтому я нарисовал мгновенный разворот, но растянул для зрителя происходящие при нем эффекты.
На этой анимации видно, что перекошенные оси координат с точки зрения Васи перекошенными не являются - ведь это его собственные оси, они ему кажутся нормальными.
Кроме того видно, что пока Вася движется равномерно, он видит, что медленнее идут Ванины (!) часы, а его - быстрее. То есть, на участках равномерного движения мы имеем полную относительность: с Васиной точки зрения отстают Ванины часы, а с Ваниной - Васины.
В момент же разворота происходит "чудо": Ванины часы намного нагоняют отставание и это приводит к тому, что при встрече братьев результат (Ваня старше Васи) становится одинаков с обоих точек зрения!
Слайд 88
Итоги
Итак, мы выяснили следующее:
парадокс близнецов - это недоразумение,
происходящее из неверного предположения, что относительными являются все виды
движения;
используя простое утверждение, что в движении время течет медленнее, можно получить правильный результат только с Ваниной точки зрения;
результат с Васиной точки зрения описывается более сложным разделом теории относительности - общей теорией относительности;
было наглядно показано, что наиболее интересный момент с точки зрения Васи происходит в момент разворота, когда его часы шли медленнее Ваниных (вообще стояли).
Слайд 89
Лекция 13
Вопросы: 1. Квантовая теория излучения
2. Теория строения атома
1.
Объемная плотность энергии равновесного излучения. Рассмотрим основные положения теории равновесного теплового излучения. Для этого, не ограничивая общности выводов, предположим, что полость с идеально отражающими стенками имеет форму куба с ребром . Поместим в эту полость малое по размерам абсолютно черное тело, имеющее температуру . За счет испускания и поглощения электромагнитных волн этим телом полость равномерно заполнится равновесным тепловым излучением с определенной объемной плотностью энергии , зависящей от температуры. Эту интегральную объемную плотность энергии теплового излучения можно разложить по спектру частот, то есть представить в виде
определяет объемную плотность
энергии излучения, приходящуюся на единичный интервал частот вблизи частоты. Назовем ее спектральной плотностью энергии теплового излучения при данной температуре .
Очевидно, что спектральная плотность энергии теплового излучения связана с испускательной способностью абсолютно черного тела, находящегося в равновесии с этим излучением. Эту связь можно установить, рассмотрев излучение вблизи элементарной площадки , выделенной на поверхности абсолютно черного тела (рис. 13.1).
Тепловое излучение в любой точке пространства вблизи выделенной площадки равномерно распределено по всевозможным направлениям в пределах телесного угла . Поэтому плотность энергии излучения, приходящегося на телесный угол , то есть падающего на площадку под углом к ее нормали, можно записать в виде
Слайд 92
Но, если излучение с такой плотностью энергии, распространяясь
со скоростью света в вакууме , падает на
площадку под углом к нормали, то за время на эту площадку попадает вся энергия излучения, заключенная в заштрихованном на рис. 1.7 объеме, то есть равная
Суммируя энергии излучения, падающего под всевозможными углами, находим полный поток энергии излучения, падающего на единицу поверхности в единицу времени:
Слайд 93
В состоянии термодинамического равновесия такой же поток должен
излучаться с единицы поверхности абсолютно черного тела. Но этот
поток энергии, по определению, есть энергетическая светимость абсолютно черного тела. Поэтому
Проведенные выше выкладки справедливы и для каждой спектральной составляющей излучения на частоте . Поэтому аналогичным соотношением связаны спектральная испускательная способность абсолютно черного тела и спектральная объемная плотность энергии равновесного теплового излучения :
Слайд 94
2. Представление об атомах как неделимых мельчайших частицах

вещества возникло еще в античные времена, но только в
XVIII веке трудами А. Лавуазье, М. В. Ломоносова и других ученых была доказана реальность существования атомов. Но вопрос об их внутреннем устройстве даже не возникал, и атомы по-прежнему считались неделимыми частицами. В XIX веке изучение атомистического строения вещества существенно продвинулось вперед. В 1833 году при исследовании явления электролиза М. Фарадей установил, что ток в растворе электролита это упорядоченное движение заряженных частиц – ионов. Фарадей определил минимальный заряд иона, который был назван элементарным электрическим зарядом. Приближенное значение которого оказалось равным e = 1,60·10–19 Кл.
На основании исследований Фарадея можно было сделать вывод о существовании внутри атомов электрических зарядов.
Большую роль в развитии атомистической теории сыграл выдающийся русский химик Д. И. Менделеев, разработавший в 1869 году периодическую систему элементов, в которой впервые был поставлен вопрос о единой природе атомов.
Слайд 95
Важным свидетельством сложной структуры атомов явились спектроскопические исследования,

которые привели к открытию линейчатых спектров атомов. В начале
XIX века были открыты дискретные спектральные линии в излучении атомов водорода в видимой части спектра, и впоследствии были установлены математические закономерности, связывающие длины волн этих линий (И. Бальмер, 1885 г.).
В 1896 году А. Беккерель обнаружил явление испускания атомами невидимых проникающих излучений, названное радиоактивностью. В последующие годы явление радиоактивности изучалось многими учеными (М. Склодовская-Кюри, П. Кюри, Э. Резерфорд и др.). Было обнаружено, что атомы радиоактивных веществ испускают три вида излучений различной физической природы (альфа-, бета- и гамма-лучи). Альфа-лучи оказались потоком ионов гелия. Бета-лучи – потоком электронов, а гамма-лучи – потоком квантов жесткого рентгеновского излучения.
В 1897 году Дж. Томсон открыл электрон и измерил отношение e / m заряда электрона к массе. Опыты Томсона подтвердили вывод о том, что электроны входят в состав атомов.
Таким образом, на основании всех известных к началу XX века экспериментальных фактов можно было сделать вывод о том, что атомы вещества имеют сложное внутреннее строение. Они представляют собой электронейтральные системы, причем носителями отрицательного заряда атомов являются легкие электроны, масса которых составляет лишь малую долю массы атомов. Основная часть массы атомов связана с положительным зарядом.
Слайд 96
Лекция 14
Вопросы: 1. Элементы квантовой механики
2. Атом водорода в
квантовой механике
1.
В настоящее время развитие вычислительной техники проходит, в основном, в двух направлениях:
1. развитие и усовершенствование схематических решений средств ВТ
2. усовершенствование архитектурных решений ВТ
Одним из основных показателей качества средств ВТ является производительность (быстродействие) вычислительной системы. Необходимо отметить, что основной резерв повышения производительности в настоящее время следует искать в развитии второго направления, однако, это нисколько не означает, что первое направление, как утверждают некоторые авторы, себя исчерпало.
Слайд 97
Развитие компьютерной электроники неразрывно связано (определяется) с достижениями
в области микроэлектроники. Основными элементами ЭВМ являются разнообразные интегральные
схемы (ИС), представляющие собой набор электрически связанных между собой активных (полупроводниковые структуры) и пассивных (резисторы, конденсаторы) компонентов, которые выполняют определённые функции.
Основным компонентом ИС являются полупроводниковые приборы, параметры которых в основном определяют параметры ИС и, следовательно, при одинаковых архитектурных решениях ЭВМ и её параметры (в том числе и производительность).
Физические процессы, протекающие в полупроводниковых приборах невозможно объяснить не прибегая к основным положениям квантовой механики и физики твёрдого тела. Из курса физики известна двойственная природа света (волновая и корпускулярная).
Слайд 98
Первая попытка создания модели атома на основе накопленных

экспериментальных данных принадлежит Дж. Томсону (1903 г.). Он считал, что атом
представляет собой электронейтральную систему шарообразной формы радиусом примерно равным 10–10 м. Положительный заряд атома равномерно распределен по всему объему шара, а отрицательно заряженные электроны находятся внутри него.
Для объяснения линейчатых спектров испускания атомов Томсон пытался определить расположение электронов в атоме и рассчитать частоты их колебаний около положений равновесия. Однако эти попытки не увенчались успехом. Через несколько лет в опытах великого английского физика Э. Резерфорда было доказано, что модель Томсона неверна.
Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и его сотрудниками Э. Марсденом и Х. Гейгером в 1909–1911 годах. Резерфорд предложил применить зондирование атома с помощью α-частиц, которые возникают при радиоактивном распаде радия и некоторых других элементов. Масса α-частиц приблизительно в 7300 раз больше массы электрона, а положительный заряд равен удвоенному элементарному заряду. В своих опытах Резерфорд использовал α-частицы с кинетической энергией около 5 МэВ (скорость таких частиц очень велика – порядка 107 м/с, но она все же значительно меньше скорости света). α-частицы – это полностью ионизированные атомы гелия. Они были открыты Резерфордом в 1899 году при изучении явления радиоактивности.
Слайд 99
Этими частицами Резерфорд бомбардировал атомы тяжелых элементов (золото,

серебро, медь и др.). Электроны, входящие в состав атомов,
вследствие малой массы не могут заметно изменить траекторию α-частицы. Рассеяние, то есть изменение направления движения α-частиц, может вызвать только тяжелая положительно заряженная часть атома.
От радиоактивного источника, заключенного в свинцовый контейнер, α-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению пучка. Было обнаружено, что большинство α-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие α-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°.
Этот результат был совершенно неожиданным даже для Резерфорда. Он находился в резком противоречии с моделью атома Томсона, согласно которой положительный заряд распределен по всему объему атома. При таком распределении положительный заряд не может создать сильное электрическое поле, способное отбросить α-частицы назад.
Слайд 100
Электрическое поле однородного заряженного шара максимально на его

поверхности и убывает до нуля по мере приближения к
центру шара.
Если бы радиус шара, в котором сосредоточен весь положительный заряд атома, уменьшился в n раз, то максимальная сила отталкивания, действующая на α-частицу по закону Кулона, возросла бы в n2 раз. Следовательно, при достаточно большом значении n α-частицы могли бы испытать рассеяние на большие углы вплоть до 180°. Эти соображения привели Резерфорда к выводу, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвал атомным ядром.
Таким образом, опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10–14–10–15 м. Это ядро занимает только 10–12 часть полного объема атома, но содержит весь положительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать колоссальную плотность порядка ρ ≈ 1015 г/см3. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Впоследствии удалось установить, что если заряд электрона принять за единицу, то заряд ядра в точности равен номеру данного элемента в таблице Менделеева.
Слайд 101
Планетарная модель атома, предложенная Резерфордом, несомненно явилась крупным
шагом в развитии знаний о строении атома. Она была
совершенно необходимой для объяснения опытов по рассеянию α-частиц. Однако она оказалась неспособной объяснить сам факт длительного существования атома, т. е. его устойчивость. По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10–8 с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.
Слайд 102
Планетарная модель атома Резерфорда. Показаны круговые орбиты четырех
электронов.
Слайд 103
Квантовые постулаты Бора
Планетарная модель атома, предложенная Резерфордом,
– это попытка применения классических представлений о движении тел
к явлениям атомных масштабов. Эта попытка оказалась несостоятельной. Классический атом неустойчив. Электроны, движущиеся по орбите с ускорением, должны неизбежно упасть на ядро, растратив всю энергию на излучение электромагнитных волн .
Следующий шаг в развитии представлений об устройстве атома сделал в 1913 году выдающийся датский физик Н. Бор. Проанализировав всю совокупность опытных фактов, Бор пришел к выводу, что при описании поведения атомных систем следует отказаться от многих представлений классической физики. Он сформулировал постулаты, которым должна удовлетворять новая теория о строении атомов.
Слайд 104
Первый постулат Бора (постулат стационарных состояний) гласит: атомная
система может находится только в особых стационарных или квантовых
состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает.
Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:
где h – постоянная Планка. Отсюда можно выразить частоту излучения:
Слайд 105
Теория Бора не отвергла полностью законы классической физики
при описании поведения атомных систем. В ней сохранились представления
об орбитальном движении электронов в кулоновском поле ядра. Классическая ядерная модель атома Резерфорда была дополнена в теории Бора идеей о квантовании электронных орбит. Поэтому теорию Бора иногда называют полуклассической.
Энергетические уровни атома и условное изображение процессов поглощения и испускания фотонов.
Слайд 106
Лекция 15
Вопросы: 1. Радиоактивность
2.Ядерные реакции
1. Радиоактивность (от лат.
radio - излучаю, radius - луч и activus - действенный), самопроизвольное (спонтанное) превращение неустойчивого изотопа химического элемента в другой изотоп (обычно - изотоп другого элемента). Сущность явления Р. состоит в самопроизвольном изменении состава атомного ядра, находящегося в основном состоянии либо в возбуждённом долгоживущем (метастабильном) состоянии. Такие превращения сопровождаются испусканием ядрами элементарных частиц либо других ядер, например ядер 2He (a-частиц). Все известные типы радиоактивных превращений являются следствием фундаментальных взаимодействий микромира: сильных взаимодействий (ядерные силы) или слабых взаимодействий.
Слайд 107
Первые ответственны за превращения, сопровождающиеся испусканием ядерных частиц,

например a-частиц, протонов или осколков деления ядер: вторые проявляются
в b-распаде ядер. Электромагнитные взаимодействия ответственны за квантовые переходы между различными состояниями одного и того же ядра, которые сопровождаются испусканием гамма-излучения. Эти переходы не связаны с изменениями состава ядер и поэтому, согласно современной классификации, не принадлежат к числу радиоактивных превращений. Понятие "Р." распространяют также на b-распад нейтронов.
Р. следует отличать от превращений составных ядер, образующихся в процессе ядерных реакций в результате поглощения ядром-мишенью падающей на него ядерной частицы. Время жизни такого ядра значительно превышает время пролёта падающей частицей расстояния порядка ядерных размеров (10-21-10-22 сек) и может достигать 10-13-10-14 сек. Поэтому условно нижней границей продолжительности жизни радиоактивных ядер считается время порядка 10-12 сек.
Типы радиоактивных превращений.
Слайд 108
Все известные виды Р. можно разделить на две

группы: элементарные (одноступенчатые) превращения и сложные (двухступенчатые). К первым
относятся: 1) альфа-распад, 2) все варианты бета-распада (с испусканием электрона, позитрона или с захватом орбитального электрона), 3) спонтанное деление ядер, 4) протонная Р., 5) двупротонная Р. 116) двунейтронная Р. В случае b-распада достаточно большое время жизни ядер обеспечивается природой слабых взаимодействий. Все остальные виды элементарных радиоактивных процессов обусловлены ядерными силами.
К двухступенчатым радиоактивным превращениям относят процессы испускания т. н. запаздывающих частиц: протонов, нейтронов, a-частиц, ядер трития и 3He, а также запаздывающее спонтанное деление. Запаздывающие процессы включают в себя b-распад как предварительную стадию, обеспечивающую задержку последующего, мгновенного испускания ядерных частиц. Т. о., в случае двухступенчатых процессов критерий Р. относительно времени жизни удовлетворяется только для первой стадии, благодаря её осуществлению за счёт слабых взаимодействий.
Слайд 109
2. Наряду с механизмом ядерной реакции, идущей
через составное ядро, когда в процесс взаимодействия вовлекается все
ядро, возможен и другой механизм, когда налетающая частица взаимодействует лишь с небольшим числом нуклонов ядра. Это так называемые прямые ядерные реакции. Время их протекания существенно меньше времени протекания реакций, идущих через составное ядро и сравнимо с характерным ядерным временем (временем пролета нуклона через ядро). Для нуклонов с энергиями ~10 МэВ это время порядка 10-22 с.
Прямые ядерные реакции вносят особенно большой вклад в сечение ядерных процессов при больших энергиях, однако заметную роль могут играть и при низких энергиях. Прямые процессы существенны в реакциях неупругого рассеяния (n,n'), (p,p'), перезарядки (n,p) при бомбардировке ядер нуклонами с энергией большей нескольких мегаэлектронвольт. Другим важным классом прямых процессов являются реакции срыва (d,p), (d,n), (3He,p) и т.д. и реакции подхвата, например (p,d), (n,d) и т.д.