- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгоритм Краскала
Содержание
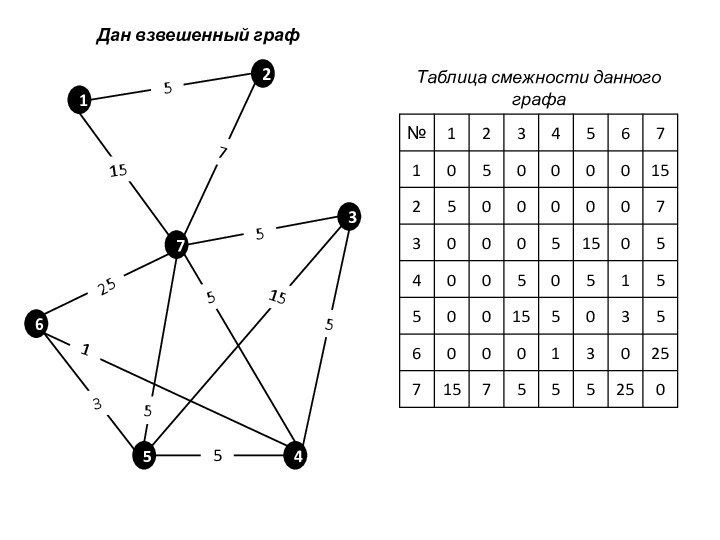
- 2. Таблица смежности данного графаДан взвешенный граф
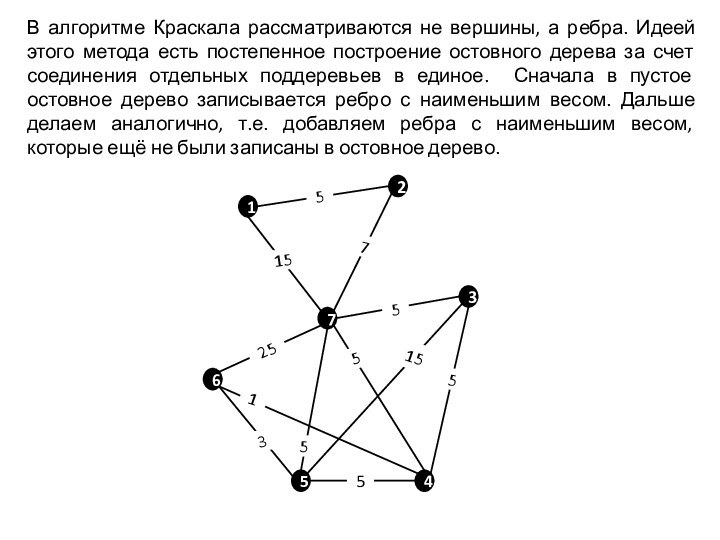
- 3. В алгоритме Краскала рассматриваются не вершины, а
- 4. Алгоритм можно сформулировать так:1. Определяем начально состояние
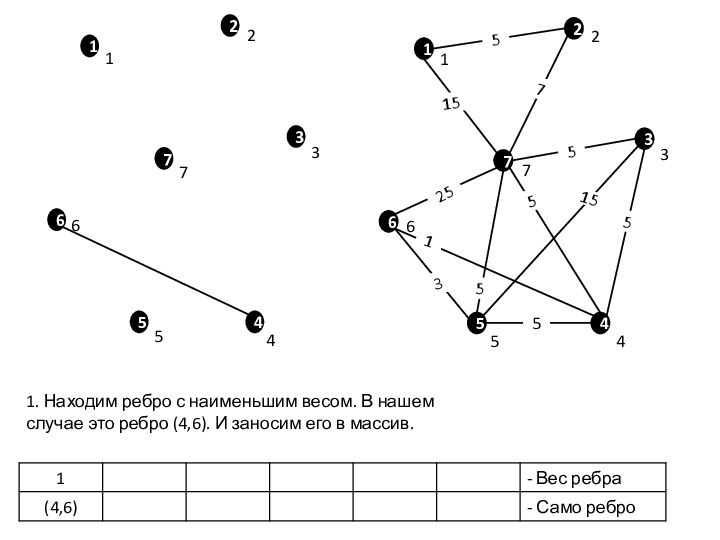
- 5. 1. Находим ребро с наименьшим весом. В
- 6. Дальше мы ищем ребра с наименьшим весом, и действуем аналогично. 1(4,6)3(5,6)555735(1,2)5(3,4)5(3,7)7(2,7)
- 7. Скачать презентацию
- 8. Похожие презентации
Таблица смежности данного графаДан взвешенный граф




Слайд 4
Алгоритм можно сформулировать так:
1. Определяем начально состояние остовного
дерева как пустой и считаем, что все вершины создают
N поддеревьев, которые в свою очередь не имеют никаких ребер. Присвоим им имена порядкового номера соответствующих вершин.2. Если же количество ребер в остовном дереве меньше чем (N-1), то среди свободных ребер данного графа, которые ещё не были задействованы в остовном дереве, определяем ребро с наименьшим весом. Таки ребром может быть ребро, которое принадлежит разным поддеревьям. В другом случаи переходи к пункту 4.
3. Добавляем новое ребро к остовному дереву, а вершинам, которые принадлежат двум поддеревьям, что объединяются, и к оторым принадлежат вершины текущего ребра, присвоить значение порядкового номера одного из поддеревьев.
4. Завершить алгоритм.





























