по теме «Прямоугольный треугольник»;
2) совершенствовать навыки решения задач
на применение свойств прямоугольного треуго-льника, признаков равенства прямоугольных треугольников.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


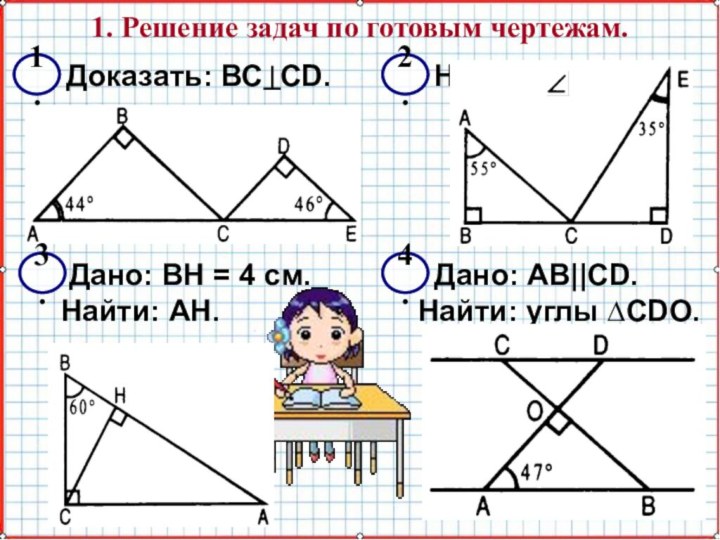
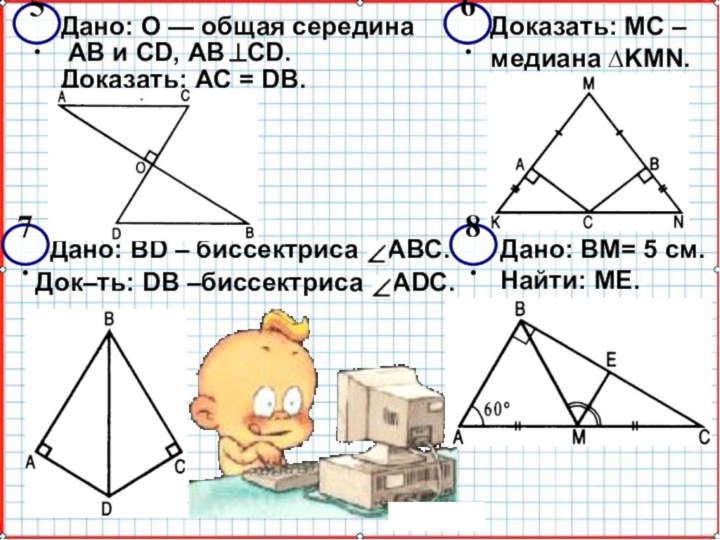





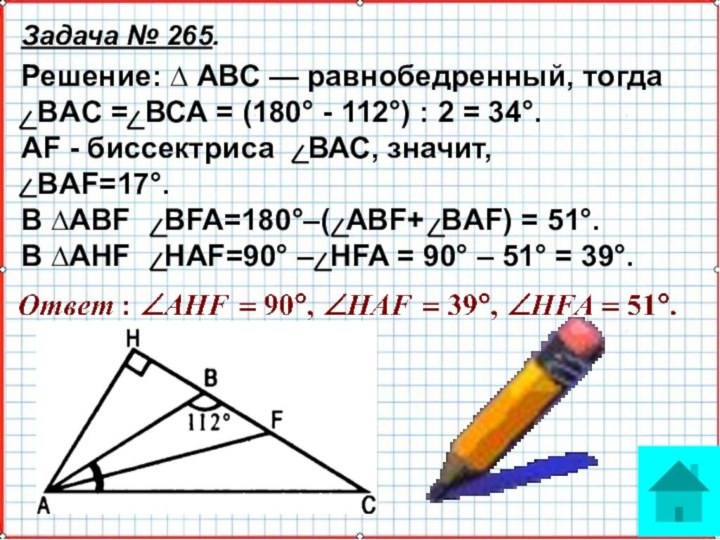

Дано: ВН = 4 см.
Найти: АН.
1.
2.
3.
4.
Доказать: МС –
медиана ∆KMN.
Дано: BD – биссектриса АВС.
Док–ть: DB –биссектриса ADC.
5.
6.
7.
8.
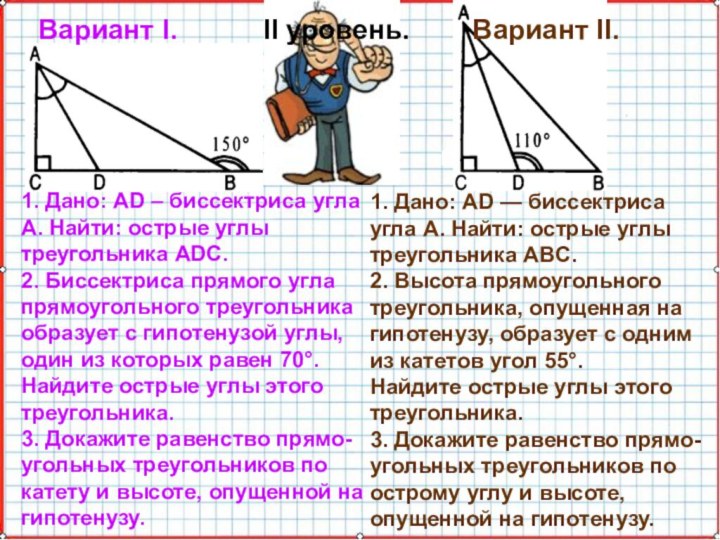
Вариант I. I уровень. Вариант II.
1. Найти острые углы треугольника ABC.
2. Высота остроугольного треугольника ABC образует со сторонами, выходящими из той же вершины, углы 24° и 38°. Найдите углы треугольника ABC.
3. Докажите равенство прямоугольных треуголь-ников по катету и
противолежащему углу.
2. Самостоятельная работа.
1. Дано: AD — биссектриса угла А. Найти: острые углы треугольника ABC.
2. Высота прямоугольного треугольника, опущенная на гипотенузу, образует с одним из катетов угол 55°.
Найдите острые углы этого треугольника.
3. Докажите равенство прямо-угольных треугольников по острому углу и высоте, опущенной на гипотенузу.
Вариант I. II уровень. Вариант II.
1. Дано: ACB= 90°, В = 40°, CD – высота. Найти: острые углы треугольника ACD.
2. Угол между биссектрисой и высотой, проведенными из вершины наибольшего угла прямоугольного треугольника, равен 22°. Найдите острые углы данного треугольника.
3. Докажите равенство остроугольных треугольников по стороне и проведенным к ней медиане и высоте.
1. Дано: ACB= 90°, DCB = 50°, CD – высота. Найти: ост-рые углы треугольника АВС.
2. Угол между биссектрисой и высотой, проведенными из вершины наибольшего угла прямоугольного треугольника, равен 14°. Найдите острые углы данного треугольника.
3. Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.
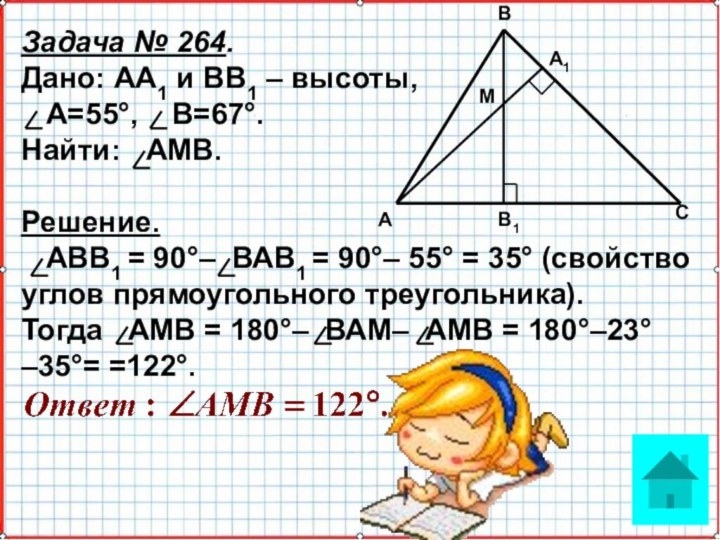
Что и требовалось доказать.