- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Перестановки в задачах комбинаторики в 11 классе
Содержание
- 2. Определение Размещениями из m элементов по n элементов
- 3. Задача 1 Сколько различных двузначных чисел можно записать
- 4. Задача 2 Сколькими способами можно обозначить вершины данного
- 5. Сколько трехзначных чисел, в которых цифры не
- 6. В пассажирском поезде 9 вагонов. Сколькими способами
- 7. Скачать презентацию
- 8. Похожие презентации
Определение Размещениями из m элементов по n элементов (n≤ m) называются такие соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые отличаются одно от другого либо сами ми элементами, либо порядком
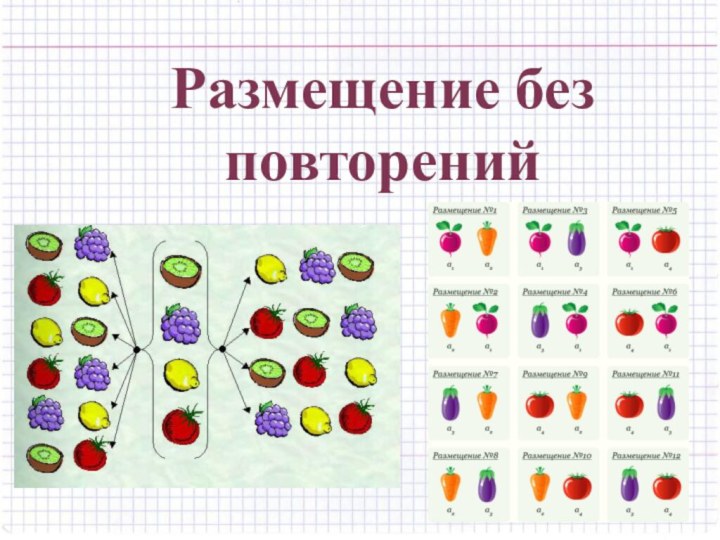






Слайд 3
Задача 1
Сколько различных двузначных чисел можно записать с
помощью цифр 1, 2, 3, 4 при условии, что
в каждой записи нет одинаковых цифр?Решение: перебором убедимся в том, что из четырех цифр 1, 2, 3, 4 можно составить 12 двузначных чисел, удовлетворяющих условию:
12, 13, 14
21, 23, 24
31, 32, 34
41, 42, 43
В записи двузначного числа на первом месте может стоять любая из данных четырех цифр, а на втором – любая из трех оставшихся. По правилу произведения таких двузначных чисел 4×3=12
Слайд 4
Задача 2
Сколькими способами можно обозначить вершины данного треугольника,
используя буквы A, B, C, D, E, F?
Решение: задача
сводится к нахождению числа размещений из 6 элементов по 3 элемента в каждом. Находим А=6×5×4=120, т.е. вершины можно обозначить 120 способами.Слайд 5 Сколько трехзначных чисел, в которых цифры не повторяются,
можно составить из 4 цифр: 1, 2, 3, 4?
Решение: перечислим с помощью схемы все возможные числа:
Видим, что всего данных чисел 4·3·2 = 24.
Слайд 6 В пассажирском поезде 9 вагонов. Сколькими способами можно
рассадить в поезде 4 человека, при условии, что все
они должны ехать в различных вагонах?Решение: т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n=9, m=4. Число таких размещений находим по формуле: A = n ⋅(n − ⋅()1 n − ⋅...)2 ⋅(n − m + )1 m n . Получаем: 9×8×7×6= 3024