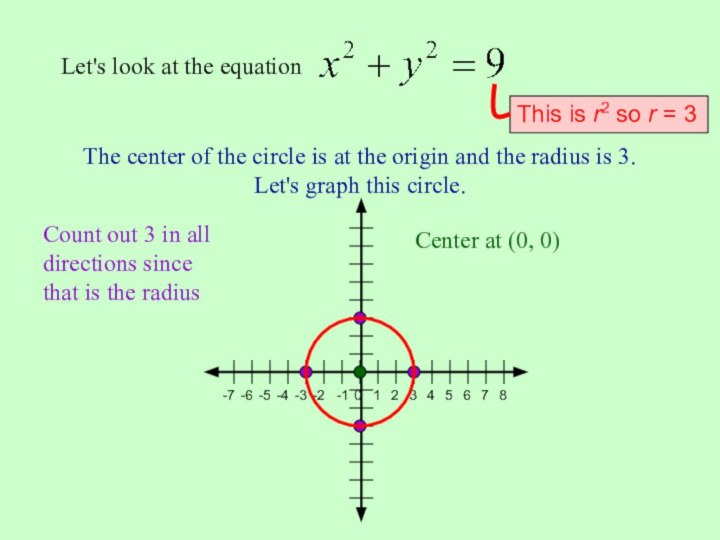
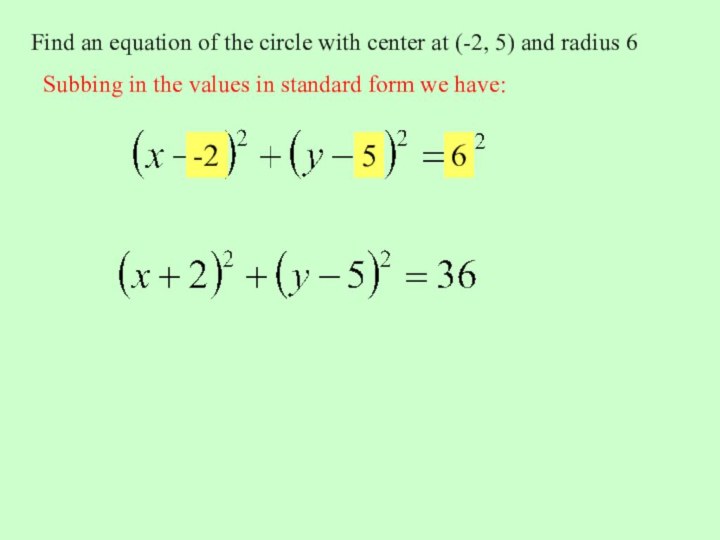circle with its center at the origin is
Notice
that both the x and y terms are squared. Linear equations don’t have either the x or y terms squared. Parabolas have only the x term was squared (or only the y term, but NOT both).r is the radius of the circle so if we take the square root of the right hand side, we'll know how big the radius is.