Слайд 2
Фигуры.
Арбелос
Прямой угол
Двугранный угол Салинон
Единичная окружность Сегмент (геометрия)
Единичный квадрат Сектор (геометрия)
Звёздная область Симплекс
Квадрат Спидроны
Кольцо (геометрия) Срединная ось
Криволинейная трапеция Телесный угол
Круг Трёхгранный угол
Ломаная Треугольник
Луч (геометрия) Угол
Полукруг Шаровой сектор
Полуплоскость
Слайд 3
Арбелос
Арбелос (греч. άρβυλος — сапожный нож) —
плоская геометрическая фигура. На прямой взяты три точки A,
B и C. Построены три полуокружности с диаметрами AB, BC и AC, расположенные по одну сторону от этой прямой. Фигура, ограниченная этими полуокружностями, и называется арбелос.
Площадь арбелоса равна площади круга с диаметром HA.
Отрезок BH пересекает полуокружность BA в точке D. Отрезок CH пересекает полуокружность AC в точке E. Тогда DHEA является прямоугольником.
Прямая DE касается полуокружности BA в точке D и полуокружности AC в точке E.
Слайд 4
Двугранный угол
Двугранный угол — пространственная геометрическая фигура,
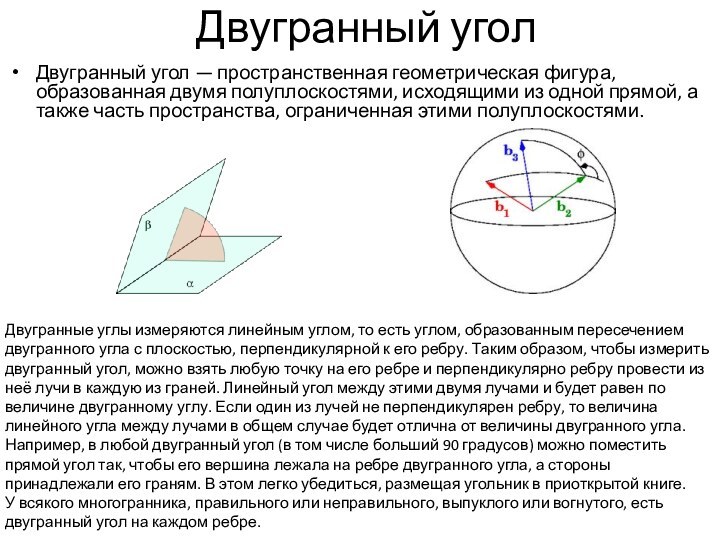
образованная двумя полуплоскостями, исходящими из одной прямой, а также
часть пространства, ограниченная этими полуплоскостями.
Двугранные углы измеряются линейным углом, то есть углом, образованным пересечением двугранного угла с плоскостью, перпендикулярной к его ребру. Таким образом, чтобы измерить двугранный угол, можно взять любую точку на его ребре и перпендикулярно ребру провести из неё лучи в каждую из граней. Линейный угол между этими двумя лучами и будет равен по величине двугранному углу. Если один из лучей не перпендикулярен ребру, то величина линейного угла между лучами в общем случае будет отлична от величины двугранного угла. Например, в любой двугранный угол (в том числе больший 90 градусов) можно поместить прямой угол так, чтобы его вершина лежала на ребре двугранного угла, а стороны принадлежали его граням. В этом легко убедиться, размещая угольник в приоткрытой книге.
У всякого многогранника, правильного или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом ребре.
Слайд 6
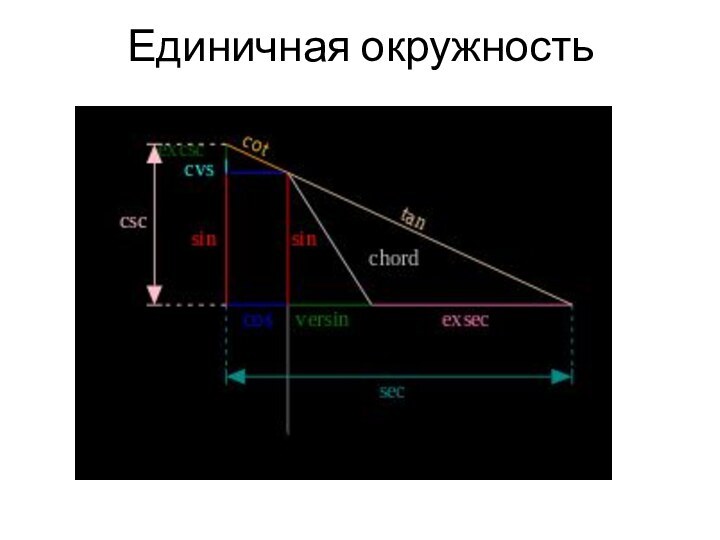
Единичная окружность — это окружность с радиусом 1 и центром в начале координат. Понятие
единичной окружности можно легко обобщить до n-мерного пространства (
). В таком случае используется термин «единичная сфера».
Для всех точек на окружности действительно согласно с теоремой Пифагора:
Синус и косинус могут быть описаны следующим образом: соединив любую точку на единичной окружности с началом координат , мы получаем отрезок, находящийся под углом относительно положительной полуоси абсцисс. Тогда действительно:
Подставив эти значения в вышеуказанное уравнение , мы получаем:
Слайд 7
Единичный квадрат
Единичный квадрат — квадрат в прямоугольных координатах,
левый нижний угол которого находится в начале координат и
имеет длины сторон по единице.
Значит, его вершины имеют координаты , , и . Площадь единичного квадрата — 1, его периметр — 4. Его диагональ равна
Слайд 8
Звёздная область
Звёздная область, относительно фиксированной точки — О область
D евклидов пространства, такая, что отрезок, соединяющий любую
точку области D с точкой O, целиком принадлежит этой области.
Слайд 9
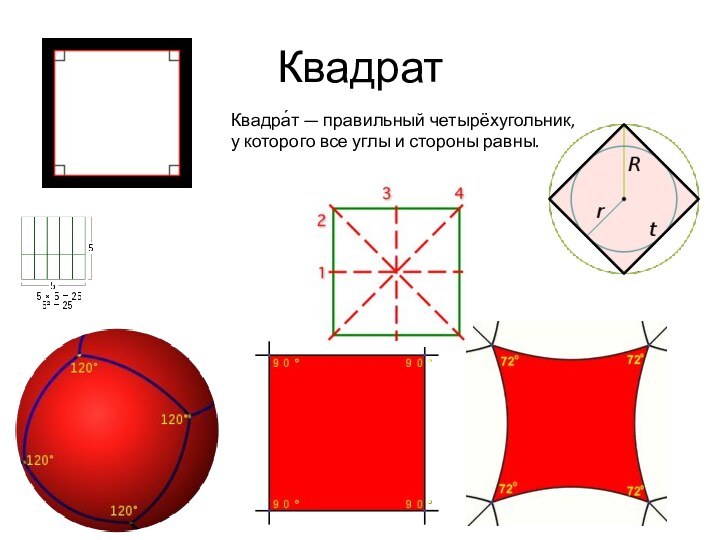
Квадрат
Квадра́т — правильный четырёхугольник, у которого все
углы и стороны равны.
Слайд 10
Кольцо (геометрия)
Кольцо — термин в геометрии, используемый для
описания похожих на кольцо объектов.
Открытое кольцо является топологическим эквивалентом цилиндра
и проколотой плоскости.
Слайд 11
Криволинейная трапеция.
Криволине́йная трапе́ция — плоская фигура, ограниченная графиком неотрицательной непрерывной функции ,
определенной на отрезке [a; b],осью абсцисс и прямыми
и .
Слайд 12
Круг
Круг — геометрическое место точек плоскости, расстояние от
которых до заданной точки, называемой центром круга, не превышает
заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Понятие круга является одним из универсальных математических понятий, дословно обобщаемым на случай произвольных метрических пространств. В отличие от случая евклидовых пространств, при произвольных метриках они могут быть весьма причудливо устроены — в частности, в случае дискретной метрики можно построить пример, когда открытый круг с данным радиусом совпадает с замкнутым. Однако некоторые свойства всё же сохраняются: выпуклость и наличие центральной симметрии.
Слайд 13
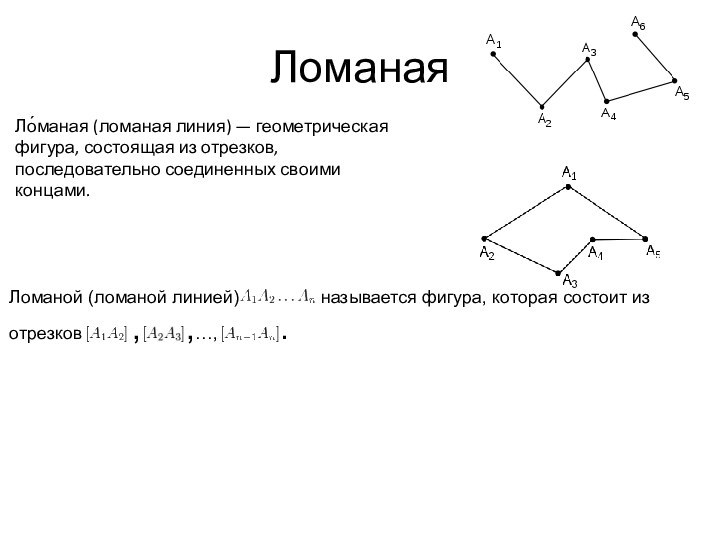
Ломаная
Ло́маная (ломаная линия) — геометрическая фигура, состоящая из
отрезков, последовательно соединенных своими концами.
Ломаной (ломаной линией)
называется фигура, которая состоит из отрезков , ,…, .
Слайд 14
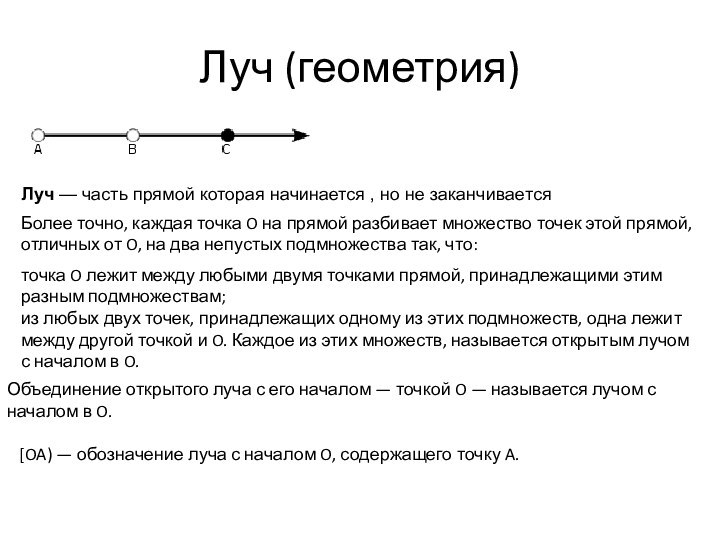
Луч (геометрия)
Луч — часть прямой которая начинается , но
не заканчивается
Более точно, каждая точка O на прямой разбивает
множество точек этой прямой, отличных от O, на два непустых подмножества так, что:
точка O лежит между любыми двумя точками прямой, принадлежащими этим разным подмножествам;
из любых двух точек, принадлежащих одному из этих подмножеств, одна лежит между другой точкой и O. Каждое из этих множеств, называется открытым лучом с началом в O.
Объединение открытого луча с его началом — точкой O — называется лучом с началом в O.
[OA) — обозначение луча с началом O, содержащего точку A.
Слайд 15
Полукруг
Полукруг — сегмент круга, хордой которого является диаметр
этого круга, либо дуга окружности, лежащая между концами диаметра.
Площадь
полукруга составляет одну вторую (3/2) от площади круга с таким же диаметром. Так как полукруг — половина круга 360°, его дуга всегда составляет 180°. Треугольник, вписанный в полукруг, всегда прямоугольный.
Слайд 16
Полуплоскость
Полуплоскость в математике — множество точек плоскости, лежащих
по одну сторону от некоторой прямой на этой плоскости.
Ах
+ By + С > 0, где А, В, С — некоторые постоянные, причём А и В одновременно не равны нулю.
На комплексной плоскости z = х +iy рассматриваются:
верхняя полуплоскость у = Im z > 0,
нижняя полуплоскость у = Im z < 0,
левая полуплоскость х = Re z < 0,
правая полуплоскость x = Re z > 0.
Слайд 17
Прямой угол.
Прямо́й у́гол — угол в радиан или 90°,
половина развернутого угла.
Некоторые геометрические фигуры, у которых один или
несколько углов являются прямыми, имеют собственные названия:
Прямоугольный треугольник — треугольник, у которого один угол прямой.
Прямоугольник — параллелограмм, у которого все углы прямые.
Квадрат — равносторонний прямоугольник, ромб с прямыми углами.
Прямоугольная трапеция — трапеция, хотя бы один из углов которой — прямой.
Слайд 18
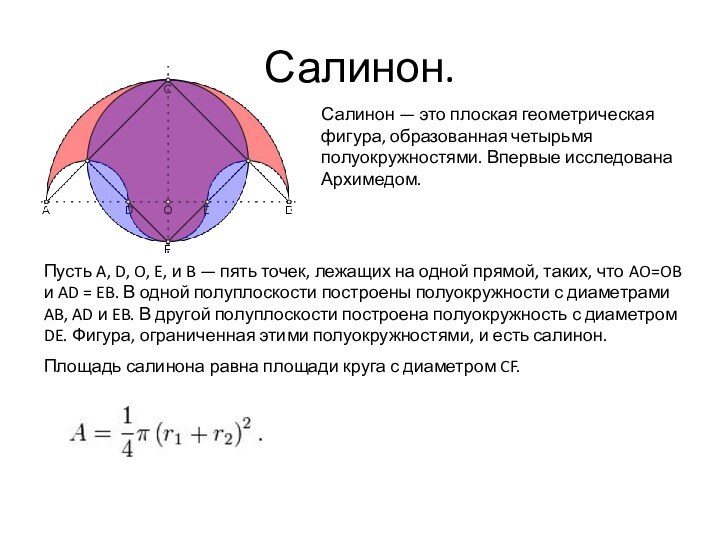
Салинон.
Салинон — это плоская геометрическая фигура, образованная четырьмя
полуокружностями. Впервые исследована Архимедом.
Пусть A, D, O, E, и
B — пять точек, лежащих на одной прямой, таких, что AO=OB и AD = EB. В одной полуплоскости построены полуокружности с диаметрами AB, AD и EB. В другой полуплоскости построена полуокружность с диаметром DE. Фигура, ограниченная этими полуокружностями, и есть салинон.
Площадь салинона равна площади круга с диаметром CF.
Слайд 19
Сегмент (геометрия)
Сегмент — плоская фигура, заключённая между кривой
и её хордой. Как частный случай, круговой сегмент: часть
круга, ограниченная дугой окружности и её хордой или секущей.
Слайд 20
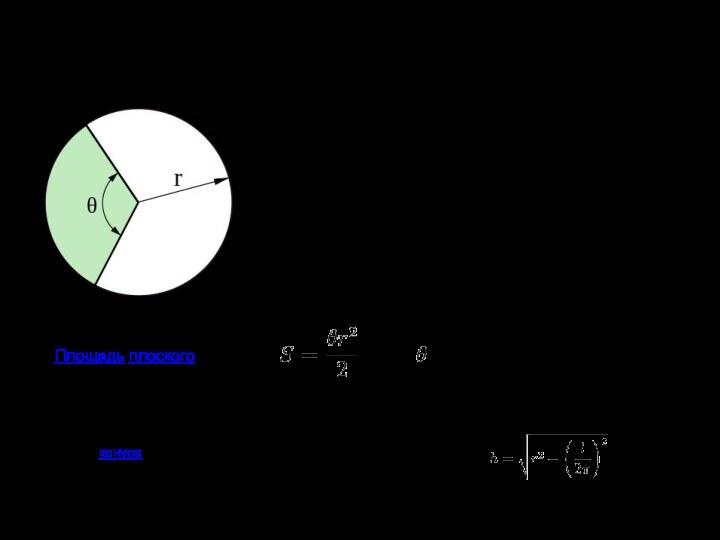
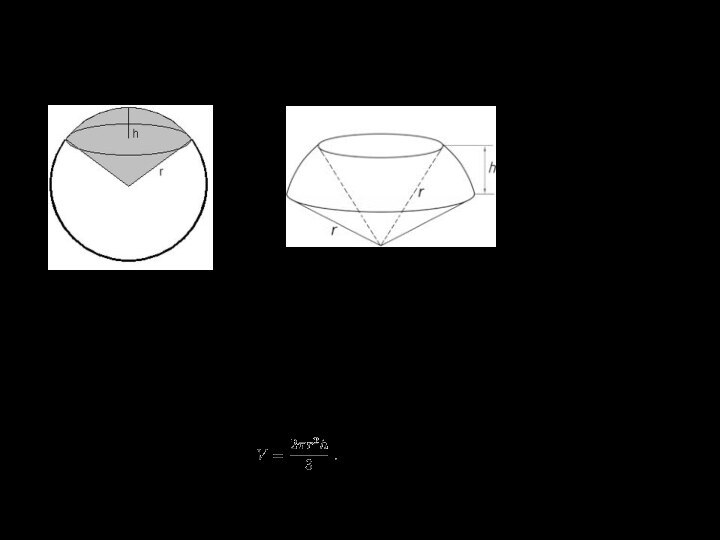
Сектор (геометрия)
Сектор в геометрии — часть круга, ограниченная
дугой и двумя радиусами, соединяющими концы дуги с центром
круга.
Площадь плоского сектора: , где центральный угол в радианах
Высота конуса с боковой поверхностью, образованной сектором:
Слайд 21
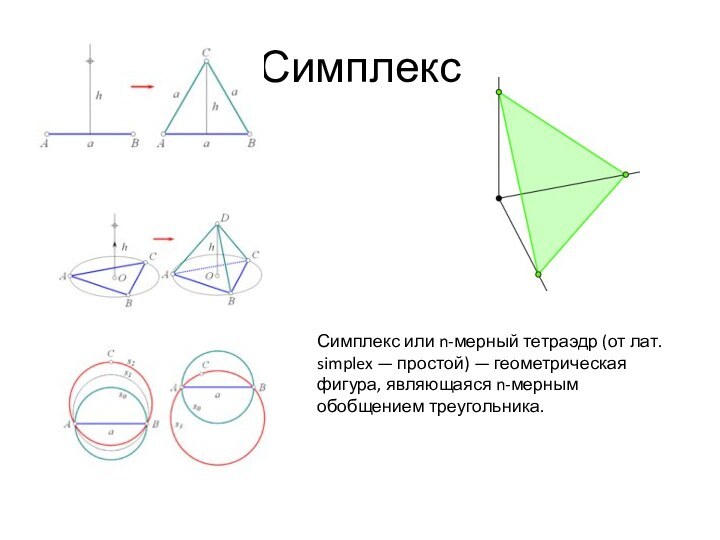
Симплекс
Симплекс или n-мерный тетраэдр (от лат. simplex —
простой) — геометрическая фигура, являющаяся n-мерным обобщением треугольника.
Слайд 22
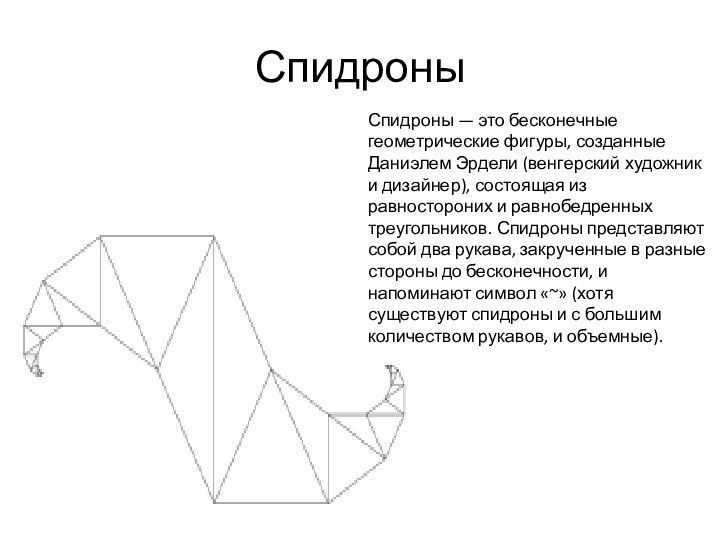
Спидроны
Спидроны — это бесконечные геометрические фигуры, созданные Даниэлем
Эрдели (венгерский художник и дизайнер), состоящая из равностороних и
равнобедренных треугольников. Спидроны представляют собой два рукава, закрученные в разные стороны до бесконечности, и напоминают символ «~» (хотя существуют спидроны и с большим количеством рукавов, и объемные).
Слайд 23
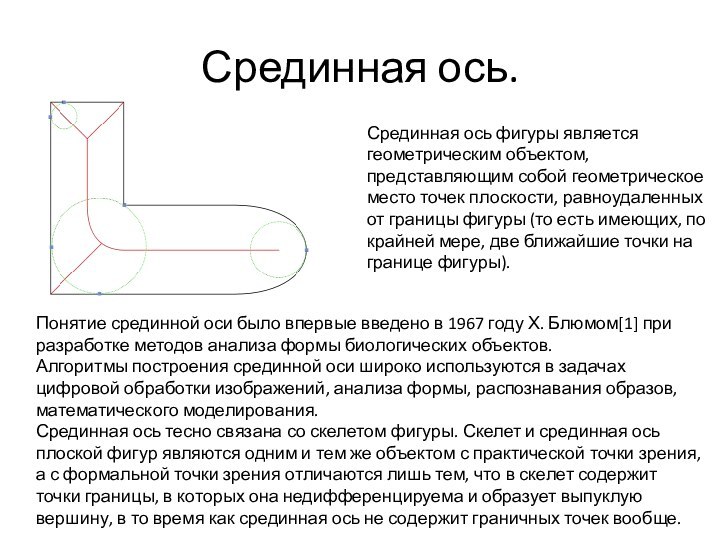
Срединная ось.
Срединная ось фигуры является геометрическим объектом, представляющим
собой геометрическое место точек плоскости, равноудаленных от границы фигуры
(то есть имеющих, по крайней мере, две ближайшие точки на границе фигуры).
Понятие срединной оси было впервые введено в 1967 году Х. Блюмом[1] при разработке методов анализа формы биологических объектов.
Алгоритмы построения срединной оси широко используются в задачах цифровой обработки изображений, анализа формы, распознавания образов, математического моделирования.
Срединная ось тесно связана со скелетом фигуры. Скелет и срединная ось плоской фигур являются одним и тем же объектом с практической точки зрения, а с формальной точки зрения отличаются лишь тем, что в скелет содержит точки границы, в которых она недифференцируема и образует выпуклую вершину, в то время как срединная ось не содержит граничных точек вообще.
Слайд 24
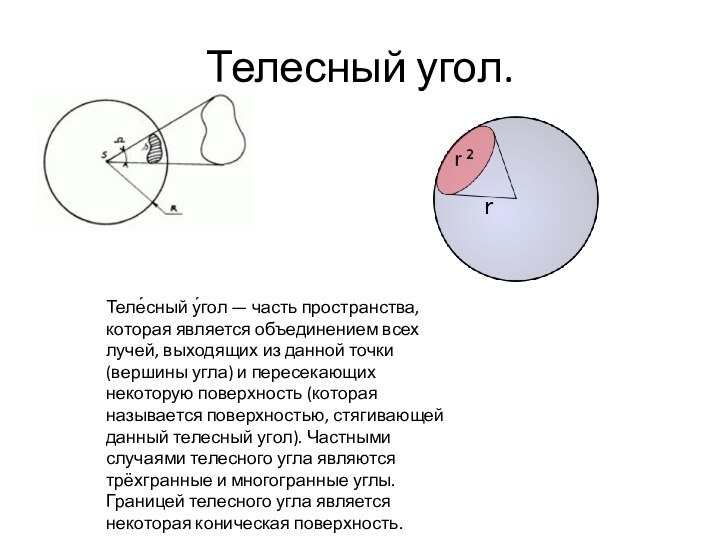
Телесный угол.
Теле́сный у́гол — часть пространства, которая является
объединением всех лучей, выходящих из данной точки (вершины угла)
и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность.
Слайд 25
Трёхгранный угол.
Трёхгранный угол — это часть пространства, ограниченная
тремя плоскими углами с общей вершиной и попарно общими
сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются рёбрами, плоские углы при вершине трёхгранного угла называются его гранями. Каждая из трёх пар граней трёхгранного угла образует двугранный угол (ограниченных третьей гранью, не входящей в пару; при потребности естественным образом снимается это ограничение, в результате чего получаются необходимые полуплоскости, образующие весь двугранный угол без ограничения). Если поместить вершину трёхгранного угла в центр сферы, на её поверхности образуется ограниченный им сферический треугольник, стороны которого равны плоским углам трехгранного угла, а углы — его двугранным углам.
Слайд 26
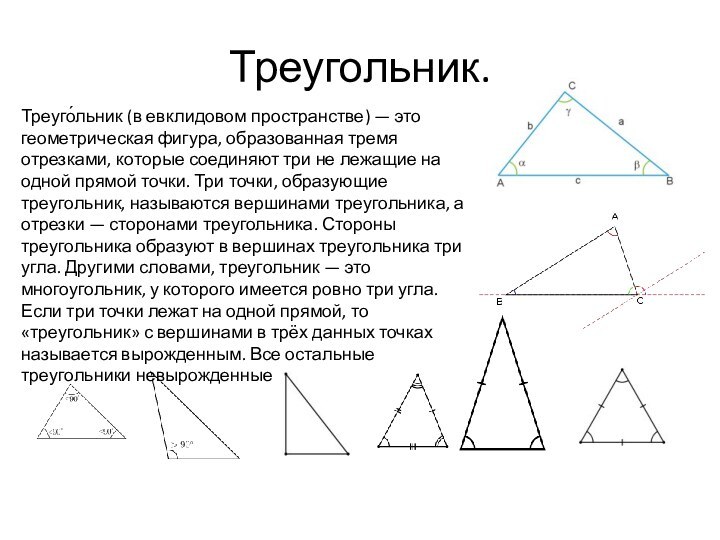
Треугольник.
Треуго́льник (в евклидовом пространстве) — это геометрическая фигура,
образованная тремя отрезками, которые соединяют три не лежащие на
одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.
Слайд 28
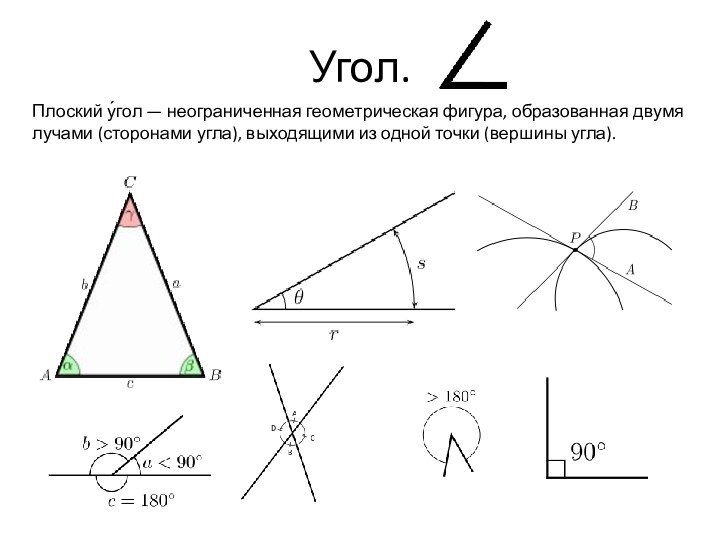
Угол.
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя
лучами (сторонами угла), выходящими из одной точки (вершины угла).