Презентация на тему Фрактальная графика

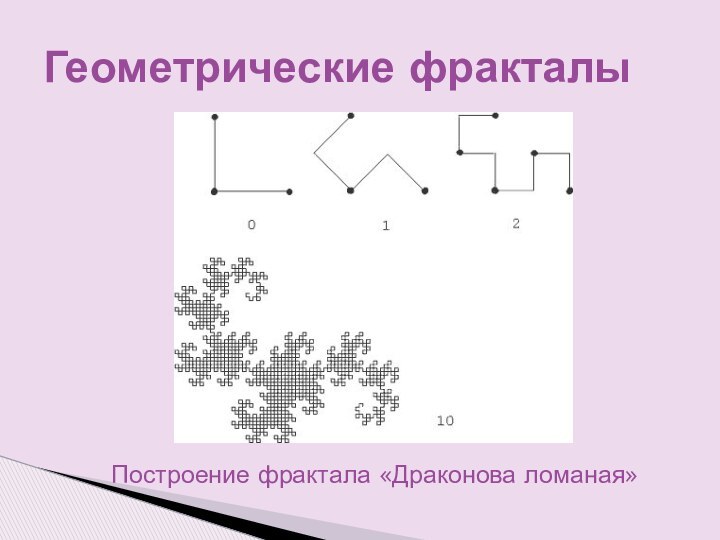
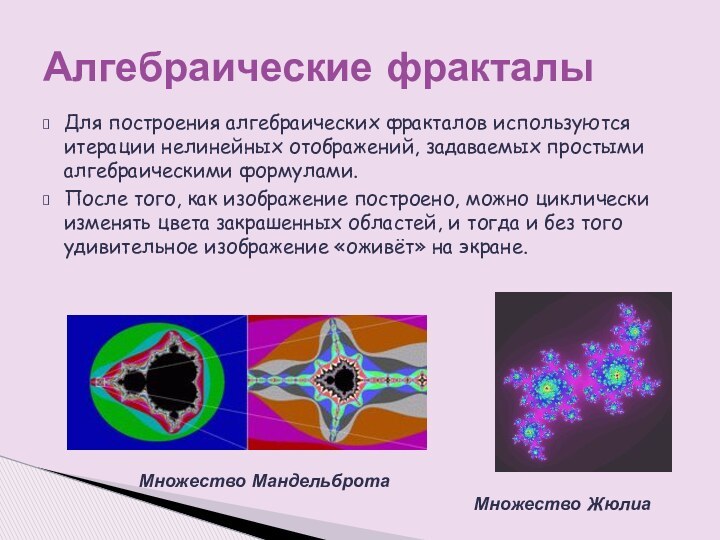
которого наследуют свойства родительских структур.
1977 г. - выход книги

Бенуа Мандельброта  «The Fractal Geometry of Nature» («Фрактальная геометрия природы»). В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф).  
«Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому» (Б. Мандельброт, математический аналитик IBM)

Понятие фрактала

информацию о всём фрактале.
Фрактальная графика незаменима при генерации сложных

неевклидовых объектов, образы которых весьма похожи на природные.

Понятие фрактала

Один из наиболее и знаменитых фрактальных изображений - папоротник, в котором каждый лист в действительности представляет собой миниатюрный вариант самого папоротника

1;
var gd, gm : Integer;
procedure lineto1(x, y

: Integer; l, u : real);
begin
Line(x, y, Round(x + l * cos(u)), Round(y - l * sin(u)));
end;
procedure Draw(x, y : Integer; l, u : real);
begin
if KeyPressed then exit;
if l > min then begin lineto1(x, y, l, u);
x := Round(x + l * cos(u));
y := Round(y - l * sin(u));
Draw(x, y, l*0.4, u - 14*pi/30);
Draw(x, y, l*0.4, u + 14*pi/30);
Draw(x, y, l*0.7, u + pi/30);
end;
end;
begin gd := Detect;
InitGraph(gd, gm, 'c:\bp\bgi');
Draw(320, 460, 140, pi/2);
ReadKey; CloseGraph;
end.

Пример Pascal-программы для рисования фрактального папоротника

 с помощью некоторой ломаной – генератора. За один шаг

алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. 

Геометрические фракталы

самых известных геометрических объектов, описан Хельгой фон Кох в

начале XX века.

Процесс её построения :
берём единичный отрезок, делим на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3.
На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д

это правильный треугольник S0 со стороной 1.
Задаем процедуру, которая

преобразует нулевое поколение: делим средними линиями исходный правильный треугольник на четыре равных треугольника и центральный выбрасываем.
С тремя оставшимися делаем то же самое и так до бесконечности. В результате возникнет убывающая последовательность замкнутых множеств

задаваемых простыми алгебраическими формулами.
После того, как изображение построено, можно

циклически изменять цвета закрашенных областей, и тогда и без того удивительное изображение «оживёт» на экране.

Алгебраические фракталы

Множество Мандельброта

Множество Жюлиа

образом изменяются какие-либо параметры, называются стохастическими. 
Стохастические фракталы
Рандомизированный стохастический фрактал

на основе множества Жюлиа

цвет.
Далее находим центральную точку прямоугольника и раскрашиваем ее

в цвет, равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число.
Чем больше случайное число - тем более "рваным" будет рисунок.

Стохастические фракталы

Типичный стохастический фрактал – «Плазма»

и газе;
Моделирование биологических объектов;
Проектирование антенных устройств;
Алгоритмы сжатия информации (

в т.ч. В компьютерной графике);
Создание текстур в графических программах.

Применение фракталов

программных, так и аппаратных), предназначенных для изображения объёмных объектов. 

Трёхмерное изображение на плоскости включает построение геометрической проекции трёхмерной модели сцены (виртуального пространства моделирования) на плоскость с помощью специализированных программ. 

Понятие трехмерной графики

с помощью различных техник модель;
Материалы - информация о визуальных свойствах

модели (например, цвет стен и отражающая/преломляющая способность окон);
Источники света - настройки направления, мощности, спектра освещения;
Виртуальные камеры - выбор точки и угла построения проекции;
Силы и воздействия - настройки динамических искажений объектов (применяется в основном в анимации);
Дополнительные эффекты - объекты, имитирующие атмосферные явления: свет в тумане, облака, пламя и пр.;

Понятие трехмерной графики

Задача трёхмерного моделирования — описать эти объекты и разместить их в сцене с помощью геометрических преобразований в соответствии с требованиями к будущему изображению.

и линий.
Поверхностная модель — это совокупность поверхностей, ограничивающих и

определяющих трехмерный объект в пространстве. Моделирование поверхностей применяется для детальной отработки вне
Твердотельное моделирование - самое полное и достоверное построение реального объекта. Результатом является монолитный образец объекта, который включает в себя такие компоненты как линии, грани, объем и масса.

Виды 3-D моделирования

полигонов - 862
Этапы 3-D моделирования
Здесь замыкающие объект линии выглядят

более естественными и закругленными. Но это требует большего количества полигонов: 3444.

1 этап – построение каркасной модели

окрашена?
Текстура: 
Ровная ли поверхность или на ней есть вмятины, бугры,

рихтовка или что-то подобное?
Отражающая способность: 
Отражает ли поверхность свет? Четкие ли отражения или они размазаны?

2 этап – определение поверхностных текстур

(shading) и тени (shadow).
Затенение - изменение интенсивности освещения

объекта от одной его стороны к другой. Это создает иллюзию, что объект кроме высоты и ширины имеет еще и глубину.
Иллюзия веса создается вторым эффектом: тенью.

3 этап – настройка освещения

для реалистичного представления неровных (жестких) участков.
«Лесенки» появляются при прорисовке  пиксельного

изображения с помощью прямых линий. 

Прорисовка "серых" пикселей вокруг линий несколько их размывает. Эффект помогает убрать "лесенки" и делает объект более реалистичным.

результат своей работы, компьютер непрерывно строит проекции, отсекает невидимые

грани, просчитывает источники освещения, переводя огромные массивы числовых данных в форму, доступную для восприятия человеческим глазом. Этот процесс называется рендерингом. 
Рендеринг  — процесс получения изображения по модели с помощью компьютерной программы.

Рендеринг

экран без рассмотрения эффекта перспективы относительно наблюдателя.
Метод бросания лучей - сцена

рассматривается, как наблюдаемая из определённой точки. Из точки наблюдения на объекты направляются лучи, с помощью которых определяется цвет пикселя на двумерном экране. Лучи прекращают своё распространение, когда достигают любого объекта сцены либо её фона. 
Трассировка лучей - из точки наблюдения на объекты сцены направляются лучи, с помощью которых определяется цвет пиксела на двумерном экране. Но луч не прекращает своё распространение, а разделяется на три компонента, каждый из которых вносит свой вклад в цвет пиксела отражённый, теневой и преломленный. Количество таких разделений на компоненты определяет глубину трассирования и влияет на качество и фотореалистичность изображения.Метод позволяет получить очень фотореалистичные изображения, но при этом он очень ресурсоёмкий.

Методы рендеринга

и освещения