Презентация на тему Геометричні перетворення9 клас

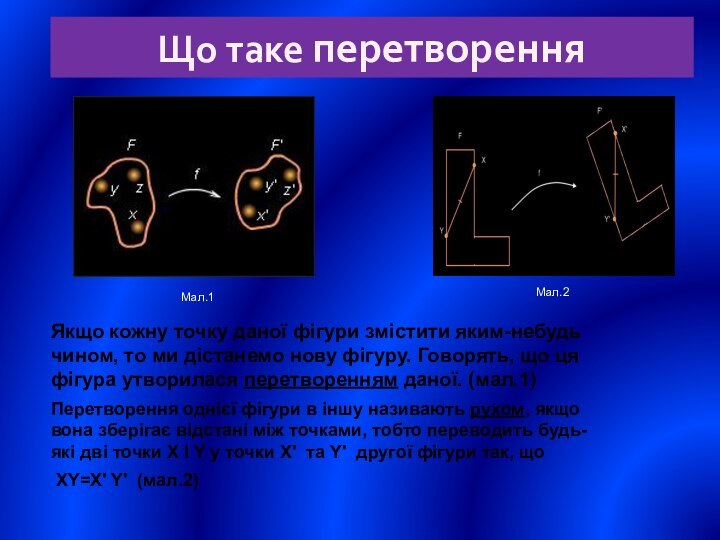
яким-небудь чином, то ми дістанемо нову фігуру. Говорять, що

ця фігура утворилася перетворенням даної. (мал.1)
Перетворення однієї фігури в іншу називають рухом, якщо вона зберігає відстані між точками, тобто переводить будь-які дві точки X I Y у точки X' та Y' другої фігури так, що
XY=X' Y' (мал.2)

Х – довільна точка площини (мал.2). Відкладемо на продовженні

відрізка ОХ за точку О відрізок ОХ’, що дорівнює ОХ. Точка Х’ називається симетричною точці X відносно точки O. Точка, симетрична точці О, є сама точка О. Очевидно , точка симетрична точці X’, є точка Х.

F’, при якому кожна її точка X переходить у

точку X’, симетричну відносно даної точки О, називається перетворенням симетрії відносно точки О. При цьому фігури F і F’ називаються симетричними відносно точки О.
Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то вона називається центральносиметричною, а точка О називається центром симетрії.

Симетрія відносно точки

•

F

F′

O

X′

X

рухом
Доведення:
Нехай X і Y – дві довільні точки фігури

F. Перетворення симетрії відносно точки О переводить їх у точки X’ і Y’. Розглянемо трикутники XOY і X’OY’. Ці трикутники рівні за першою ознакою рівності трикутників. У них кути при вершині О рівні, як вертикальні, а OX=OX’, OY=OY’ за означенням симетрії відносно точки О.

З рівності трикутників випливає рівність сторін XY=X’Y’. А це означає, що симетрія відносно точки О є рух. Теорему доведено.

Зміст

довільну точку Х і опустимо перпендикуляр АХ на пряму

g. На продовженні перпендикуляра за точку А, відкладемо відрізок AX’, що дорівнює відрізку AX. Точка X’ називається симетричною точці X відносно прямої g. Якщо точка Х лежить на прямій g, то симетрична їй точка є сама точка X. Очевидно, що точка симетрична точці X’, є точка Х.

кожна її точка Х переходить у точку X’, симетричну

відносно даної прямої g, називається перетворенням симетрії відносно прямої g. При цьому фігури F і F’ називаються симетричними відносно прямої g.

Симетрія відносно прямої

Зміст

g

F

F′

X

X′

при якому кожний промінь , що виходить з даної

точки, повертається на один і той самий кут в одному і тому самому напрямі. Це означає, що коли при повороті навколо точки О точка Х переходить у точку Х’, то промені ОХ та ОХ‘ утворюють один і той самий кут, якою б не була точка Х. Цей кут називається кутом повороту. Перетворення фігур при повороті площини також називається поворотом.

ПОВОРОТ

Зміст

•

O

X

X′

координати x, y. Перетворення фігури F при якому довільна

точка (х; у) переходить у точку (х+а; у+b), де а і b одні й ті самі для всіх точок (х; у), називається паралельним перенесенням. Паралельне перенесення задається формулами:

Паралельне перенесення

перенесенні точки зміщуються вздовж прямих (або прямих, які збігаються)

на одну й ту саму відстань.

Паралельне перенесення

Зміст

фіксована точка. Через довільну точку Х фігури F проведемо

промінь ОХ і відкладемо на ньому відрізок ОХ’, що дорівнює k·OX, де k – додатне число. Перетворенням фігури F, при якому кожна її точка Х переходить у точку Х’, побудовану таким способом, називається гомотетією відносно центра О. Число k називається коефіцієнтом гомотетії, фігури F і F’ називаються гомотетичними.

ГОМОТЕТІЯ

Зміст

•

O

F

F′

X

X′