Презентация на тему корреляции

вероятностной связи между двумя переменными, измеренными в количественной шкале.

Примером вероятностной связи является связь между ростом и весом людей. Ясно, что один и тот же рост может быть у людей разного веса, как и наоборот.

до 1. Крайние значения соответствуют линейной функциональной связи между

двумя переменными, 0 — отсутствию связи.
Для словесного описания коэффициента корреляции используют следующие градации:

< г < 1. Положительную корреляцию следует интерпретировать следующим

образом: если значения одной переменной возрастают, то значения другой имеют тенденцию к возрастанию. Чем коэффициент корреляции ближе к 1, тем сильнее эта тенденция, и обратно, с приближением коэффициента корреляции к 0 тенденция ослабевает.
Примером значительной положительной корреляции служит зависимость между ростом и весом человека. Считается, что в этом случае коэффициент корреляции равен г = 0,83. Слабая положительная корреляция (г = 0,12) наблюдается между способностью человека к сочувствию и реальной помощью, которую он оказывает нуждающимся людям.
Отсутствие корреляции (no correlation) определяется значением г = 0. Нулевой коэффициент корреляции говорит о том, что значения переменных никак не связаны друг с другом. Примером пары величин с нулевой корреляцией является рост человека и результат его IQ-теста.

Отрицательная корреляция соответствует значениям -1 < г < 0. Если значения одной переменной возрастают, то значения другой имеют тенденцию к убыванию. Чем коэффициент корреляции ближе к -1, тем сильнее эта тенденция, и обратно, с приближением коэффициента корреляции к 0 тенденция ослабевает.
Слабая отрицательная корреляция (г- -0,13) наблюдается между агрессивностью человека по отношению к своему другу и помощью, которую он ему оказывает. Чем агрессивней человек, тем помощь меньше, однако зависимость выражена слабо. Примером значительной отрицательной корреляции (г = -0,73) служит зависимость между нервной возбудимостью человека и его эмоциональной уравновешенностью. Чем выше оказывается результат его теста па возбудимость, тем более низкий результат имеет его тест на уравновешенность.

шкалы, к которой относятся переменные.

Переменные с интервальной

и с номинальной шкалой: коэффициент корреляции Пирсона.

По меньшей мере, одна из двух переменных имеет порядковую шкалу: ранговая корреляция по Спирману или т (тау) Кендала.

Одна из двух переменных является дихотомической: точечная двухрядная корреляция. Эта возможность в SPSS отсутствует. Вместо этого может быть применён расчёт ранговой корреляции.

Обе переменные являются дихотомическими: четырёхполевая корреляция. Данный вид корреляции рассчитываются в SPSS на основании определения мер расстояния и мер сходства

Correlate... (Корреляция)

Bivariate... (Парные)
Появится диалоговое окно Bivariate Correlations (Парные корреляции)

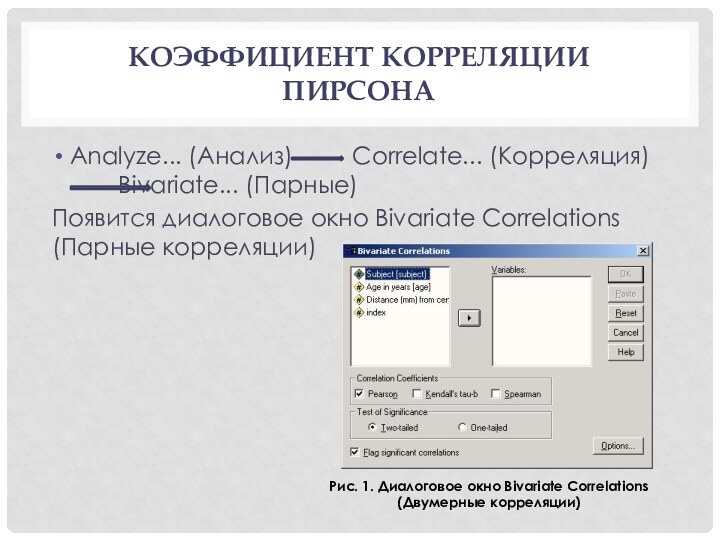
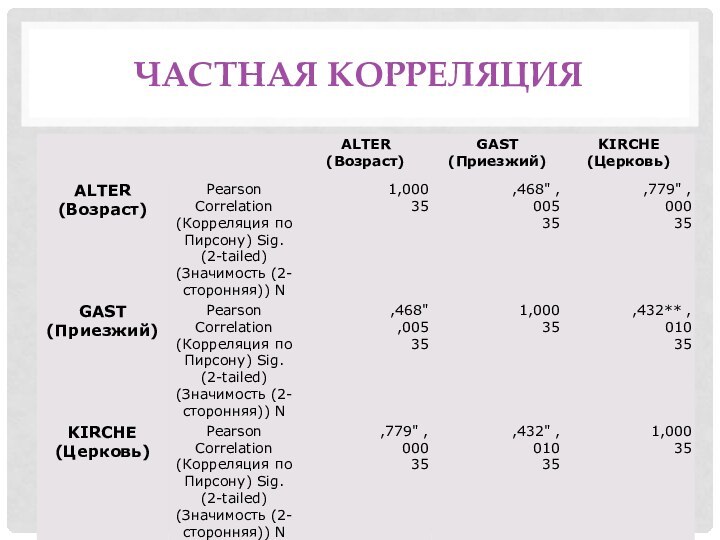
Рис. 1. Диалоговое окно Bivariate Correlations (Двумерные корреляции)

the 0.01 level (2-tailed). (Корреляция является значимой на уровне

0,01 (2-сторонняя)

принадлежащих к порядковой или интервальной шкале вместо коэффициента Пирсона

рассчитывается ранговая корреляция по Спирману.

Для этого отдельным значениям переменных присваиваются ранговые места. Чтобы выявить ранговую корреляцию, уберите в диалоговом окне Bivariate Correlations... (Парные корреляции) метку для расчета корреляции по Пирсону, установленную по умолчанию. Вместо этого активируйте расчет корреляции Спирмана.

Ещё одним вариантом ранговых коэффициентов корреляции являются коэффициенты Кендала (tb Кендала), расчет которых можно вызвать в диалоговом окне Bivariate Correlations... (Парные корреляции). В этом методе одна переменная представляется в виде монотонной последовательности в порядке возрастания величин; другой переменной присваиваются соответствующие ранговые места. Количество инверсий (нарушений монотонности по сравнению с первым рядом) используется в формуле для корреляционных коэффициентов. Применение коэффициента Кендала является предпочтительным, если в исходных данных встречаются выбросы.

сопоставить размер их обуви с уровнем образованности, то между

этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.
В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.

отношение населения к приезжим рабочим-иностранцам. Для этого было сформулировано

несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причём большее значение соответствует более негативному отношению к приезжим рабочим.

Среди многочисленных дополнительных переменных учитывались: возраст опрашиваемых и частота посещения церкви. Последней характеристике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю).

Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из переменных, а именно частота посещения церкви, имеет порядковую шкалу):

Частная корреляция

к примеру, таким образом, что частые посещения церкви коррелируют

с отрицательным отношением к приезжим рабочим (r = 0,432). Прежде, чем поставить в упрёк церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с частотой посещения церкви (r = 0.779). Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.

Частная корреляция

(Частная)

Откроется диалоговое окно Partial Correlations (Частные корреляции).

Оставьте предварительную установку для двухстороннего теста значимости.
При помощи щелчка на кнопке Options... (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).

В случае одной искажающей переменной, как в приведенном примере, возможен расчёт частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдаёт корреляции высших порядков.

Начните расчёт щелчком на кнопке ОК. Вязкие просмотра появится следующий результат:

Частная корреляция