Слайд 2
Экономический подход к определению величины затрат производства
Экономический подход
к определению величины затрат производства несколько отличается от бухгалтерского.
Суть экономического подхода выражается концепцией альтернативных затрат (отвергнутых возможностей). Отправная точка этой концепции состоит в следующем предположении:
а) запасы ресурсов, доступные для вовлечения в производство, ограничены;
б) имеется несколько возможностей применения для всех (или почти для всех) ресурсов.
Слайд 3
Альтернативные затраты
Предположим для простоты, что предприятие приобретает ресурсы
по свободным рыночным ценам, отражающим альтернативные затраты. Будут ли
последние в этом случае равны денежным затратам? Оказывается, что это происходит не всегда. Дело в том, что наряду с явными затратами (на материалы, оборудование, рабочую силу и т.д.), приобретаемые предприятием на стороне, могут существовать и неявные затраты (стоимость затраченных ресурсов, являющихся собственностью фирмы). К последним относятся труд предпринимателя-собственника, процент на вложенный им капитал и т.д.
Слайд 4
Функция затрат
В дальнейшем, говоря о затратах, мы всегда
будем иметь в виду альтернативные затраты как сумму явных
(тождественных бухгалтерским) и неявных затрат.
Теперь, зная, что такое затраты, мы можем приступить к определению функциональной зависимости затрат от объема произведенной продукции, т.е. к построению функции затрат:
С=f(Q)
где Q - количество единиц произведенной продукции;
С - величина затрат, руб.
Слайд 5
Постоянные и переменные затраты
С этой точки зрения величина
затрат может быть разделена на две составляющие.
1. Постоянные затраты (FC),
которые не зависят от объема выпуска продукции. Например, затраты на эксплуатацию зданий, сооружений и оборудования, административно-управленческие расходы, арендная плата, некоторые виды налогов и т.д. Следует отметить, что неявные затраты выступают чаще всего как постоянные.
2. Переменные затраты (VС), изменяющиеся с изменением объема производства. Сюда относятся затраты на материалы, рабочую силу и т.д.
Слайд 6
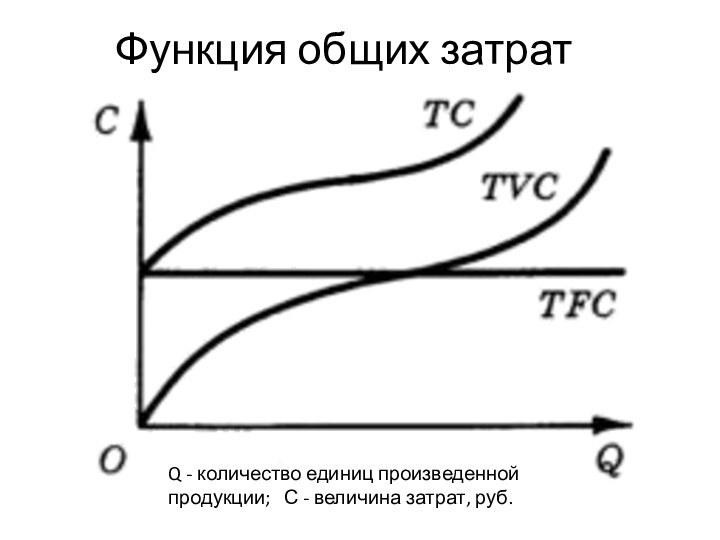
Общие затраты на производство
Тогда общие затраты на производство Q единиц продукции равны сумме
общих постоянных и общих переменных затрат:
TC(Q) =TFC + TVC(Q)
где TC
(Q) - общие затраты при производстве Q единиц продукции;
TFC - общие постоянные затраты;
TVC (Q) - общие переменные затраты при производстве Q единиц продукции.
Слайд 7
Функция общих затрат
Q - количество единиц произведенной продукции;
С - величина затрат, руб.
Слайд 8
Функция средних затрат
Однако производителя часто интересует величина не столько
общих, сколько средних затрат (так как за увеличением первых может скрываться
снижение вторых).
Средние общие затраты есть частное от деления общих затрат на объем выпуска продукции:
АTС = TC/Q = TFC/Q + TVC/Q = AFC + AVC
где AFC - средние постоянные затраты при производстве Q единиц продукции;
AVC - средние переменные затраты при производстве Q единиц продукции.
Слайд 9
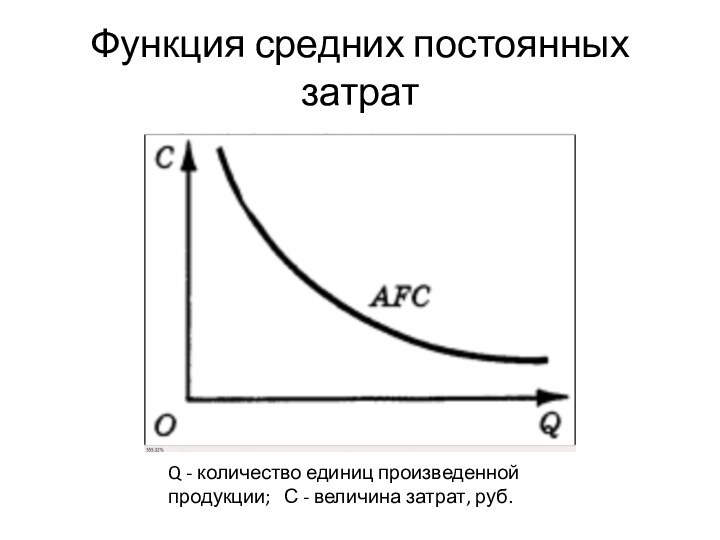
Функция средних постоянных затрат
Рассмотрим сначала функцию средних постоянных затрат.
Поскольку TFC =
const, а AFC = TFC/Q то
график рассматриваемой функции имеет вид
гиперболы
Когда выпускается малое число единиц продукции, на них падает вся тяжесть постоянных затрат. При увеличении объема производства средние постоянные затраты снижаются и величина их стремится к нулю.
Слайд 10
Функция средних постоянных затрат
Q - количество единиц произведенной
продукции; С - величина затрат, руб.
Слайд 11
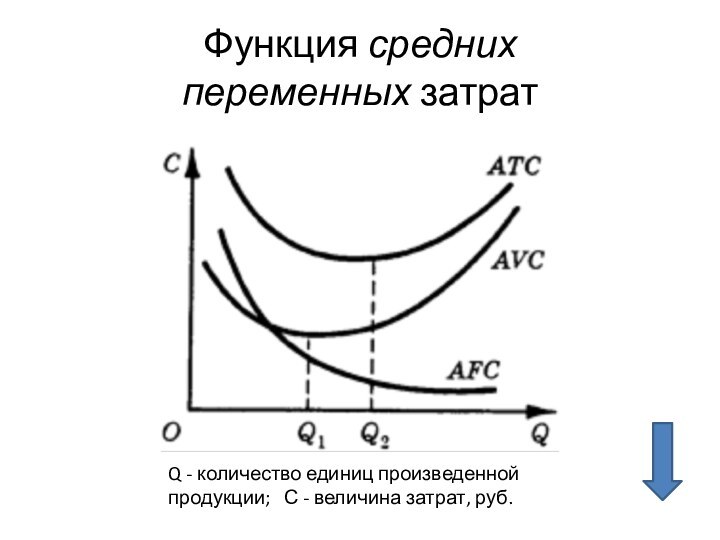
Функция средних переменных затрат
Характер функции средних переменных затрат не может быть обоснован
так же просто, как и функции AFC, и определение его
требует некоторых умозрительных предположений.
Традиционно применяемый вид функции AVC и соответственно функции АTС выводится из так называемого закона убывающей производительности.
Слайд 12
Функция средних переменных затрат
Q - количество единиц произведенной продукции;
С - величина затрат, руб.
Слайд 13
Характер зависимости средних переменных затрат
Предполагается, что
если есть хотя бы один постоянный ресурс (количество которого
не может быть изменено), то при увеличении переменных затрат на прочие ресурсы средняя производительность переменных ресурсов сначала возрастает (средние переменные затраты падают), а затем, начиная с некоторого выпуска Q1, производительность снижается (средние переменные затраты растут).
Слайд 14
Интерпретация характера зависимости средних переменных затрат
Пусть имеется
магазин, в котором работает один работник (хозяин). Он принимает
товар, оформляет витрину, выписывает чеки, обслуживает покупателей и т.д.
С ростом оборота он нанимает грузчика, кассира, продавца, дизайнера, производительность увеличивается за счет разделения труда.
Однако размер магазина фиксирован, и когда нанимается третий грузчик (или второй кассир), производительность падает.
Такая аргументация кажется многим экономистам фантастичной, они оспаривают ее, предлагая альтернативные функции затрат или вовсе отказываясь от них.
Наука развивается, но поразительно, что функции затрат столь простого вида позволяют понять в первом приближении важнейшие экономические зависимости.
Слайд 15
Вид кривой средних общих затрат
Вид кривой средних общих
затрат АTС определяется:
а) видом кривой AVC средних переменных затрат
построенной исходя из закона убывающей производительности;
б) видом кривой AFC средних постоянных затрат. Вспомним, что AFC = АTС - AVC. Так как с увеличением объема выпуска, Q, средние постоянные затраты уменьшаются, то, очевидно, что кривые АС и AVC сближаются с увеличением Q.
Слайд 16
Характер кривой средних переменных затрат
Средние переменные затраты (AVC)
принимают минимальное значение при объеме выпуска Q1.
Как
будут изменяться средние общие затраты (АTС) с дальнейшим увеличением выпуска?
Средние переменные затраты начинают возрастать, однако средние постоянные затраты (AFC) продолжают падать, вследствие чего средние общие затраты будут все-таки снижаться, пока снижение средних постоянных затрат не будет компенсировано ростом средних переменных затрат (на рисунке это произойдет при объеме выпуска Q2).
При дальнейшем увеличении объема выпуска средние общие затраты возрастают, несмотря на продолжающееся снижение средних переменных затрат.
Заметим, что Q2 > Q1, т.е., средние общие затраты, принимают свое минимальное значение при большем объеме выпуска, чем средние переменные затраты.
Слайд 17
Понятие предельных затрат
До сих пор мы имели дело с
величинами общих и средних затрат, однако часто встает необходимость
несколько иного подхода к понятию затрат.
Допустим, предприятие выпускает Q единиц продукции с общими затратами.
Возникает вопрос: на какую величину ΔТС увеличатся общие затраты при увеличении выпуска на ΔQ единиц. Такой подход приводит к понятию предельных затрат, т.е. приращению общих затрат, вызванному приращением объема производства на одну единицу.
МС = ΔТС/ ΔQ
Слайд 18
Общие предельные затраты
Если функция общих затрат дифференцируема, то
предельные затраты представляют собой первую производную функции общих затрат:
МС
= dTC/dQ = dTFC/dQ + dTVC/dQ = 0 + dTVC/dQ
Из формулы видно, что общие предельные затраты равны предельным переменным затратам и не зависят от постоянных затрат.
Это обстоятельство очевидно, так как общие постоянные затраты не изменяются с выпуском продукции, и изменение общих затрат равно изменению переменных затрат.
Слайд 19
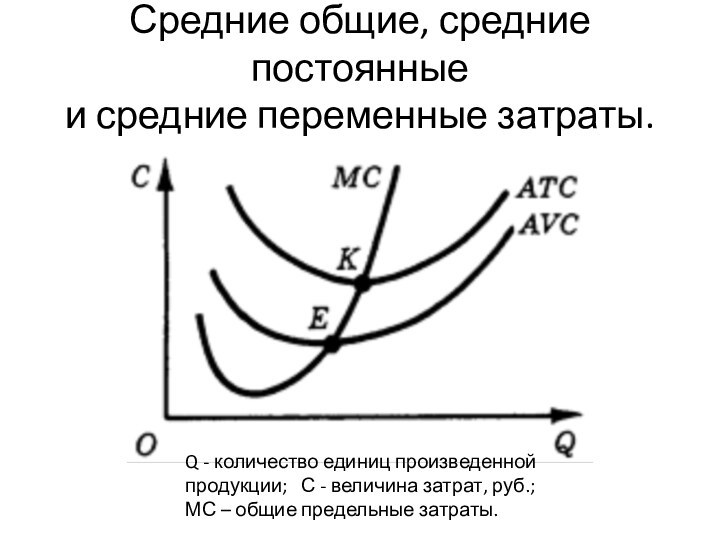
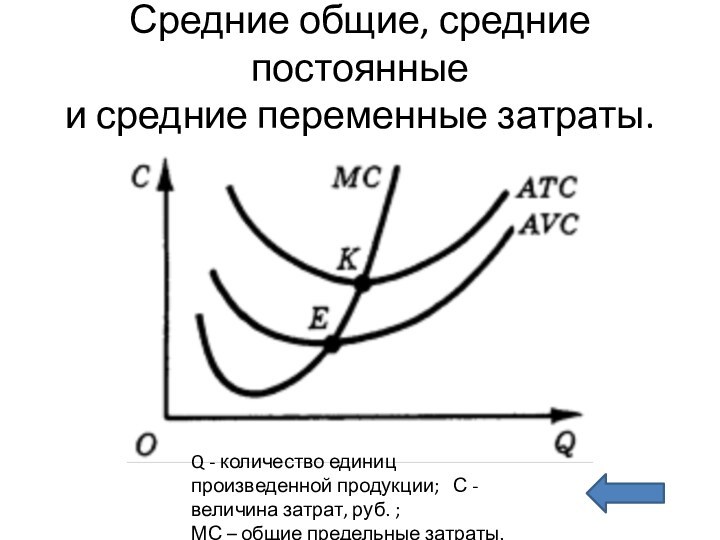
Средние общие, средние постоянные
и средние переменные затраты.
Q -
количество единиц произведенной продукции; С - величина затрат,
руб.;
МС – общие предельные затраты.
Слайд 20
Логическое объяснение связи функций предельных и средних затрат
Понятно,
что функции предельных и средних затрат весьма тесно взаимосвязаны.
Попробуем сначала объяснить эту связь логически.
Представим себе, что предельные затраты выше средних на каком-то интервале значений выпуска продукции.
Тогда приращение общих затрат, вызванное увеличением выпуска продукции на одну единицу, будет выше средних затрат на производство предыдущих единиц продукции.
Следовательно, средние затраты на этом интервале объемов выпуска возрастают.
Таким же образом можно показать, что в случае, если предельные затраты (приращение общих затрат при увеличении объема выпуска на одну единицу) ниже средних, средние затраты убывают.
Слайд 21
Строгое математическое доказательство связи функций предельных и средних
затрат
По определению
МС = dTC/dQ , АС = TC/Q
Отсюда
ТС =
АСQ, МС = dTC/dQ = dACQ/dQ
Следовательно,
MC = AC+QdAC/dQ
Из этого выражения можно сделать три вывода:
если АС возрастает, то dAC/dQ > 0.
Следовательно, МС > АС.
2) если АС убывает, то dAC < 0.
Следовательно, МС < АС.
3) в низшей точке кривой АС (при минимуме средних затрат) dAC/dQ = 0.
Следовательно, МС = АС.
Слайд 22
Вид кривой предельных затрат
Основываясь на этих рассуждениях и
исходя из графика функции средних общих затрат, построим график
функции предельных затрат совместно с графиком функции средних затрат.
Возрастающая ветвь кривой предельных затрат (МС) пересекает кривые средних переменных (AVC) и средних общих (ATС) затрат в точках их минимумов Е и K.
Проведенный в настоящем разделе анализ затрат пригодится при изучении поведения производителя в различных типах рыночных структур.
Слайд 23
Средние общие, средние постоянные
и средние переменные затраты.
Q -
количество единиц произведенной продукции; С - величина затрат,
руб. ;
МС – общие предельные затраты.