Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Лекция 5

Содержание

2. Дерево
3. Дерево
4. ДеревоКаждый узел дерева является корнем некоторого поддерева.Степень
5. Дерево
6. Деревья
7. Деревья
8. ДеревоЕсли существует путь из узла a в
9. Способы представления деревьевОриентированное дерево(oriented tree)Вложенные множества(nested sets)Вложенные скобкиСписок с отступами(indentation)
10. Способы представления деревьевa-b(c/d+e/f)
11. Порядок узловСыновья узла упорядочиваются слева направо. Следующие
12. Бинарные деревьяБинарное дерево – конечное множество узлов,
13. Представление деревьев в компьютереtypedef struct treeNode {
14. Представление деревьев в компьютере
15. Обход (traversing) дереваОбход дерева (проход по дереву)
16. Прямой порядок обхода1) Попасть в корень;2) Пройти левое поддерево;3) Пройти правое поддерево;АBDCEGFHJ
17. Внутренний порядок обхода1) Пройти левое поддерево;2) Попасть в корень;3) Пройти правое поддерево;DBAEGCHFJ
18. Обратный порядок обхода1) Пройти левое поддерево;2) Пройти правое дерево;3) Попасть в корень;DBGEHJFCA
19. Рекурсивный алгоритм прямого обходаподпрограмма preorder(дерево T) {
20. Рекурсивный алгоритм обратного обходаподпрограмма postorder(дерево T) {
21. Рекурсивный алгоритм внутреннего обходаподпрограмма inorder(дерево T) {
22. Скачать презентацию
23. Похожие презентации

Дерево

ДеревоКаждый узел дерева является корнем некоторого поддерева.Степень (degree) узла – количество поддеревьев

ДеревоЕсли существует путь из узла a в узел b, тогда a называется

Способы представления деревьевОриентированное дерево(oriented tree)Вложенные множества(nested sets)Вложенные скобкиСписок с отступами(indentation)

Способы представления деревьевa-b(c/d+e/f)

Порядок узловСыновья узла упорядочиваются слева направо. Следующие два дерева различны, так как

Бинарные деревьяБинарное дерево – конечное множество узлов, которое является пустым или состоит

Представление деревьев в компьютереtypedef struct treeNode { int info; struct

Обход (traversing) дереваОбход дерева (проход по дереву) – метод исследования дерева, когда

Прямой порядок обхода1) Попасть в корень;2) Пройти левое поддерево;3) Пройти правое поддерево;АBDCEGFHJ

Внутренний порядок обхода1) Пройти левое поддерево;2) Попасть в корень;3) Пройти правое поддерево;DBAEGCHFJ

Обратный порядок обхода1) Пройти левое поддерево;2) Пройти правое дерево;3) Попасть в корень;DBGEHJFCA

Рекурсивный алгоритм прямого обходаподпрограмма preorder(дерево T) { если T != NULL

Рекурсивный алгоритм обратного обходаподпрограмма postorder(дерево T) { если T != NULL

Рекурсивный алгоритм внутреннего обходаподпрограмма inorder(дерево T) { если T != NULL

Дерево как АТДК деревьям как к АТД применяются следующие операторы:parent(n, t) –

Слайды презентации

Слайд 2 Дерево

Слайд 3 Дерево

Слайд 4 Дерево
Каждый узел дерева является корнем некоторого поддерева.
Степень (degree)

ДеревоКаждый узел дерева является корнем некоторого поддерева.Степень (degree) узла – количество

узла – количество поддеревьев узла.
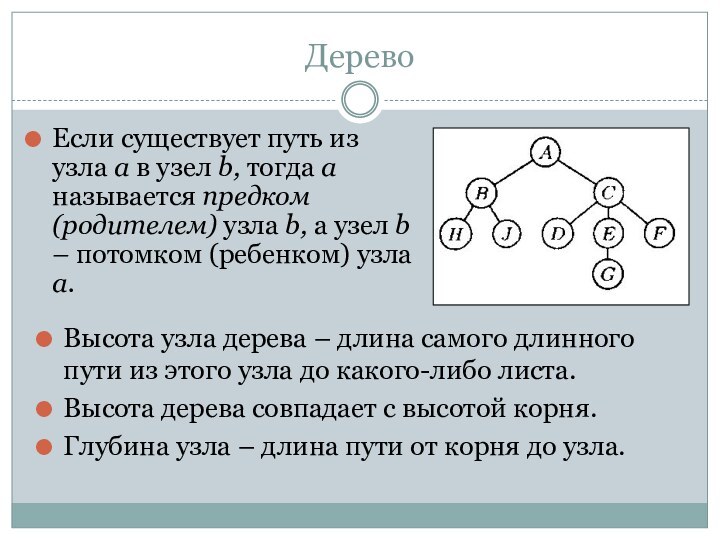
Концевой узел (terminal node) или

лист (leaf) – узел со степенью 0.
Узел ветвления (branch node) – неконцевой узел.
Уровень (level) узла по отношению к дереву Т: уровень корня дерева Т равен 0, а уровень любого другого узла на 1 выше, чем уровень корня ближайшего поддерева Т, содержащего данный узел.

Слайд 5 Дерево

Слайд 6 Деревья

Слайд 7 Деревья

Слайд 8 Дерево
Если существует путь из узла a в узел

ДеревоЕсли существует путь из узла a в узел b, тогда a

b, тогда a называется предком (родителем) узла b, а

узел b – потомком (ребенком) узла a.

Высота узла дерева – длина самого длинного пути из этого узла до какого-либо листа.
Высота дерева совпадает с высотой корня.
Глубина узла – длина пути от корня до узла.

Слайд 9 Способы представления деревьев
Ориентированное дерево
(oriented tree)
Вложенные множества
(nested sets)
Вложенные скобки
Список

с отступами
(indentation)

Слайд 10 Способы представления деревьев
a-b(c/d+e/f)

Слайд 11 Порядок узлов
Сыновья узла упорядочиваются слева направо. Следующие два

Порядок узловСыновья узла упорядочиваются слева направо. Следующие два дерева различны, так

дерева различны, так как порядок сыновей узла a различен.

Неупорядоченное

дерево – дерево, в котором порядок сыновей игнорируется. Иначе дерево называется упорядоченным.

Слайд 12 Бинарные деревья
Бинарное дерево – конечное множество узлов, которое

Бинарные деревьяБинарное дерево – конечное множество узлов, которое является пустым или

является пустым или состоит из корня и двух непересекающихся

бинарных деревьев, которые называются левым и правым поддеревьями данного дерева.
Остальные деревья называют сильноветвящимися.

Слайд 13 Представление деревьев в компьютере
typedef struct treeNode {

Представление деревьев в компьютереtypedef struct treeNode { int info; struct treeNode

int info;
struct treeNode llink, rlink;
} treeNode;

treeNode *t

– переменная связи, указатель на дерево.
llink – указатель на левое поддерево;
rlink – указатель на правое поддерево.

Слайд 14 Представление деревьев в компьютере

Слайд 15 Обход (traversing) дерева
Обход дерева (проход по дереву) –

Обход (traversing) дереваОбход дерева (проход по дереву) – метод исследования дерева,

метод исследования дерева, когда каждый узел посещается в точности

один раз.
Три способа обхода:
в прямом порядке (preorder);
в обратном порядке (postorder);
во внутреннем (центрированном) порядке, симметричный обход (inorder);