Слайд 2
ОБУЧЕНИЕ НУМЕРАЦИИ В ПРЕДЕЛАХ 1000
Знакомство с устной нумерацией
в пределах 1000 начинается с повторения:
счета единицами до
10;
замены 10 единиц одним десятком;
счета десятками до 100;
замены 10 десятков одной сотней.
Слайд 4
Счет сотнями связывается с раздроблением рублей и метров
соответственно в копейки и сантиметры. Рассуждение проводится так: «1
р. — 100 к., значит, в 2 р. содержится 200 к., в 5 р. 500 к. и т. д.».
Слайд 5
Получение полных трехзначных чисел из сотен, десятков, единиц.
Учитель
просит взять 1 сотню палочек, 2 десятка палочек и
прибавить еще 3 палочки — получилось число сто двадцать три. Это число учащиеся должны отложить на счетах, на пособиях из арифметического ящика.
Слайд 6
Получение трехзначных чисел из сотен и десятков, сотен
и единиц.
Учитель берет одну сотню палочек. «Сколько это палочек?»
— спрашивает учитель. Прибавили три десятка палочек или тридцать: «Какое число получили из 1 сотни и 3 десятков?» «Сто тридцать», — отвечают ученики
Учитель объясняет, почему в числе пишется нуль.
Слайд 7
Можно дать и обратное задание: разложить числа 935
на разрядные числа. Учащиеся раскладывают в строчку 935 [900]
[30| [5]
Полезно задание: назвать и записать число, которое состоит из 5 сот. 6 дес. 3 ед., 5 сот. 3 ед., 5 сот. 6 дес.
Слайд 8
Счет единицами
Учитель предлагает взять одну сотню палочек (кубиков)
и считать к ней еще одну палочку, получили сто
один, прибавить еще одну палочку, получим сто два и т. д.
Особое внимание обращается на переход к новой сотне, новому десятку: 299, 300; 439, 440, что всегда затрудняет учащихся.
Слайд 9
Работа проводится и на счетах. Это позволяет отработать
переход к новому десятку, к новой сотне, размен десятков
и сотен. Важно, чтобы учащиеся и на примерах могли показать образование последующего или предыдущего числа в числовом ряду путем прибавления или вычитания единицы:
199+1=200 500-1=499
345+1=346 348-1=347
999+1 = 1000 1000-1= 999
Слайд 11
Весьма важным при изучении нумерации является различение учащимися
количества разрядных единиц в числе и общего количества единиц.
Учащиеся должны понимать, что на первом месте справа стоят единицы, на втором — десятки, на третьем — сотни и т. д., и уметь отвечать на такие вопросы: «Покажи и назови, сколько единиц в числе, сколько десятков в числе. Покажи, где стоят в числе 348 десятки, единицы. Назови, сколько их».
Слайд 12
Определение единиц в числе
Учитель просит школьников поставить три
точки и над числом 325. Особенно такой прием помогает
учащимся при записи числа с нулями в середине или в конце (507, 460), как известно, умственно отсталые школьники при записи таких чисел пропускают нули, вписывают лишние или переставляют. Например, вместо 507 записывают: 5007, 570.
Слайд 13
СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 1000
Сложение и вычитание
круглых сотен:
200 + 100 =
2 сот. + 1 сот.=3
сот.=300
500 - 200=
5 сот.-2 сот.=3 сот.=300
Слайд 14
Сложение и вычитание круглых сотен и единиц, круглых
сотен и десятков (действия основываются на знании нумерации):
а) 300+
5 305- 5 5+300 305-300
б) 300+ 40 340- 40 40+300 340-300
в) 300+ 45 345- 45 45+300
Слайд 15
Сложение и вычитание круглых десятков, а также круглых
сотен и десятков:
430+20=
рассуждения проводятся так: «430 — это 4
сот. и 3 дес., 20 — это 2 дес. Складываем десятки: 3 дес.+2 дес. = 5 дес. 4 сот.+5 дес.=450».
Слайд 16
Особые случаи сложения и вычитания
308+121
308+100=408
408+ 20=428
428+ 1=429
Слайд 17
Проверка
Часто при выполнении проверки ученик получает несоответствие между
полученным результатом и заданным примером, но это не служит
ему поводом для исправления неверного ответа, например: 570-150=320.
Проверка. 320+150=470.
Слайд 18
Сложение и вычитание с переходом через разряд.
Ошибки:
_375
6
975
Особенно трудны случаи, при решении которых:
переход
через разряд происходит в двух разрядах;
получается нуль в одном из разрядов;
содержится нуль в уменьшаемом;
в середине уменьшаемого стоит единица.
Слайд 19
Учитывая трудности изучения данной темы, необходимо повторить с
учащимися сложение и вычитание с переходом через разряд в
пределах 20 и 100, обратить внимание на решение примеров, в которых компонентом является нуль, или нуль получается в одном из разрядов суммы или разности (17+3, 25+15, 36-6, 36—27), или нуль содержится в одном из разрядов уменьшаемого или вычитаемого (60—45, 75—40).
Слайд 20
При объяснении решения примеров с переходом через разряд,
учитывая, что умственно отсталые школьники при сложении забывают прибавлять
то число, которое надо запомнить, можно разрешать надписывать это число над соответствующим разрядом.
Слайд 21
Следует сопоставить сначала 1-й и 2-й, а потом
2-й и 3-й примеры, особенности их решения, объяснить, в
чем их различие, почему получаются разные ответы
Слайд 22
Умножение и деление
в пределах 1000
Полезно сопоставим, умножение и
деление единиц, десятков и сотен:
3х3= 9 8:4= 2
30х3= 90 80:4= 20
300х3=900 800:4=200
Слайд 23
При объяснении проводятся следующие рассуждения:
«60х3=?
60 —
это 6 десятков
6 дес.х3=18 дес.
18 десятков —
это 180, значит, 60х3=180».
Слайд 24
Успех выполнения действий здесь зависит от умения учащихся
раскладывать числа на разрядные слагаемые
123х3=?
123 = 100+20+3
100х3=300
20х3=
60
3х3= 9
300+60+9=369
Слайд 26
Умножение трехзначных чисел с нулем на конце или
в середине не требует особо пристального внимания, так как
учащихся не затрудняет умножение нуля: они путают его со сложением с нулем. Поэтому предварительно надо повторить умножение нуля и нуль (0x3, 5x0).
Слайд 27
Запись умножения двузначного числа на двузначное число надо
объяснить подробно, показав аналогию с записью чисел в столбик
при сложении и вычитании (единицы и десятки множителей подписываются соответственно друг под другом, и умножение начинается с единиц).
Слайд 29
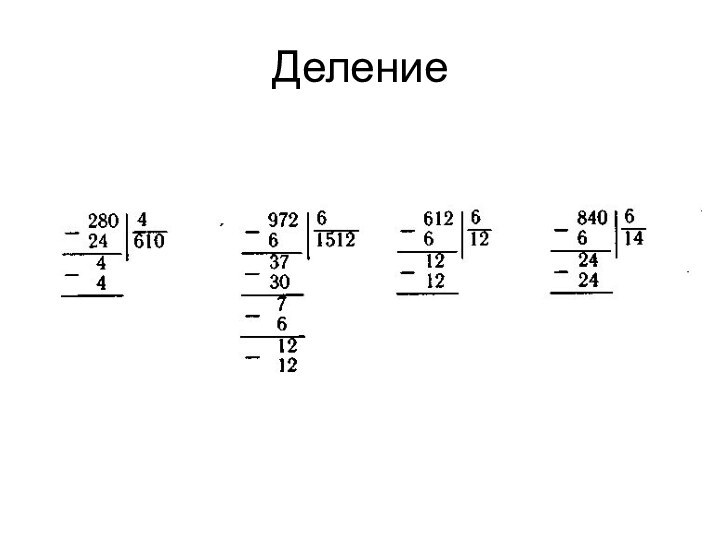
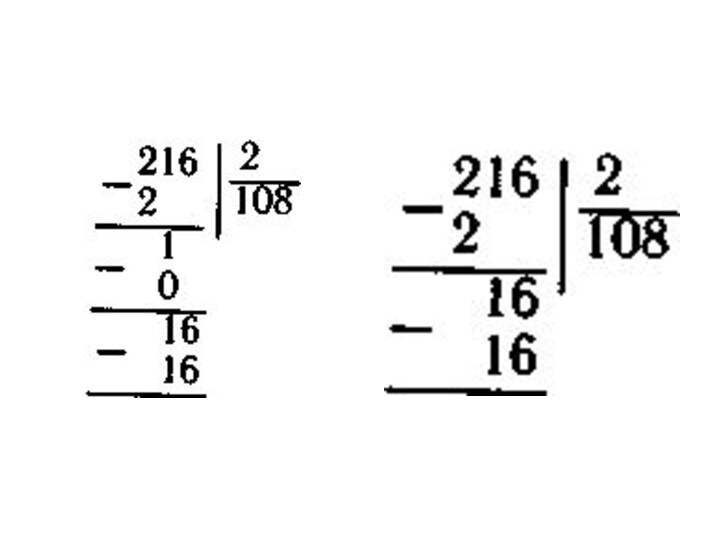
Для того чтобы предотвратить ошибки в вычислениях необходимо
задолго до знакомства с приемами письменного деления провести подготовительную
работу:
Постоянно, на каждом уроке повторять таблицу умножения и деления.
Решать примеры на деление с остатком: 15:2=7 (ост. 1);
21:4=5 (ост. 1); 82:2= 40 (ост. 2)и т. д., обращая внимание на то, что остаток должен быть всегда меньше делителя. Подбор цифр частного, например 24:5, следует производить постепенно:
24 на 5 не делится, делим 23, потом 22, 21, наконец, 20.
С самого начала знакомства с делением в столбик надо учить детей прикидке ответа, умению сразу определять, сколько цифр должно получиться в ответе.
Слайд 31
Деление на круглые десятки
Учащиеся убеждаются, что если делимое
и делитель оканчиваются нулями, то частное легче получить, если
деление выполнять, не обращая внимания на нули, т. е. мысленно отбросить (120:20=6). При этом обращается внимание учащихся на то, что, отбрасывая нуль в делимом, мы его делим на 10.