- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Модель ионной имплантации
Содержание
- 2. Профиль распределения ионно-импантированной примеси в Si или
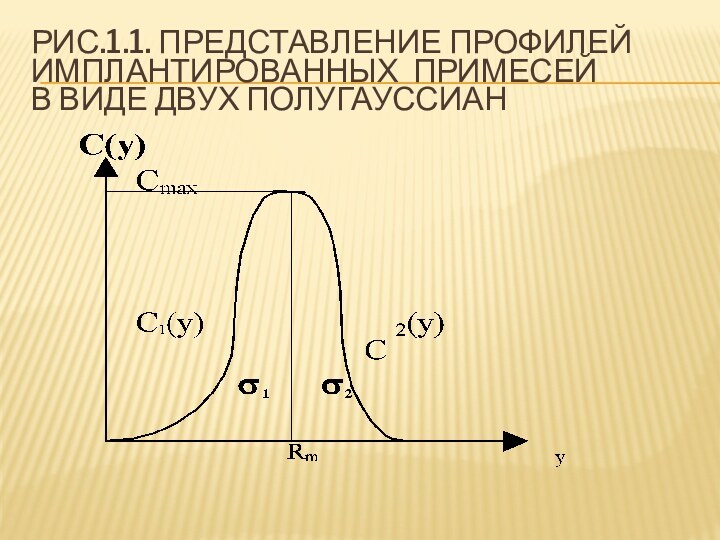
- 3. Рис.1.1. Представление профилей имплантированных примесей в виде двух полугауссиан
- 4. Для сшивки распределения в виде двух
- 5. В программе SUPREM II значения Rm, 1
- 6. Модальный Rm и проективный Rp пробеги, стандартное
- 8. Максимальное значение концентрации Сy и доза Q связаны соотношением
- 9. При имплантации через SiO2 следует использовать оба
- 10. R|mSi = RmSi
- 11. Профиль имплантированного бора.В работе [23] показано, что
- 12. В программе SUPREM II распределение PEARSON IV
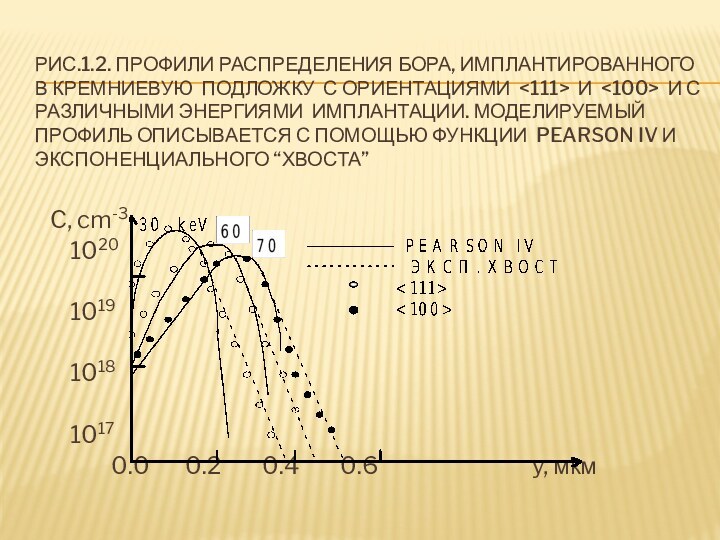
- 13. Рис.1.2. Профили
- 14. Стандартное распределение PEARSON IV вычисляется следующим образом
- 15. Константа C0 определяется из нормировки на дозу имплантации
- 16. Скачать презентацию
- 17. Похожие презентации
Профиль распределения ионно-импантированной примеси в Si или SiO2 можно представить в виде симметричной гауссианы с двумя моментами: проективным пробегом, Rp , и стандартным отклонением, p, вычисляемыми из теории Линдхарда-Шарфа-Шиотта (ЛШШ) [20]. Это простейший способ. Однако экспериментальные









![Модель ионной имплантации Профиль имплантированного бора.В работе [23] показано, что профиль имплантированного бора может быть](/img/tmb/14/1308151/0092fa48721675c83f33680cc3482c50-720x.jpg)




Слайд 4 Для сшивки распределения в виде двух полугауссиан обе
кривые определяются выражениями:
C1 (y)= Cmax exp [-(y-Rm)2 /2σ 12]
0 y Rm; C2 (y)= Cmax exp [-(y-Rm)2 /2σ 22] Rm y .
Слайд 5 В программе SUPREM II значения Rm, 1 и
2 получаются из алгоритма, описанного в работе [22], в
котором используются Rp, p и третий момент, Sk (skewness – скошенность) – параметр, характеризующий асимметрию профиля. Эти три величины получаются путем интерполяции табличных параметров имплантации примесей в Si или SiO2 [22].Слайд 6 Модальный Rm и проективный Rp пробеги, стандартное отклонение
s и среднеквадратичный пробег (страгглинг) связаны посредством соотношений
Rm= RP
+ 0.8(∆Rp1 - ∆Rp2); ∆Rp = σ; σ2= Слайд 7 Для построения профиля распределения концентрации ионно-имплантиро-ванной примеси, кроме
энергии имплантации, следует задать и дозу. Нормализованная доза имплантации
определяется из выраженияСлайд 9 При имплантации через SiO2 следует использовать оба значения
1 и 2 и Rm для обеих (SiO2 -
Si) областей концентрационного профиля. Поскольку энергетические потери в SiO2 ненамного отличаются от потерь в Si, модальный пробег в Si изменяется с целью учета этой разницы посредством аппроксимации:Слайд 10 R|mSi = RmSi +
(1-RPsi /RPox)Zox
где Zox - толщина SiO2 ;
R/mSi и RmSi
- исправленные и неисправленные значения модального пробега в Si;RpSi и Rpox - проективные пробеги в Si и SiO2 соответственно.
Небольшой разрыв в профиле на разделе SiO2 / Si получается вследствие использования такого приближения.
Слайд 11
Профиль имплантированного бора.
В работе [23] показано, что профиль
имплантированного бора может быть описан с помощью распределения PEARSON
IV. В этой работе экспериментально определен и четвертый момент 2. Несмотря на то, что такое приближение хорошо описывает профиль распределения бора от поверхности до расстояния, немного ниже максимума концентрации, экспериментальный профиль отличается от модельного “хвостом”, обусловленным рассеянием ионов бора вдоль направления каналирования (рис.1.2).Слайд 12 В программе SUPREM II распределение PEARSON IV для
имплантационного профиля бора на основе экспериментальных данных [24-26] модифицировано
посредством добавлением экспоненциального хвоста с фиксированной характеристической длиной (0.45 мкм), независимой от энергии, дозы и кристаллографической ориентации поверхности. Хвост сшивается со стандартным распределением PEARSON IV в том месте, где концентрация бора падает на 50% от ее значения в максимуме. Очевидно, после добавления хвоста следует произвести перенормировку распределения на дозу имплантируемых ионов. Типичные результирующие профили для такой модификации показаны на рис.1.2.Слайд 13 Рис.1.2. Профили распределения бора, имплантированного в кремниевую
подложку с ориентациями и и с различными
энергиями имплантации. Моделируемый профиль описывается с помощью функции PEARSON IV и экспоненциального “хвоста”
C, cm-3
1020
1019
1018
1017
0.0 0.2 0.4 0.6 y, мкм





























