Слайд 2
Пояснительная записка
Предлагаемый курс является предметно-ориентированным.
Цель: научить решать
задачи на оптимизацию с помощью нахождения производной функции
Задачи:
1) Подготовить
учащихся к осознанному выбору сферы деятельности;
2) Развить интерес школьников к предмету;
3) Показать связь математических методов с логистикой;
4) Помочь учащимся отойти от математических штампов; расширить их математический и общенаучный кругозор.
Слайд 3
Новизна, актуальность, педагогическая целесообразность.
Данная тема не рассматривается подробно
в школьном курсе математике. Школьники не имеют возможности подробно
познакомиться с практическим применением производной, с методами решения задач на оптимальное распределение ресурсов. В ходе ознакомления с этой темой, школьники имеют возможность закрепить свои знания по теме функции, производные функций, нахождение наибольшего и наименьшего значения функции и прочих тем, связанных с изучаемой.
Слайд 4
Форма и режим занятий
Занятия будут проходить по одному
уроку раз в неделю, в четвертой четверти.
Проведение курса
должно совпасть с изучением темы производной на основных уроках.
Используются различные формы уроков: лекция, урок
Слайд 5
Ожидаемые результаты
Школьники должны закрепить знания по теме производная
функций. Должны научиться решать задачи на оптимизацию с помощью
производной функции.
Слайд 6
Способы проверки
Оценки будут выставляться за работу на занятиях
(ответы на вопросы, решения задач у доски).
Итоговая аттестацию будет
проходить с ориентировкой на оценки полученные в ходе все курса.
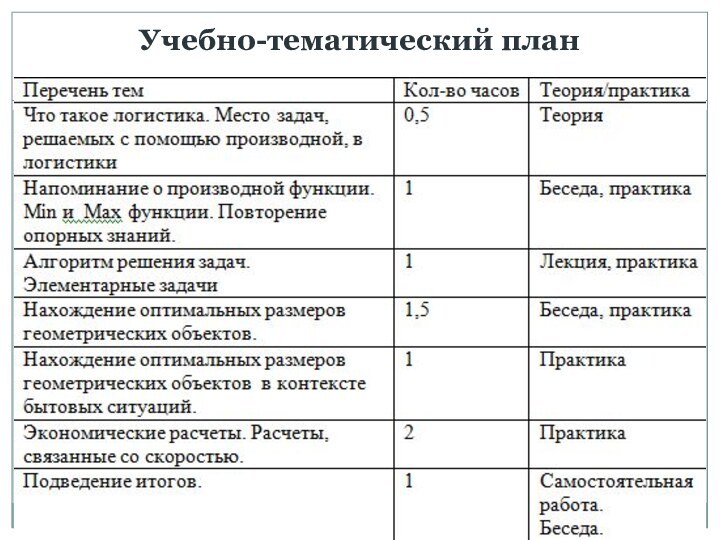
Слайд 8
Что такое логистика. Место задач, решаемых с помощью
производной, в логистики
Учитель рассказывает о профессии логиста, об основных
задачах этой профессии, о проблемах с которыми сталкивается логист и как их решать с помощью производной.
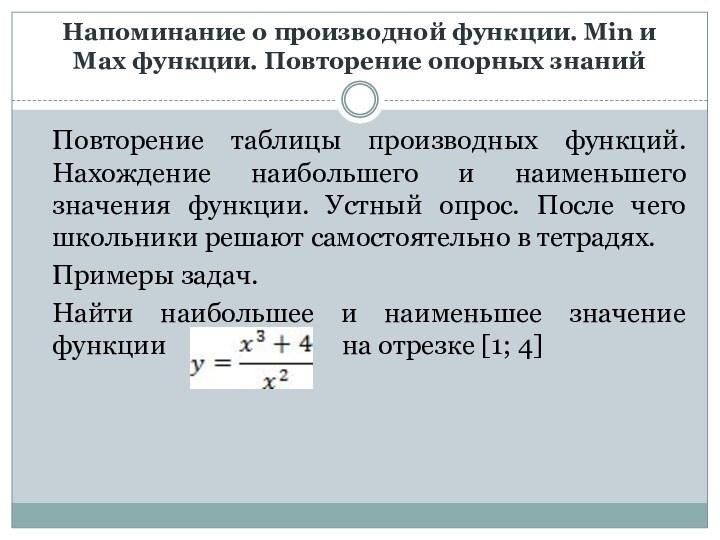
Слайд 9
Напоминание о производной функции. Min и Max функции.
Повторение опорных знаний
Повторение таблицы производных функций. Нахождение наибольшего и
наименьшего значения функции. Устный опрос. После чего школьники решают самостоятельно в тетрадях.
Примеры задач.
Найти наибольшее и наименьшее значение функции на отрезке [1; 4]
Слайд 10
Алгоритм решения задач.
Элементарные задачи.
Говорит об этапах решении задач
и о том, как их реализовывать.
Составление математической модели.
Работа
с составленной моделью
Ответ на вопрос
Пример задачи
Найти оптимальные размеры сторон прямоугольника, что бы его площадь была наибольшей, если его периметр равен 30.
Слайд 11
Нахождение оптимальных размеров геометрических объектов
Несколько задач разбираются у
доски, остальные решаются в тетради.
Пример задачи.
Коническая воронка, с образующей
равной 20 см. Какова должна быть Высота воронки, что бы ее объем был наибольшим?
Слайд 12
Экономические расчеты. Расчеты, связанные со скоростью
Несколько задач разбираются
у доски, остальные решаются в тетради.
Пример задачи.
Буровая вышка расположена
в поле в 9км от ближайшей
точки шоссе. С буровой надо направить курьера в населенный
пункт, расположенный по шоссе в 15км от упомянутой точки.
Скорость курьера на велосипеде по полю 8км/ч, а по шоссе 10км/ч.
К какой точке шоссе ему надо ехать, чтобы в кратчайшее время
достичь населенного пункта?
Слайд 13
Подведение итогов
В начале урока школьники тянут билеты и
решают в тетради самостоятельно по одной задачи. После решения
проходит обсуждение затруднений.Выставляются итоговые отметки.
Слайд 14
Литература
Алгебра и начала математического анализа. 10—11 классы. В
2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений
(базовый уровень) / [А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Г. Мишустина, П. В. Семенов, Е. Е. Тульчинская ] ; под ред. А. Г. Мордковича.
Вулих Б.З. Введение в функциональный анализ (2-е изд.). М.: Наука, 1967
Бермант А.Ф. Курс математического анализа. Часть I (12-е изд.). М. Физматгиз, 1959