Презентация на тему Обработка результатов

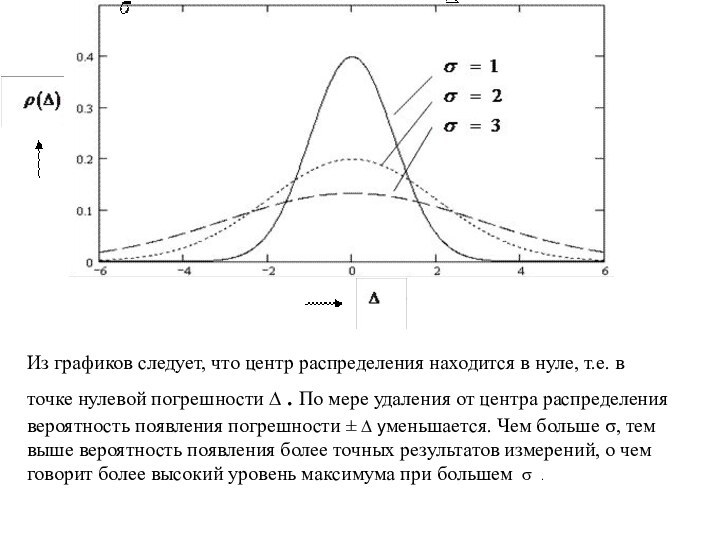
точности вполне достаточно
Результат однократного измерения представляется в следующем виде:
Qi

= Yi + Δi,
где Yi - значение i - го показания;Δi - поправка.
Погрешность результата однократного измерения определяется при утверждении метода проведения измерений.

закона распределения
нормальный закон распределения
равномерный закон распределения
корреляционный закон распределения

(теоремой Ляпунова), согласно которой распределение случайных погрешностей будет близко

к нормальному во всех случаях, когда результаты наблюдений формируются под влиянием большого числа независимых факторов, каждый из которых оказывает незначительное действие по сравнению с суммарным действием остальных.

непрерывный ряд значений от - ᴔдо + ᴔ  ;
равные

по абсолютному значению погрешности +∆ и  -∆ равновероятны;
малые по абсолютному значению погрешности более вероятны, чем большие.

погрешности ∆ 

нуле, т.е. в точке нулевой погрешности ∆ . По

мере удаления от центра распределения вероятность появления погрешности ± ∆ уменьшается. Чем больше σ, тем выше вероятность появления более точных результатов измерений, о чем говорит более высокий уровень максимума при большем  σ .

параметры распределения
Математическое ожидание распределение Хц=(х1+х2)/2.
Среднее квадратическое отклонение в зависимости

от распределения определяется по формуле: 

посредством которых непосредственно получается значение измеряемой величины. Равноточными или равнорассеянными

называют прямые, взаимно независимые измерения определенной величины, причем результаты этих измерений могут быть рассмотрены как случайные и распределенные по одному закону распределения. Обычно при обработке результатов прямых равноточных измерений предполагается, что результаты и погрешности измерений распределены по нормальному закону распределения.

формуле
где xi — значение измеряемой величины; n — количество проведенных

измерений. если систематическая погрешность определена, ее значение вычитают из вычисленного значения математического ожидания. Потом вычисляется значение среднеквадратического отклонения значений измеряемой величины от математического ожидания.

рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей).

Промах — это результат xп отдельного наблюдения, входящего в ряд из  n  наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.

отдельные результаты нельзя, так как это может привести к

фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое Х результатов наблюдений  хi по формуле

Затем вычисляют оценку Среднее квадратическое отклонение результата наблюдения. Находят отклонение vп  предполагаемого промаха xп от  :

http://metrologe.ru/otvety-k-ekzamenu-metrologiya/439-obrabotka-rezultatov-serij-izmerenij-algoritm.html

погрешность, то ее необходимо исключить из результатов измерений. Вычислить математическое

ожидание результатов измерений. В качестве математического ожидания обычно берется среднее арифметическое значений. Установить величину случайной погрешности (отклонения от среднего арифметического) результата однократного измерения. Вычислить дисперсию случайной погрешности. Вычислить среднеквадратическое отклонение результата измерения. Проверить предположение, что результаты измерений распределены по нормальному закону. Найти значение доверительного интервала и доверительной погрешности. Определить значение энтропийной погрешности и энтропийного коэффициента.