Презентация на тему Основы теории вероятности

наступления некоторого события.
А - случайное событие – вероятность данного события

обозначается через Р(А).
для любого события А: 0 < Р(А) < 1.

ω2, ω3, ω4, ω5, ω6}, - Случайные события (события),

будем называть подмножества пространства элементарных событий Ω.

={ω}. Элементы ω этого множества Ω называют элементарными событиями.

невозможным событием
противоположным (отрицанием события А) событию A называется событие,

состоящее в том, что событие A не произошло. Обозначается Ā, Ā= Ω\А
несовместными событиями называются события A и B, для которых A B = Ø.

событие С, которое состоит в том, что происходит хотя

бы одно из событий А и В. С = A  В или С = А + В.
пересечением, или произведением событий А и В называют событие С, которое состоит в том, что происходят оба события А и В. С = А  В или С = АВ
Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.

А.
Р(А + В) = Р(А) + Р(В), если события

А и В несовместимы, а в общем случае Р(А + В) = Р(А) + Р(В) - Р(АВ).
Вероятность достоверного события равна 1, а невозможного события — нулю.

Р(АВ) = Р(А)Р(В).

события В, вычисленную в предположении, что событие А уже

наступило.
Р(АВ) = Р(В)Р(А|В)= Р(А)Р(В|А)

распределение вероятностей Рξ на X

F{x) = Р(ξ ≤ х).

t (иногда — плотностью случайной величины ξ), если (для

любых чисел а,b (пусть а < b)

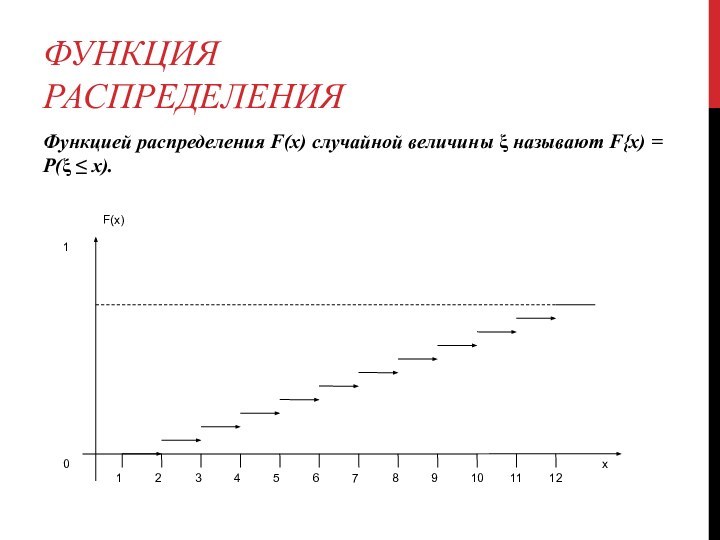
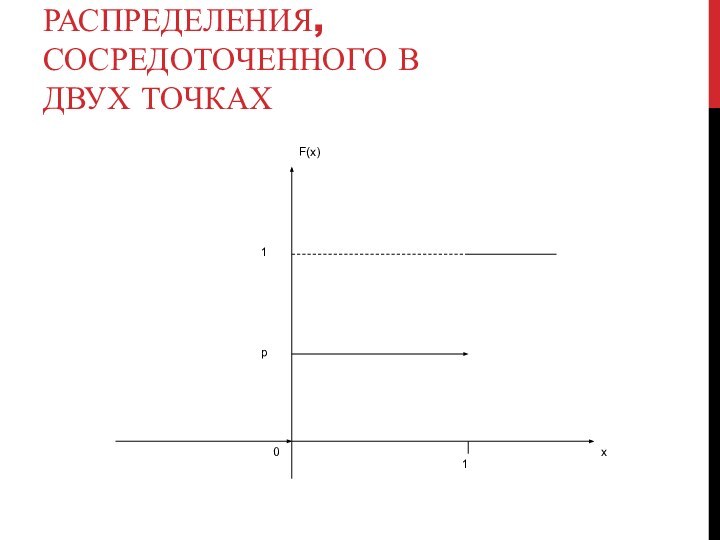
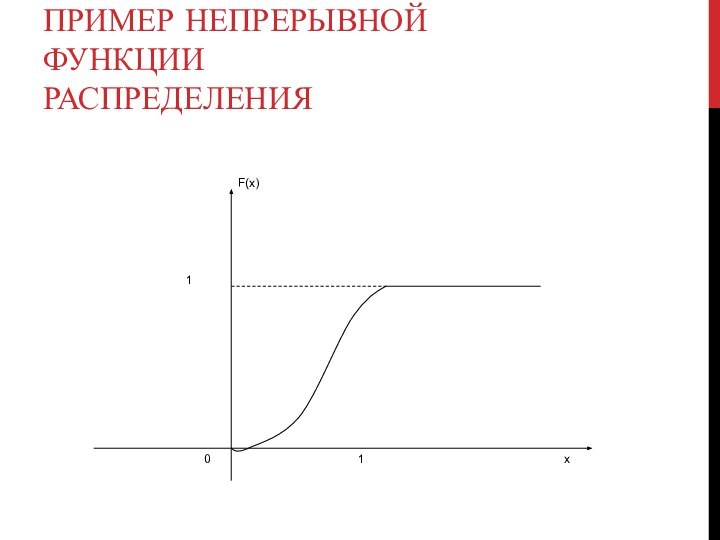
Р(а < ξ < b) =