- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Оценка достоверности результатов статистического исследования
Содержание
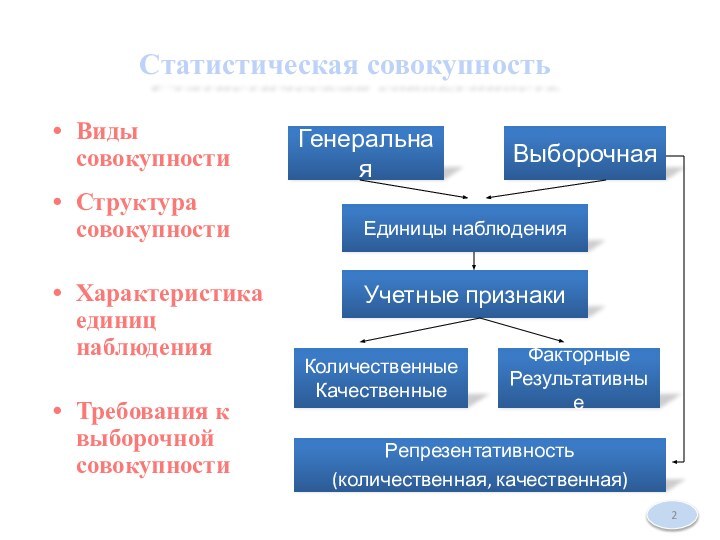
- 2. Статистическая совокупностьВиды совокупностиСтруктура совокупностиХарактеристика единиц наблюденияТребования к выборочной совокупностиГенеральнаяВыборочнаяЕдиницы наблюденияУчетные признакиКоличественныеКачественныеФакторныеРезультативныеРепрезентативность (количественная, качественная)
- 3. Виды совокупностиГенеральная – группа, состоящая из всех
- 4. Требования , предъявляемые к выборочной совокупности –
- 5. Виды наблюдения:Текущее наблюдение – регистрация проводится постоянно,
- 6. Сплошное наблюдение – регистрация всех единиц наблюдения,
- 7. Методы отбора изучаемых явлений и формирования выборочной
- 8. Методы отбора изучаемых явлений и формирования выборочной
- 9. 1. Оценка достоверности результатов статистического исследования путем
- 10. Средняя ошибка средней арифметической величины (m)
- 11. Методика расчета
- 12. 2. Определение доверительных границ средних и относительных
- 13. Для медико-биологических исследований считается достаточной степень вероятности
- 14. Результаты измерения длины тела при рождении у
- 15. Рассчитать среднюю ошибку коэффициента и определить доверительные
- 16. 3. Оценка достоверности разности результатов исследования применяется когда
- 17. Формулы определения достоверности разностиЕсли критерий t≥2,
- 18. Задача на оценку достоверности разности средних величин Необходимо
- 19. Скачать презентацию
- 20. Похожие презентации
















Слайд 2
Статистическая совокупность
Виды совокупности
Структура совокупности
Характеристика единиц наблюдения
Требования к выборочной
совокупности
Слайд 3
Виды совокупности
Генеральная – группа, состоящая из всех относительно
однородных элементов, в соответствии с поставленной целью
Выборочная – отобранная
для исследования часть генеральной совокупности и предназначенная для характеристики всей генеральной совокупностиСлайд 4 Требования , предъявляемые к выборочной совокупности – репрезентативность
(представительность, достоверность)
Количественная репрезентативность – достаточная численность элементов выборочной совокупности
(рассчитывается по таблицам и формулам)Качественная репрезентативность – соответствие признаков, характеризующих элементы выборочной совокупности по отношению к генеральной
Слайд 5
Виды наблюдения:
Текущее наблюдение – регистрация проводится постоянно, по
мере возникновения единиц наблюдения
Единовременное наблюдение – сбор информации по
каждой единице наблюдения изучаемого явления приурочен к какому либо определенному моментуСлайд 6 Сплошное наблюдение – регистрация всех единиц наблюдения, составляющих
генеральную совокупность
Выборочное (несплошное наблюдение) – изучение части совокупности для
характеристики генеральной совокупности
Слайд 7
Методы отбора изучаемых явлений и формирования выборочной совокупности
Случайный
отбор – проводится по жребию (по начальной букве фамилии,
по дню рождения и т.п.)Механический отбор – из всей совокупности берется для изучения механически отобранная единица наблюдения (каждая десятая и т.д.)
Гнездовой серийный отбор – выбираются не отдельные единицы, а гнезда (серии), которые отбираются путем случайной или механической выборки
Слайд 8
Методы отбора изучаемых явлений и формирования выборочной совокупности
Метод
основного массива применяется при изучении тех объектов, в которых
сосредоточено большинство изучаемых явленийСлайд 9 1. Оценка достоверности результатов статистического исследования путем определения
ошибок репрезентативности
При проведении выборочных исследований полученный результат не обязательно
совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности (средняя ошибка средней или относительной величины).
Слайд 10
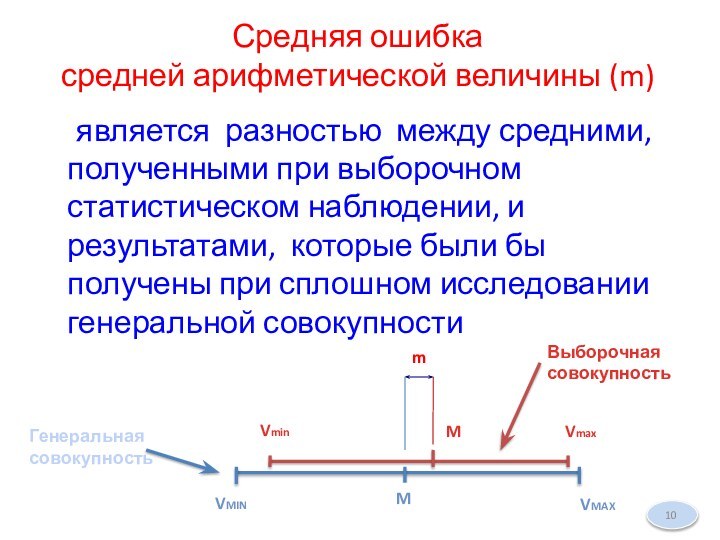
Средняя ошибка
средней арифметической величины (m)
является разностью между
средними, полученными при выборочном статистическом наблюдении, и результатами, которые
были бы получены при сплошном исследовании генеральной совокупностиVmin
Vmax
M
Генеральная совокупность
Vmin
Vmax
M
Выборочная совокупность
m
Слайд 12
2. Определение доверительных границ средних и относительных величин
При
n>30,степени вероятности безошибочного прогноза P=99.7% соответствует значение t=3, при
P=95.5% - значение t=2Применяется в случаях, когда по результатам исследования выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности
При n≤30, величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице (Н.А.Плохинского)
Слайд 13 Для медико-биологических исследований считается достаточной степень вероятности безошибочного
прогноза, равная 95%, при этом число случаев генеральной совокупности,
в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%.При ряде исследований, связанных, например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей, установленных в выборочной совокупности.
t = 2
t = 3
Слайд 14 Результаты измерения длины тела при рождении у 45
девочек (в см): 48, 54, 53, 49, 51, 53,
51, 48, 52, 51, 53, 49, 50, 53, 48, 52, 50, 52, 50, 52, 50, 51, 52, 53, 47, 52, 48, 48, 52, 50, 46, 46, 54, 55, 56, 48, 52, 52, 51, 53, 53, 48, 50,54,48.Вычислите ошибку средней арифметической величины и доверительный интервал при степени вероятности безошибочного прогноза 95,5%
Слайд 15 Рассчитать среднюю ошибку коэффициента и определить доверительные границы
с вероятностью достоверного прогноза на 95%, если на предприятии
среднегодовое число рабочих составило 400 человек, из них в течение года болело 240Определить среднюю ошибку показателя и доверительные границы с вероятностью безошибочного прогноза 95%, если известно, что при наблюдении 400 больных отдельным заболеванием частота осложнений составила 20%
Слайд 16
3. Оценка достоверности разности результатов исследования
применяется когда необходимо
определить, случайны или достоверны (существенны) различия между двумя средними
величинами или относительными показателями, т.е. обусловлены ли эти различия каким-либо фактором или они случайны
Слайд 17
Формулы определения
достоверности разности
Если критерий t≥2, что соответствует
вероятности безошибочного прогноза
P ≥ 95.5 %, то разность
следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности Если критерий t<2, вероятность безошибочного прогноза
P < 95.5 %. Это означает, что разность недостоверна (несущественна, случайна), т.е. не обусловлена какой-то закономерностью
Слайд 18
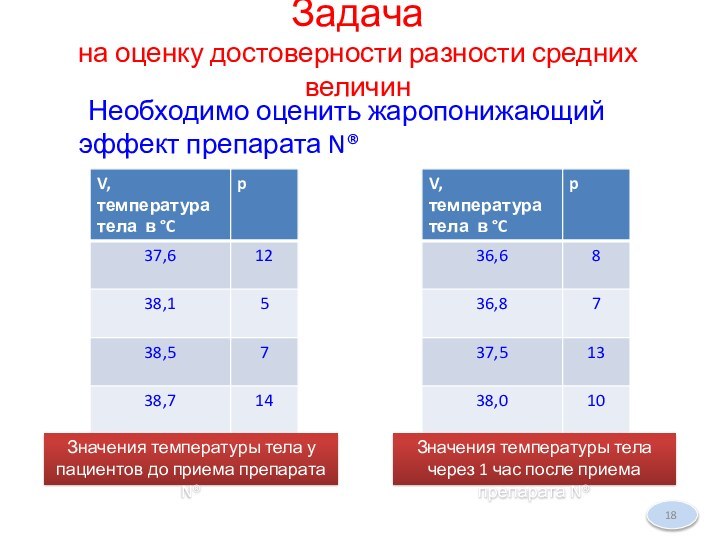
Задача
на оценку достоверности разности средних величин
Необходимо оценить жаропонижающий
эффект препарата N®
Значения температуры тела у пациентов до приема
препарата N®Значения температуры тела через 1 час после приема препарата N®