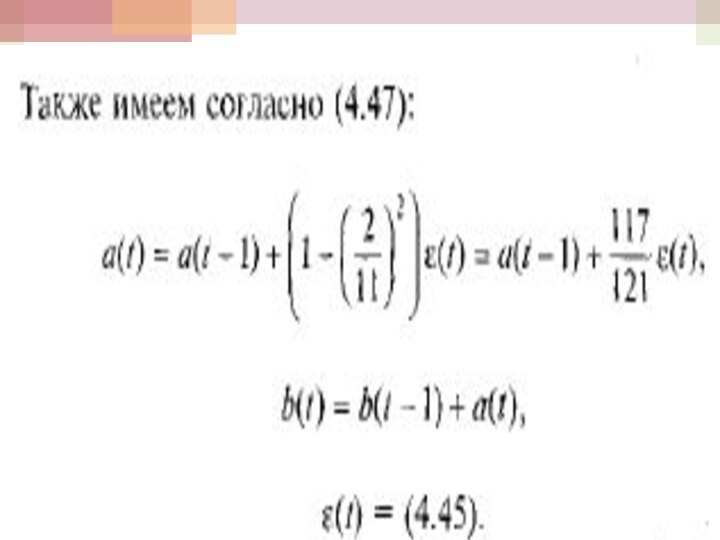Слайд 2
Содержание
Функции тренда. Виды моделей. (4) Системы нормальных уравнений
и их решения (9).
Адаптивные модели (25).
Модели Хольта (34) и
Брауна М1 (39) .
Пример построения модели Брауна М1 (41).
Построение модели Брауна М2 (49). Ошибка прогноза (54).
Пример построения модели М2 (60). Ошибка прогноза (71).
Слайд 3
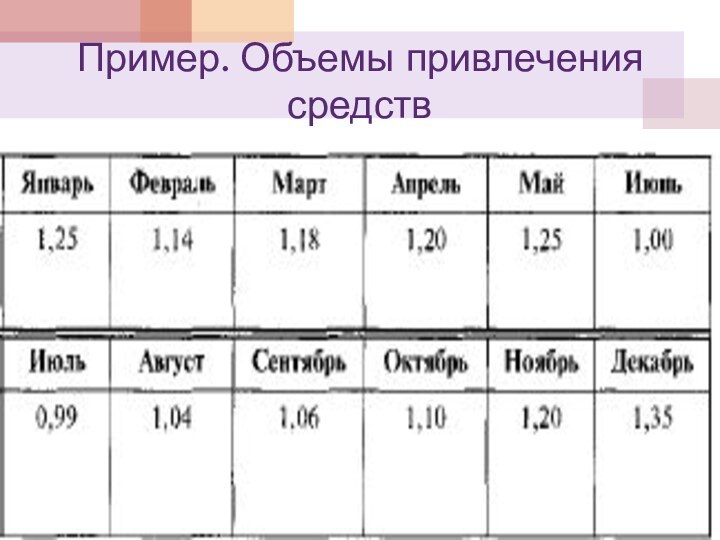
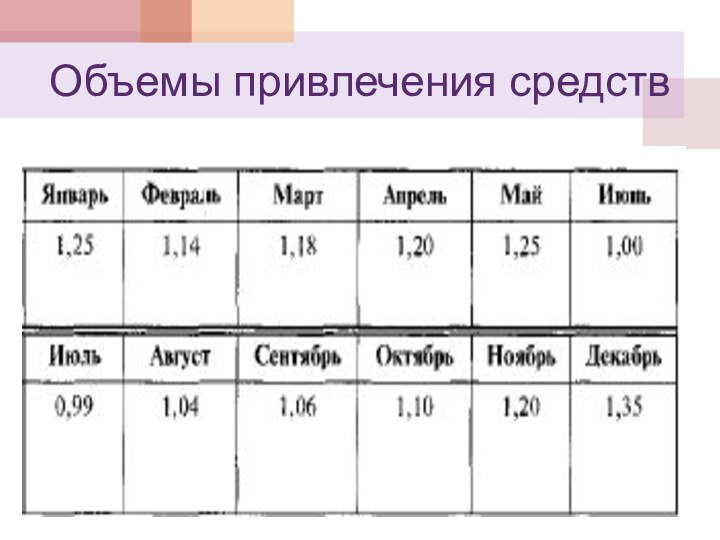
Пример. Объемы привлечения средств
Слайд 4
Функции тренда
Параметры уравнений функции тренда находят с
помощью теории корреляции методом наименьших квадратов. Наиболее распространенными в
экономике являются следующие регрессионные модели долговременных составляющих аналитической модели 4.13 ряда динамики (функции тренда)
Слайд 5
Функции тренда
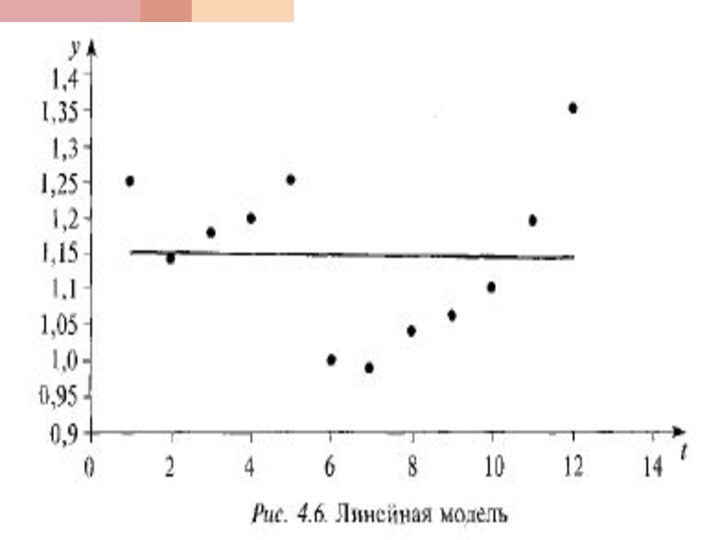
Линейная модель (4.13)
Степенная модель (4.14)
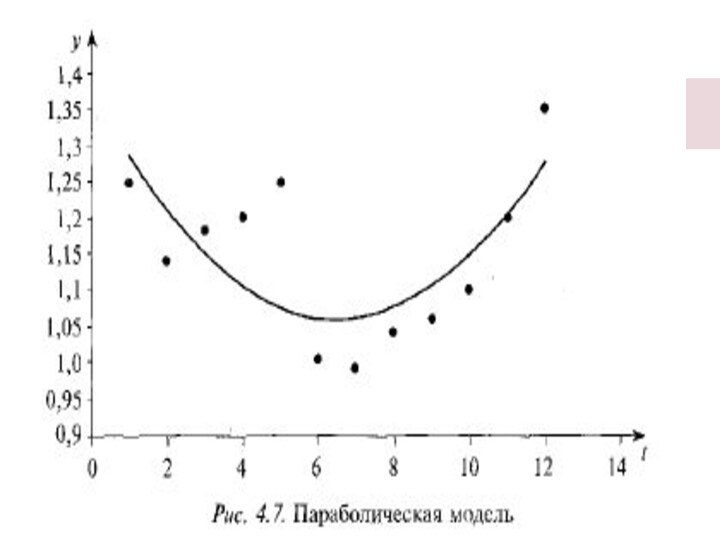
Параболическая модель (4.15)
Слайд 6
Models
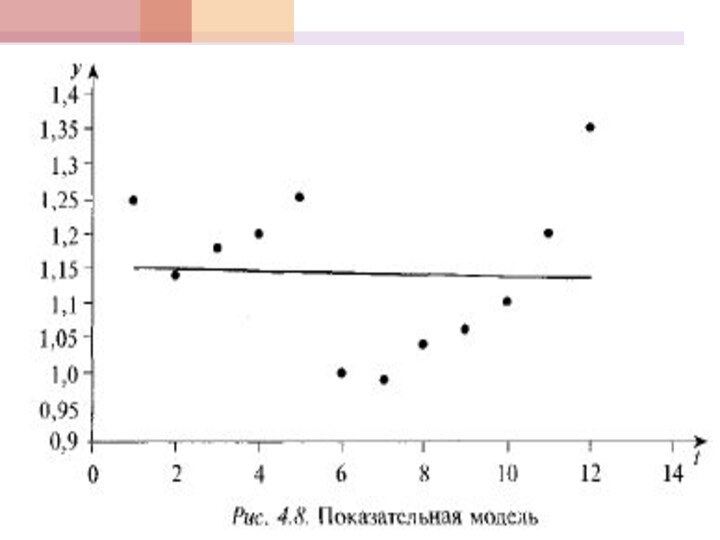
4.Показательная модель (4.16)
Слайд 7
Models
5.Смешанная модель
6.В некоторых случаях применяют более сложные виды
зависимостей между y и r
Слайд 8
Значения параметров
Значения параметров уравнений 4.13-4.19 регрессии находят с
помощью метода наименьших квадратов, решая систему нормальных уравнений.
Приведем системы
нормальных уравнений для некоторых из перечисленных моделей:
Слайд 9
Системы нормальных уравнений. Линейная модель.
Слайд 10
Система нормальных уравнений для линейной модели
Слайд 11
Нормальные уравнения. Степенная модель
Слайд 12
Нормальные уравнения. Параболическая модель.
Слайд 13
Система нормальных уравнений для показательной модели (4.16)
Слайд 14
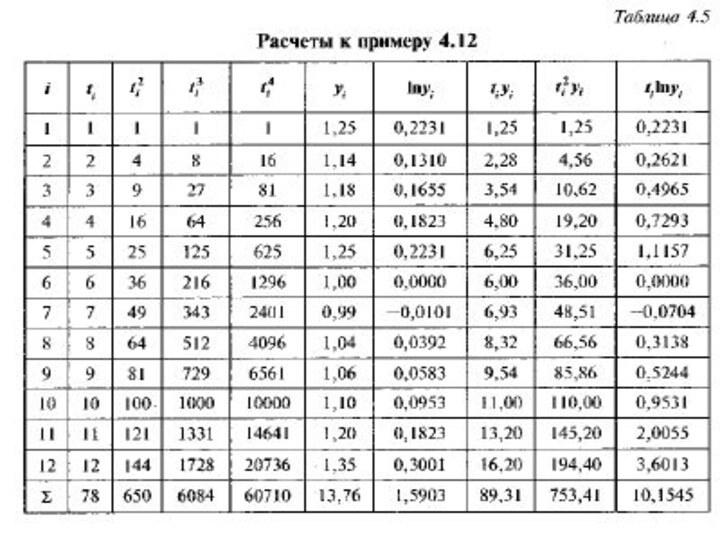
Пример 4.12. Найти функцию тренда
Для данных
из примера 4.7. найти вид уравнения функции тренда в
предположении:
а) линейной
б) параболической
в) показательной моделей
Напомним объемы привлечения средств за последние 12 месяцев и произведем все необходимые вычисления для решения систем нормальных уравнений для перечисленных моделей.
Слайд 25
3. Адаптивные модели
Рассмотренные регрессионные модели не могут приспосабливаться,
адаптироваться к новым условиям по мере изменения факторных признаков.
Кроме
того при прогнозировании имеет место фактор обесценения старой информации по мере поступления новой.
Слайд 26
Основные понятия
Например. Система находится в некотором состоянии для
определения текущего значения параметров. На их основе осуществляется прогноз
y* на h шагов.
Через h шагов становится известным фактическое значение прогнозируемого признака yi и величина его отклонения от теоретического (расчетного).
Слайд 28
Основные понятия
Это отклонение учитывают при прогнозировании на h+hi
шаг в соответствии с правилом перевода модели из одного
состояния в другое.
Процесс продолжается до тех пор. Пока параметры модели не позволят с максимальной точностью определить последнее значение уровня эмпирического ряда динамики.
Слайд 29
Основные понятия
Кроме коэффициентов уравнения модели и h используют
параметр α , называемый коэффициентом дисконтирования данных. Он изменяется
в пределах от 0 до 1.
Вместе с α используется также коэффициент сглаживания
β=1-α
Слайд 30
Основные понятия. Коэффициент дисконтирования.
Расчет выполняются двумя способами.
По первому
способу:
При этом 10
эмпирических данных.
Слайд 31
Основные понятия
Согласно второму способу берут несколько коэффициентов дисконтирования
и для одной обучающей выборки устанавливают вид моделей.
Для каждой
из них рассчитывают величину средней ошибки аппроксимации
Выбирают такое значение α , которому соответствует
Слайд 32
Основные понятия
Все адаптивные модели базируются на
двух схемах:
Авторегрессии (АР – модели)
Скользящего среднего (СС – модели)
В авторегрессионных моделях оценкой текущего уровня является взвешенная сумма не всех, а нескольких предшествующих уровней.
Информационная ценность наблюдений обуславливается не их близостью к моделируемому уровню, а теснотой связи между ними.
Слайд 33
Основные понятия
В схеме скользящей средней оценкой
текущего уровня являются взвешенные средние всех предыдущих уровней.
Информационная ценность наблюдений признается тем больше, чем ближе они находятся к концу интервала наблюдений.
Наибольшее распространение получили - СС модели
Слайд 34
3а.Модели Хольта и Брауна.
В практике статистического прогнозирования
наиболее часто используют три модели скользящего среднего ( СС
– модели):
Модель Хольта
Модель М1 Брауна
Модель М2 Брауна
Слайд 35
Модель Хольта
Модель Хольта представляет тенденцию развития признака (
в нашем случае – значений уровней ряда динамики) как
линейную тенденцию с постоянно меняющимися параметрами.
Прогнозную оценку вычисляют в момент времени t на h шагов вперед с помощью модели:
Слайд 37
Модель Хольта
Где β1 и β2 -
коэффициенты сглаживания
ε(t) - величина отклонения (4.45)
Слайд 38
Модель Хольта
Начальные значения a(0) и b(0) находят методом
наименьших квадратов (например по первым значениям уровней ряда динамики.)
Слайд 39
Модель М1 Брауна
Она предназначена для нахождения параметров модели
вида
Слайд 40
Модель М1 Брауна
Начальные значения a и b
определяются также, как и в модели Хольта т.е.
методом наименьших квадратов по первым значениям уровней ряда динамики, а ε(t) опять определяем по формуле т.е. как разность фактического и прогнозного значений
Слайд 41
4. Построение модели М1 (183)
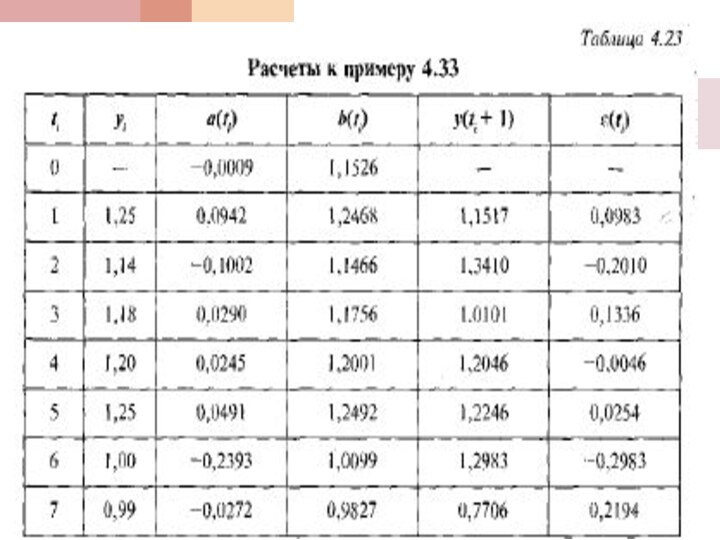
Пример 4.33
По
данным примера 4.7.:
1)построить модель М1;
2)
произвести точечный прогноз значения уровня ряда динамики (объем привлеченных средств) на февраль 2008 года
Поскольку значения уровней рассматриваемого ряда динамики отстоят один от другого на один месяц
h=1
Слайд 49
5.Модель М2 (185 4.48)
Для построения модели М2 применяют
рекуррентную формулу для нахождения экспоненциальной средней к - го
порядка:
Слайд 51
Тренд линейный. М2
Если тренд, наиболее точно описывающий эмпирические
данные, линейный с уравнением 4.13
то
Слайд 53
Уравнение адаптивной модели М2 в линейном виде
В линейном
случае уравнение адаптивной модели М2 есть (4.46) {y(t+h)=a(t)h+b(t)} в
которой:
Слайд 54
Коэффициенты линейной модели М2
В линейном случае уравнение адаптивной
модели М2. есть (4.46), в которой
Слайд 60
(Пример 4.34.) 6.Построить адаптивную модель М2
Слайд 61
Пример. Линейная модель. f1(t)= -0,0009t +1,1526
Слайд 63
Экспоненциальная средняя первого порядка
Слайд 64
Учитывая имеющуюся линейную модель
Слайд 65
из 4.20
Т.е. прогнозную оценку в момент времени t
на h шагов вычисляют с помощью модели:
y(t+h) =a(t)h
Слайд 66
Из 4.50. если тренд линейный, то
Слайд 67
Экспоненциальная средняя второго порядка
Слайд 68
Расчет коэффициентов
Согласно 4.51
Слайд 69
Из 4.51
В линейном случае уравнение адаптивной
модели М2 есть
y(t + h)= a(t)h + b(t)
В которой
Слайд 70
4.46
Т.е. прогнозную оценку в момент времени t
на h шагов вычисляют с помощью модели:
y(t+h) =a(t)h