Слайд 2
Мы научились находить первоначальный план поставок. Теперь надо
выяснить является ли найденный план оптимальным и, если нет
то как его оптимизировать. Для этого надо составить матрицу оценок.
Оценка клетки (J, j) вычисляется по следующему правилу:
оценка i-й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j)
Оценки строки и столбца выбираются таким образом, чтобы оценки всех отмеченных клеток были равны нулю. После этого оценки всех клеток записываются в виде матрицы — матрицы оценок. Если матрица оценок не содержит отрицательных чисел, то получен оптимальный план поставок. Иначе проводится оптимизация плана поставок.
Слайд 3
Двигаясь из клетки с отрицательной оценкой по отмеченным
клеткам (причем запрещается делать два последовательных шага в одной
строке или в одном столбце), строят так называемый цикл пересчета. Внутри этого цикла перераспределяют поставки. Для полученной таблицы находят матрицу оценок и т. д.
Рассмотрим подробнее эту схему на конкретном примере.
Слайд 4
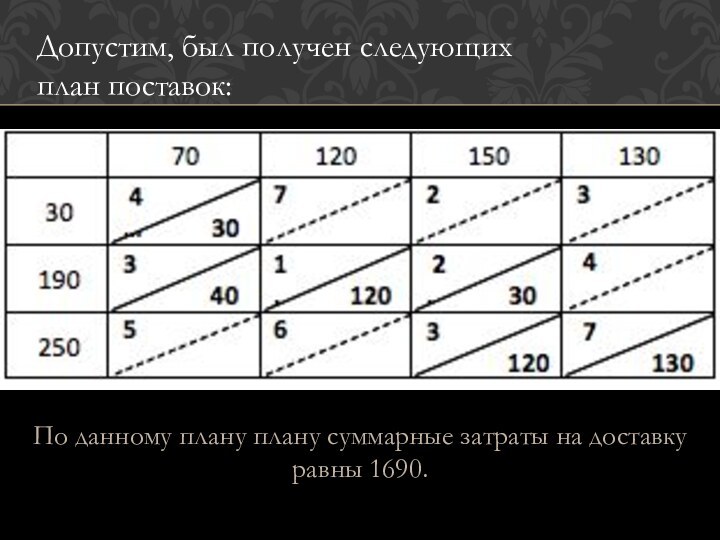
Допустим, был получен следующих план поставок:
По данному
плану плану суммарные затраты на доставку равны 1690.
Слайд 5
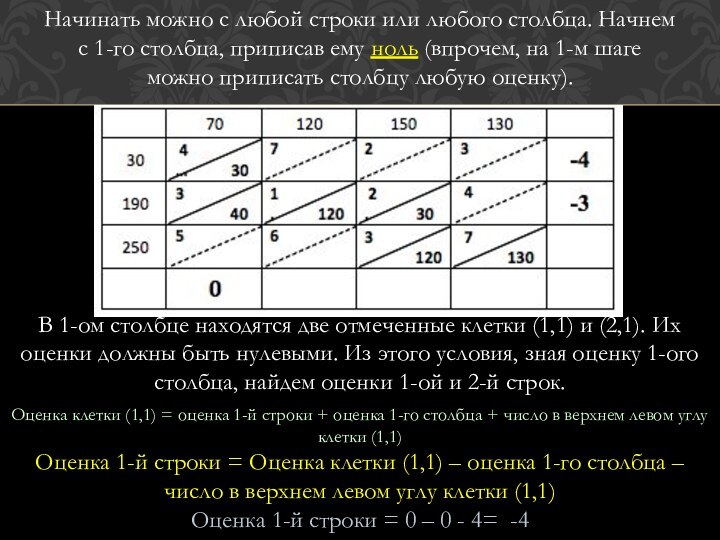
Начинать можно с любой строки или любого столбца.
Начнем с 1-го столбца, приписав ему ноль (впрочем, на
1-м шаге можно приписать столбцу любую оценку).
В 1-ом столбце находятся две отмеченные клетки (1,1) и (2,1). Их оценки должны быть нулевыми. Из этого условия, зная оценку 1-ого столбца, найдем оценки 1-ой и 2-й строк.
Оценка клетки (1,1) = оценка 1-й строки + оценка 1-го столбца + число в верхнем левом углу клетки (1,1)
Оценка 1-й строки = Оценка клетки (1,1) – оценка 1-го столбца – число в верхнем левом углу клетки (1,1)
Оценка 1-й строки = 0 – 0 - 4= -4
Слайд 6
Так же найдем оценку 2-й строки:
Оценка клетки (2,1)
= оценка 2-й строки + оценка 1-го столбца +
число в верхнем левом углу клетки (2,1)
Оценка 2-й строки = Оценка клетки (2,1) – оценка 1-го столбца – число в верхнем левом углу клетки (2,1)
Оценка 2-й строки = 0 – 0 - 3= -3
Слайд 7
Теперь надо найти отмеченную клетку, для которой известны
оценка строки или оценка столбца.
Например, это клетка (2,2).
Для нее
известна оценка строки.
Оценка клетки (2,2) = оценка 2-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (2,2) =
0 = (-3) + оценка 2-го столбца + 1
Оценка 2-го столбца = 2
Слайд 8
Для отмеченной клетки (2,3) мы знаем только оценку
строки.
Попробуйте найти оценку 3-го столбца.
Оценка клетки (2,3) = оценка
2-й строки + оценка 3-го столбца + 2 = 0
??
Слайд 9
Оценка клетки (2,3) = оценка 2-й строки +
оценка 3-го столбца + 2 = 0
Оценка 2-й строки
= 1
Получаем следующую таблицу:
Попробуйте самостоятельно найти оценку 3-й строки и оценку 4-го столбца.
Слайд 10
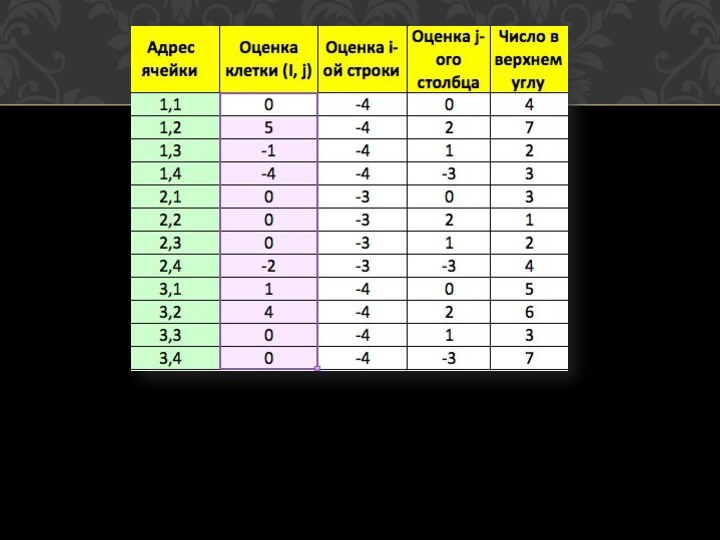
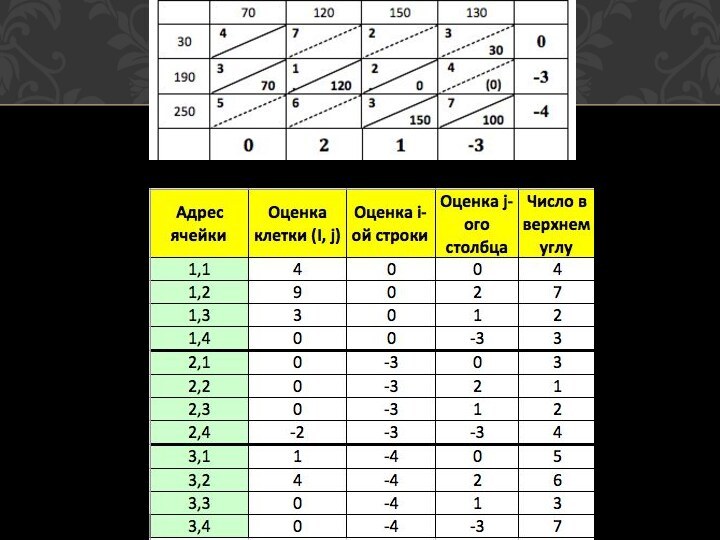
Найдены оценки всех строк и столбцов. Вычислим оценки
всех клеток и составим матрицу оценок.
Слайд 11
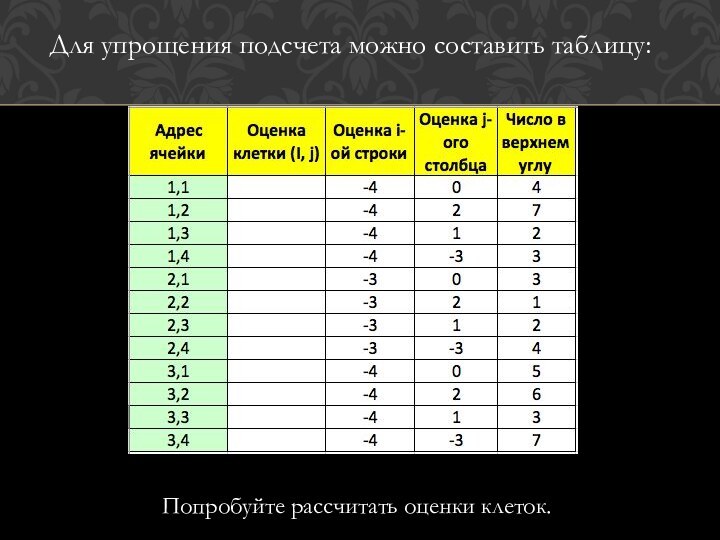
Для упрощения подсчета можно составить таблицу:
Попробуйте рассчитать оценки
клеток.
Слайд 13
Так как матрица оценок содержит отрицательные числа, то
наш план является неоптимальным.
Проведем его оптимизацию.
Выбираем клетку с наименьшей
оценкой. Это клетка (1,4). Ее оценка -4.
Наша задача – построить цикл пересчета.
Выходя из клетки (1,4) и двигаясь ТОЛЬКО ПО ОТМЕЧЕННЫМ КЛЕТКАМ, нужно вернуться в стартовую клетку (1,4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце.
Слайд 14
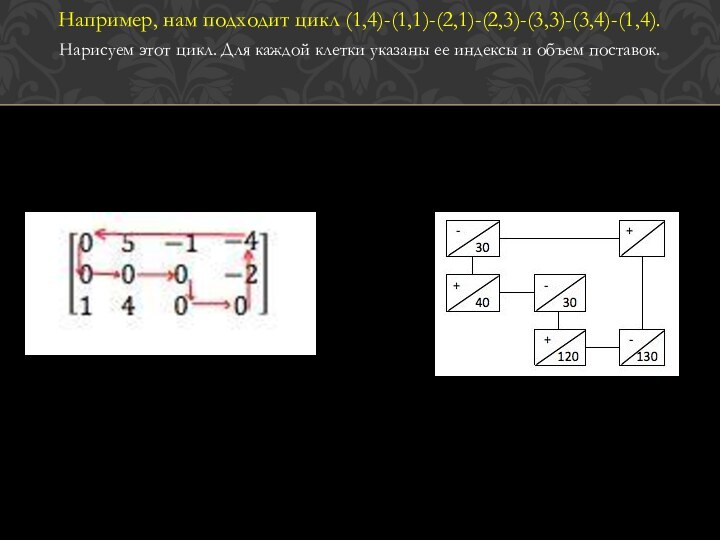
Например, нам подходит цикл (1,4)-(1,1)-(2,1)-(2,3)-(3,3)-(3,4)-(1,4).
Нарисуем этот цикл. Для
каждой клетки указаны ее индексы и объем поставок.
Слайд 15
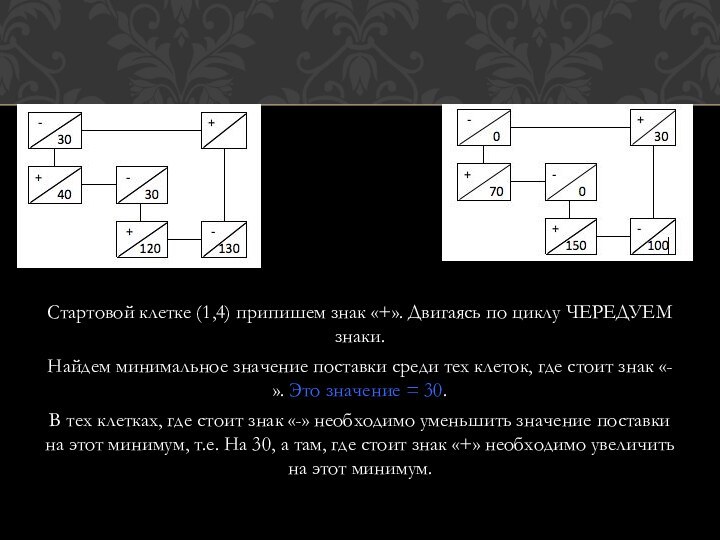
Стартовой клетке (1,4) припишем знак «+». Двигаясь по
циклу ЧЕРЕДУЕМ знаки.
Найдем минимальное значение поставки среди тех
клеток, где стоит знак «-». Это значение = 30.
В тех клетках, где стоит знак «-» необходимо уменьшить значение поставки на этот минимум, т.е. На 30, а там, где стоит знак «+» необходимо увеличить на этот минимум.
Слайд 16
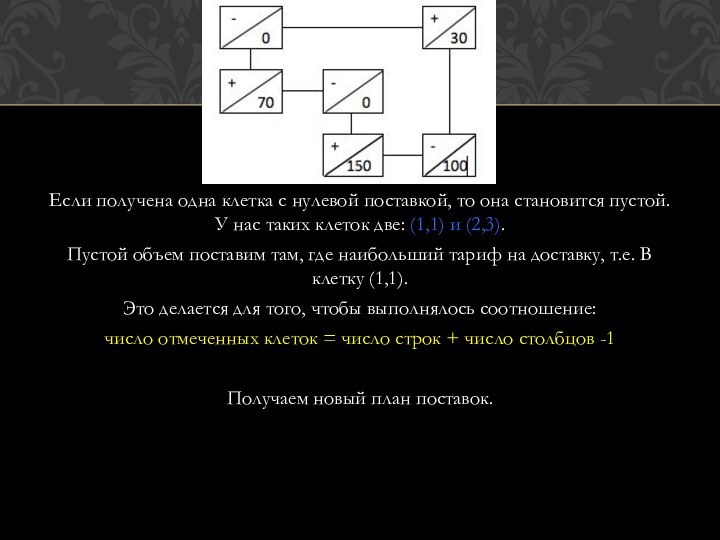
Если получена одна клетка с нулевой поставкой, то
она становится пустой. У нас таких клеток две: (1,1)
и (2,3).
Пустой объем поставим там, где наибольший тариф на доставку, т.е. В клетку (1,1).
Это делается для того, чтобы выполнялось соотношение:
число отмеченных клеток = число строк + число столбцов -1
Получаем новый план поставок.
Слайд 17
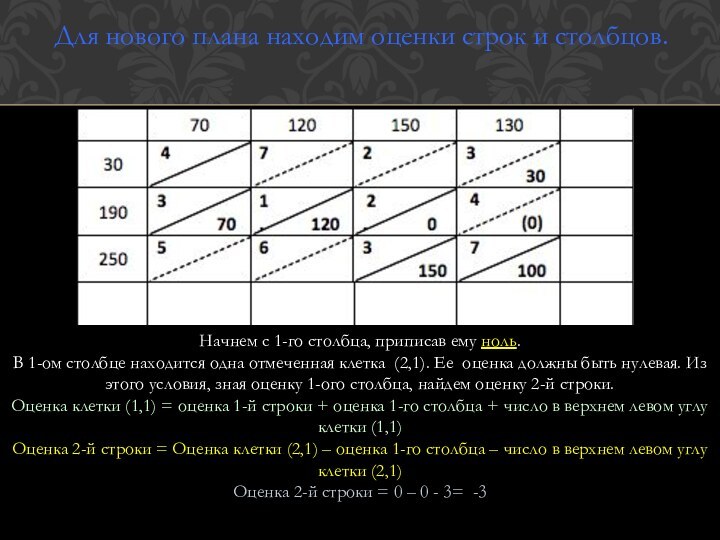
Для нового плана находим оценки строк и столбцов.
Начнем
с 1-го столбца, приписав ему ноль.
В 1-ом столбце
находится одна отмеченная клетка (2,1). Ее оценка должны быть нулевая. Из этого условия, зная оценку 1-ого столбца, найдем оценку 2-й строки.
Оценка клетки (1,1) = оценка 1-й строки + оценка 1-го столбца + число в верхнем левом углу клетки (1,1)
Оценка 2-й строки = Оценка клетки (2,1) – оценка 1-го столбца – число в верхнем левом углу клетки (2,1)
Оценка 2-й строки = 0 – 0 - 3= -3
Слайд 18
Для нового плана находим оценки строк и столбцов.
Для
клетки (2,2) известна оценка строки.
Оценка клетки (2,2) = оценка
2-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (2,2) =
0 = (-3) + оценка 2-го столбца + 1
Оценка 2-го столбца = 2
Слайд 20
План является неоптимальным, т.к. Оценка клетки (2,4) меньше
0.
Строим для него цикл пересчета.
Составляем матрицу оценок:
Min = 0.
Клетка
(2.3) становится пустой, а клетка (2,4) – ОТМЕЧЕННОЙ (нулевая поставка).
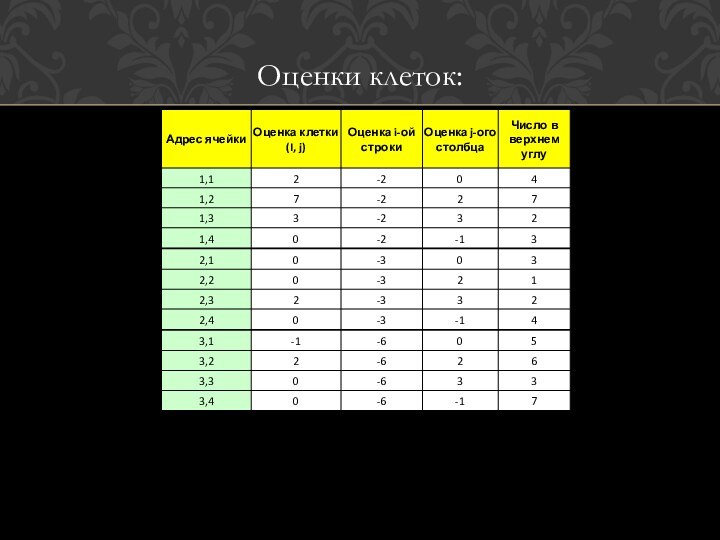
Слайд 21
Найдите оценки клеток.
Оценка клетки (J, j) вычисляется по
следующему правилу:
оценка i-й строки + оценка j-го столбца
+ число в левом верхнем углу клетки (i, j)
Получаем новый план поставок:
Слайд 23
План является неоптимальным, т.к. Оценка клетки (3,1) меньше
0.
Постройте цикл пересчета.
Получаем следующую матрицу оценок:
Минимум (70,100) = 70.
В
клетках со знакам «+» поставки увеличиваются на 70, а в клетках со знаком «-» поставки уменьшаются на 70.
Клетка (2,1) становится пустой.
Нам подходит цикл (3,1)-(2,1)-(2,4)-(3,4)-(3,1)
Слайд 24
Поучаем новый план поставок:
Составим матрицу оценок:
Матрица оценок не
содержит отрицательных чисел.
Получен оптимальный план поставок.
Слайд 25
Суммарные затраты на перевозку груза равны:
Напомню, что суммарные
затраты на перевозку груза 1690.
Слайд 26
Открытая модель сводится к закрытой.
Если суммарная мощность
поставщиков больше суммарного спроса потребителей, то вводится фиктивный потребитель,
которому приписывается спрос, равный разнице между суммарной мощностью поставщиков и суммарным спросом потребителей.
Полученная закрытая модель решается.
ОКТРЫТАЯ МОДЕЛЬ