Слайд 2
Цель: (образовательная)
создать условия для развития мыслительных операций,
путём использования нестандартных заданий.
:(личная)
не потерять ребёнка с его
живыми глазами и желанием учиться;
не спешить учить, а спешить научить
детей учиться.
Слайд 3
Задачи:
Способствовать развитию мыслительных операций: сравнение, анализ,
синтез, классификация, абстрагирование и обобщение.
Познакомить учащихся с приёмами решения
нестандартных заданий.
Способствовать развитию интеллектуальных способностей.
Повысить интерес учащихся к изучению математики
Слайд 4
Для достижения цели надо:
не бояться заглядывать вперёд;
использовать
занимательный материал;
видеть успех ученика и отмечать его;
радоваться вместе
с детьми успеху слабого ученика;
учить видеть связь задач с жизненными ситуациями.
Слайд 5
Для достижения цели надо:
не бояться заглядывать вперёд;
использовать
занимательный материал;
видеть успех ученика и отмечать его;
радоваться вместе
с детьми успеху слабого ученика;
учить видеть связь задач с жизненными ситуациями.
Слайд 6
Система развивающих заданий по формированию логического мышления у
младших школьников на уроках математики.
задания должны носить
развивающий характер;
задания должны располагаться в определённой
последовательности и должны быть связаны между собой;
должно прослеживаться постепенное усложнение заданий и повышение уровня самостоятельности учащихся в процессе их выполнения;
Слайд 7
задания должны быть во взаимосвязи с ранее усвоенными
знаниями, умениями и навыками;
вопросы в заданиях должны быть нацелены
на развития мыслительных операций учащихся, включать их в творческую деятельность,
содействовать их развитию.
Слайд 8
План работы
Стартовая диагностика
Применение заданий на развитие логики
на уроках математики
Итоговая диагностика
Слайд 9
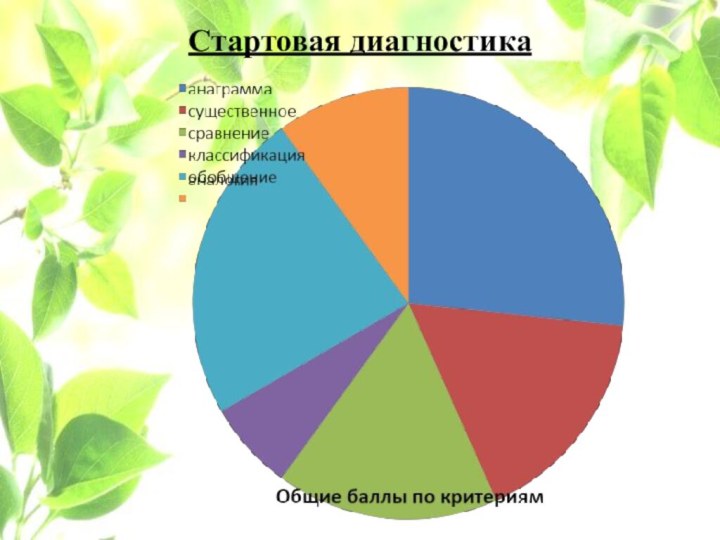
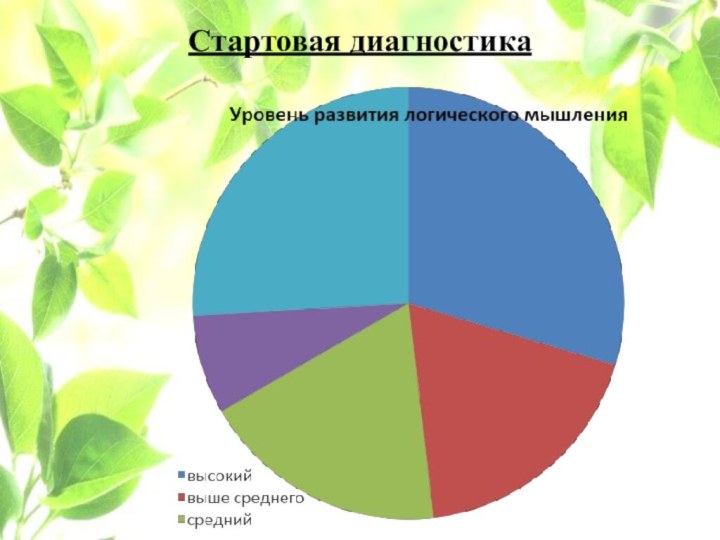
Стартовая диагностика
Диагностика включает в себя 6 критериев:
Анаграмма
теоретический анализ
с помощью анаграммы
Сравнение
способность выделять существенное
Классификация
умение обобщать
Обобщение
Аналогия
анализ отношений понятий
Слайд 12
Задания на уроках математики
Логические цепочки:
… 5 7 9…
(Ответ:
1,3,5, 7, 9, 11, 13).
Игра «Лишнее число».
Даны числа: 1, 10, 6. Какое число лишнее?
Лишним может быть число 1, так как это нечетное число, а 10 и 6 четное.
Даже лишним может быть число 10, так как оно двузначное, а 1 и 6 однозначные.
Да и число 6 может быть лишним, так как для написания двух других использована единица.
Исключи лишнее
Дуб, дерево, ольха, ясень;
Ответ: дерево лишнее слово – остальные обозначают название деревьев.
Горький, горячий, кислый, солёный, сладкий;
Ответ: горячий.
Минута, секунда, час, вечер
Ответ: вечер – лишнее слово
Слайд 14
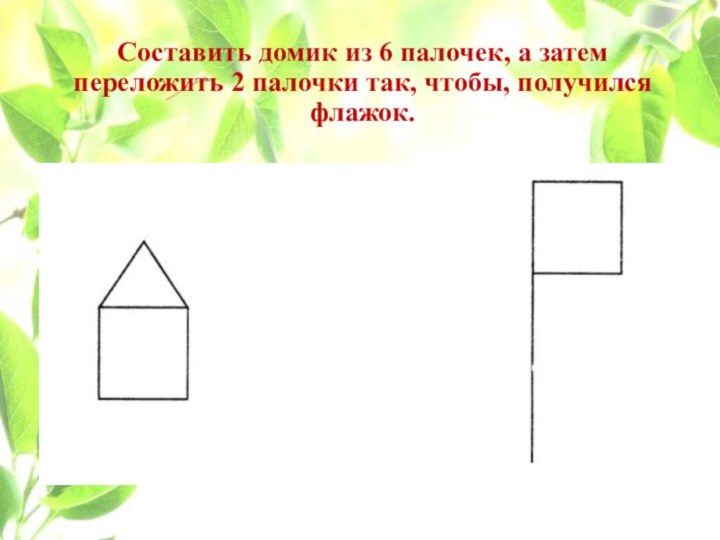
Составить домик из 6 палочек, а затем переложить
2 палочки так, чтобы, получился флажок.
Слайд 15
Задача – шутка
Выглянув в окно на повороте,
Ира заметила, что перед нею 4 вагона, а за
нею 10. Сколько всего вагонов в этом поезде?
Слайд 16
Превращалка.
Пирог четырёхугольной формы надо превратить двумя
разрезами на 4 части так, чтобы 2 куска были
треугольной формы и 2 – четырёхугольной формы.
Слайд 17
Головоломка
К разложенным на столе четырём палочкам
приложите ещё шесть палочек так, чтобы получилось три.
Слайд 18
Шифровалка
Используя названия фигур, прочтите слово –
название животного.
Слайд 19
Решение задачи путём моделирования
На столе у
учителя лежало 10 тетрадей, из них 5 тетрадей в
клетку, а 6 тетрадей в зелёной обложке. Сколько тетрадей в клетку могло быть с зелёной обложкой?»
Слайд 20
Заключение.
Использование нестандартных заданий способствует развитию мыслительных операций, таких
как: обобщение, анализ, синтез, сравнение, классификация, абстрагирование.
Используя на уроках
такие виды заданий, я заметила, что учащиеся с интересом выполняют предложенные задания, лучше усваивают учебный материал, таким образом, процесс обучения математике не сводится только к вычислительным действиям, а становится основой развития личности ребёнка.
Слайд 21
Заключение.
Используемые задания позволяют активизировать творческие способности учащихся при
решении математических задач.
Рекомендуемые задания позволяют научить детей решать логические
задачи, строить дедуктивные умозаключения, разрешать проблемные ситуации и добиваться оригинальности решений.