- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему СОРТИРОВКА МАССИВОВ
Содержание
- 2. Сортировка- упорядочивание данных по некоторому признаку.Сортировка-процесс размещения
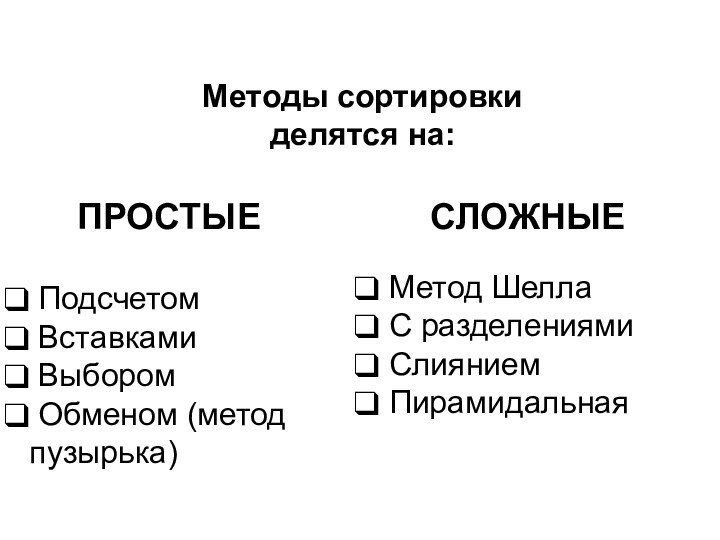
- 3. Методы сортировкиделятся на:ПРОСТЫЕСЛОЖНЫЕ Подсчетом Вставками Выбором Обменом (метод пузырька) Метод Шелла С разделениями Слиянием Пирамидальная
- 4. СОРТИРОВКА ПОДСЧЕТОММесто каждого элемента в отсортированном массиве
- 5. Исходный массив12325619203103561012192032Упорядоченный массив1 место(0 элем)2 место(1 элем)3
- 6. алг.Сортировка подсчетом {подсчитываем значение k [i] для
- 7. Метод вставок.- создается новый массив, в который мы
- 8. На j-ом этапе мы "вставляем" j-ый элемент M[j] в нужную позицию
- 10. Чтобы сделать процесс перемещения элемента M[j], более простым,
- 12. Swap- простая процедура, меняет 2 элемента местами.
- 13. Сортировка посредством выбораИдея сортировки: на j-ом этапе выбирается
- 14. алг.Сортировка выбором {Находим минимальный элемент массива и
- 15. Сказанное можно описать следующим образом:нц для j
- 17. Метод обмена или метод пузырькаПри первом проходе
- 19. упорядочение массива M[1..N]:
- 20. Все вышерассмотренные алгоритмы сортировки обладают очень серьезным
- 21. Быстрая сортировка. Метод разделения (алгоритм "быстрой" сортировки,
- 22. Пример. Быстрая сортировка по возрастанию массива A
- 23. Сортировка методом Шелла.Основная идея этого алгоритма заключается
- 24. program shell; uses crt; const lens=10; //* Количество
- 25. Метод разделения (алгоритм "быстрой" сортировки, метод Хоара)Метод
- 26. Он построен по принципу «разделяй и властвуй»,
- 28. Merge Sort (или Сортировка слиянием) - одна из самых
- 29. Для сортировки со слиянием массива a[1], a[2],
- 30. Программа сортировка слиянием на языке программирования pascal const
- 31. unit uMergeSort; interfacetype TItem = Integer;
- 32. //Процедура сортировки слияниямиprocedure MergeSort(var Arr: TArray);var tmp
- 33. //Просто дописываем в tmp оставшиеся эл-ты if i
- 34. //Сортировка procedure sort(L, R : Integer); var
- 35. Сортировка включением состоит в следующем: выбирается некоторый
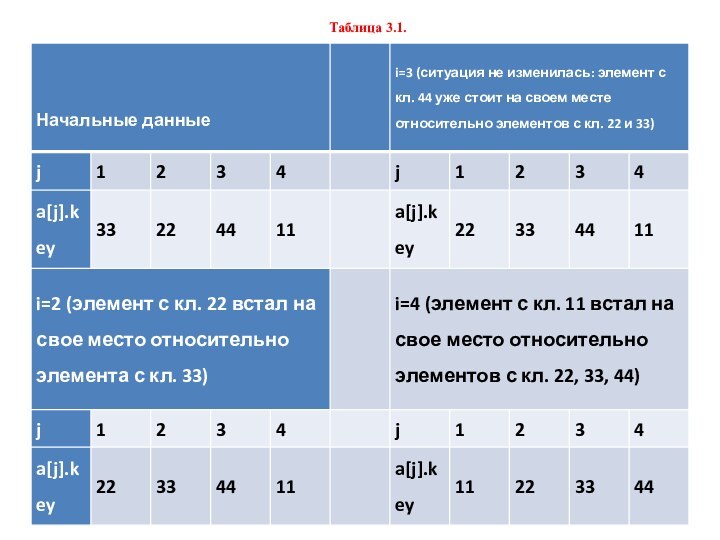
- 36. Таблица 3.1.
- 37. У этого алгоритма есть одно важное достоинство:
- 38. Усовершенствованная сортировка включением известна как сортировка Шелла.
- 39. После того, как отсортированы непересекающиеся h-серии, процесс возобновляется с новым значением h’
- 40. Procedure ShellSort; var h,j,k,y,kh:integer; buf:node; begin h:=1;
- 41. Пирамидальная сортировка Пирамидальная сортировка является улучшенным вариантом
- 42. для всякого i = L, …, R/2.
- 44. Бинарное (двоичное) дерево (binary tree) - это
- 46. Бинарное дерево может представлять собой пустое множество, и может выродиться в список. Вырожденное бинарное дерево:
- 47. Структура для создания корня и узлов дерева
- 48. Здесь поля Left и Right - это указатели на потомков данного
- 49. Эта процедура добавляет элемент X к дереву, учитывая величину X. При этом создается новый узел дерева.
- 50. Дерево, изображенное на рисунке 2, представляет собой
- 52. Способ построения пирамиды «на том же месте»
- 53. Добавляемый ключ K[2] просеивается в пирамиду: его
- 54. В нашем примере получалось так, что оба
- 55. Рисунок 12.6 Просеивание ключа 44 в пирамиду
- 56. Достоинства: Имеет доказанную оценку худшего случая O.
- 57. procedure Sort(var Arr: array of SomeType; Count:
- 58. begin While index < Count div 2
- 59. //Основная функция var i: integer; Current: SomeType;
- 61. Это дерево состоит из семи узлов, и
- 62. Скачать презентацию
- 63. Похожие презентации
Сортировка- упорядочивание данных по некоторому признаку.Сортировка-процесс размещения заданного множества объектов в определенном порядке (убывания или возрастания)Сортировка- один из наиболее распространенных процессов современной обработки информации. Это распределение элементов множества по группам в соответствии с определенными правилами.



![СОРТИРОВКА МАССИВОВ алг.Сортировка подсчетом {подсчитываем значение k [i] для каждого элемента массива a}](/img/tmb/14/1362383/7b4c635e2393672ea699701da4490dbf-720x.jpg)



![СОРТИРОВКА МАССИВОВ Чтобы сделать процесс перемещения элемента M[j], более простым, полезно воспользоваться барьером: ввести](/img/tmb/14/1362383/d7768068167cafc1da551deafc612808-720x.jpg)


![СОРТИРОВКА МАССИВОВ Сортировка посредством выбораИдея сортировки: на j-ом этапе выбирается элемент наименьший среди M[j], M[j+1],..., M[N] и меняется](/img/tmb/14/1362383/1ca0c0d46dc5ed57b103d2b2a81f4dc2-720x.jpg)
![СОРТИРОВКА МАССИВОВ алг.Сортировка выбором {Находим минимальный элемент массива и его индекс} min:=a[1]](/img/tmb/14/1362383/69906536d1c631ba711d69e151a85c24-720x.jpg)



![СОРТИРОВКА МАССИВОВ упорядочение массива M[1..N]:](/img/tmb/14/1362383/258bfeb61dbcd06ec5ed12e3c87a4f2c-720x.jpg)








![СОРТИРОВКА МАССИВОВ Для сортировки со слиянием массива a[1], a[2], ..., a[n] заводится парный массив](/img/tmb/14/1362383/0e24e7d2f44770d7adebbf67384a502e-720x.jpg)
![СОРТИРОВКА МАССИВОВ Программа сортировка слиянием на языке программирования pascal const n=10;var a,c:array[1..n] of integer;t:integer;... Procedure Sliv(a1,k,b:integer);](/img/tmb/14/1362383/f03c7f3e0b4b538159ebc7e741bffb03-720x.jpg)










![СОРТИРОВКА МАССИВОВ для всякого i = L, …, R/2. Если имеется массив K[1], K[2],](/img/tmb/14/1362383/bb1adcee48dc0c5e7e5dc86836f31301-720x.jpg)






![СОРТИРОВКА МАССИВОВ Добавляемый ключ K[2] просеивается в пирамиду: его значение сравнивается с ключами узлов-сыновей,](/img/tmb/14/1362383/b6b42d20a86f64a36e3ad047f420470c-720x.jpg)







Слайд 2
Сортировка- упорядочивание данных по некоторому признаку.
Сортировка-процесс размещения заданного
множества объектов в определенном порядке (убывания или возрастания)
из наиболее распространенных процессов современной обработки информации. Это распределение элементов множества по группам в соответствии с определенными правилами.
Слайд 3
Методы сортировки
делятся на:
ПРОСТЫЕ
СЛОЖНЫЕ
Подсчетом
Вставками
Выбором
Обменом (метод
пузырька)
Метод Шелла
С разделениями
Слиянием
Пирамидальная
Слайд 4
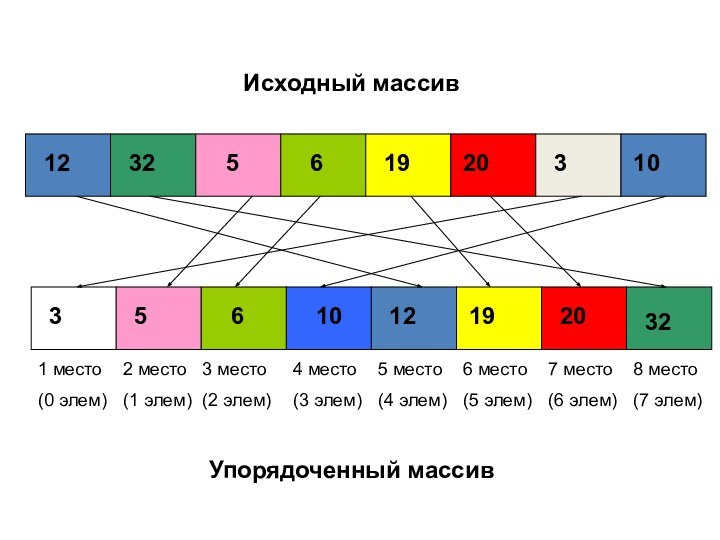
СОРТИРОВКА ПОДСЧЕТОМ
Место каждого элемента в отсортированном массиве зависит
от количества элементов, меньших его- для сортировки надо для
каждого элемента массива подсчитать к-во эл-тов, меньших его, и затем разместить каждый рассмотренный элемент на соответствующем месте в новом, специально созданном , массиве.Например, если значение некоторого элемента исходного массива превышает значения четырех других, то его место в упорядоченной последовательности- пятое.
Слайд 5
Исходный массив
12
32
5
6
19
20
3
10
3
5
6
10
12
19
20
32
Упорядоченный массив
1 место
(0 элем)
2 место
(1 элем)
3 место
(2
элем)
4 место
(3 элем)
5 место
(4 элем)
6 место
(5 элем)
7 место
(6 элем)
8
место(7 элем)
Слайд 6
алг.Сортировка подсчетом
{подсчитываем значение k [i] для каждого
элемента массива a}
нц для I от 1
до nk [i]:=0
кц
нц для I от 2 до n
нц для j от 1 до i-1
если a [i] то {увеличиваем значение к для j-го элемента}
k [j]:= k [j] +1
иначе {увеличиваем значение k для i-го элемента}
k [i]:= k [i] +1
все
кц
кц
{размещаем все элементы массива а на соответствующих им местах в массиве b
нц для I от 1 до n
b [k [i] + 1]:=a [i] {позиция в массиве больше на 1 кол-ва меньших по величине числ}
кц
кон
Слайд 7 Метод вставок.- создается новый массив, в который мы последовательно
вставляем элементы из исходного массива так, чтобы новый массив
был упорядоченным. Вставка происходит следующим образом: в конце нового массива выделяется свободная ячейка, далее анализируется элемент, стоящий перед пустой ячейкой (если, конечно, пустая ячейка не стоит на первом месте), и если этот элемент больше вставляемого, то подвигаем элемент в свободную ячейку (при этом на том месте, где он стоял, образуется пустая ячейка) и сравниваем следующий элемент.Так мы прейдем к ситуации, когда пустая ячейка стоит в начале массива. После последней вставки мы получим упорядоченный исходный массив.
Слайд 8 На j-ом этапе мы "вставляем" j-ый элемент M[j] в нужную позицию среди
элементов M[1], M[2],..., M[j-1], которые уже упорядочены. После этой вставки первые j элементов массива M будут
упорядочены. Сказанное можно записать следующим образом:нц для j от 2 до N переместить M[j] на позицию i <= j такую, что M[j] < M[k] для i<= k < j и либо M[j] >= M[i-1], либо i=1 кц
перед вставкой M[j], в позицию i-1 надо проверить, не будет ли i=1. Если нет, тогда сравнить M[j] ( который в этот момент будет находиться в позиции i) с элементом M[i-1].
Слайд 10 Чтобы сделать процесс перемещения элемента M[j], более простым, полезно
воспользоваться барьером: ввести "фиктивный" элемент M[0], чье значение будет заведомо меньше
значения любого из «реальных» элементов массива (как это можно сделать?). Мы обозначим это значение через —оо.
Слайд 12
Swap- простая процедура, меняет 2 элемента местами.
КОД:
Procedure Swap(Var
a, b: integer); Var p: integer; begin p := a; a
:= b; b := p; end;
Слайд 13
Сортировка посредством выбора
Идея сортировки: на j-ом этапе выбирается элемент
наименьший среди M[j], M[j+1],..., M[N] и меняется местами с элементом M[j].
В результате
после j-го этапа все элементы M[j], M[j+1],...,M[N]будут упорядочены.
Слайд 14
алг.Сортировка выбором
{Находим минимальный элемент массива и его
индекс}
min:=a[1] indmin:= 1
нц для
j от 2 до nесли a [j] < a [indmin]
то {увеличиваем значение к для j-го элемента}
min:= a [j]
indmin := j
все
кц
{записываем минимальный элемент на i-е место в массиве b }
b [i] := min
{заменяем минимальный элемент исходного массива «большим числом»
b [i] := max
Кц
{выводим на экран отсортированный массив b}
нц для I от 1 до n
вывод b [i]
кц
кон
Слайд 15
Сказанное можно описать следующим образом:
нц для j от
1 до N-1 выбрать среди M[j],..., M[N] наименьший элемент и поменять
его местами с M[j] кц
Слайд 17
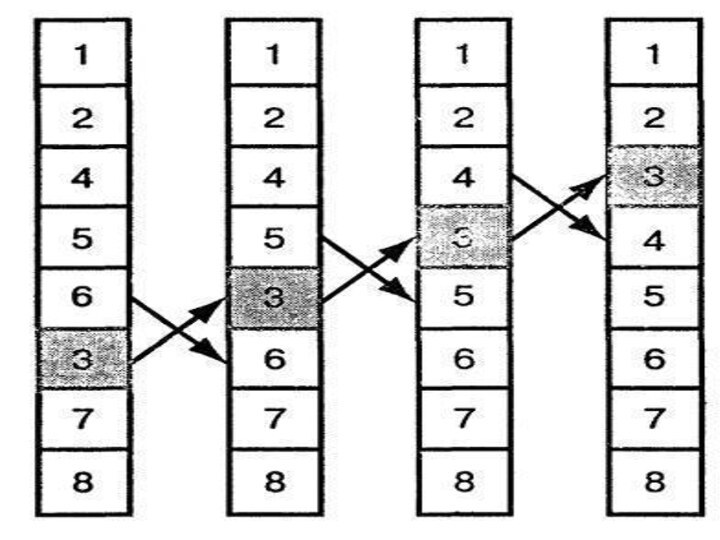
Метод обмена или метод пузырька
При первом проходе вдоль
массива, начиная проход "снизу", берется первый элемент и поочередно сравнивается с
последующими. При этом:если встречается более "легкий" (с меньшим значением) элемент, то они меняются местами;
при встрече с более "тяжелым" элементом, последний становится "эталоном" для сравнения, и все следующие сравниваются с ним. В результате наибольший элемент оказывается в самом верху массива.
Во время второго прохода вдоль массива находится второй по величине элемент, который помещается под элементом, найденным при первом проходе, т.е на вторую сверху позицию, и т.д. При втором и последующих проходах, не рассматриваются "всплывшие" элементы, т.к. они заведомо больше оставшихся, т.е. во время j-го прохода не проверяются элементы, стоящие на позициях выше j.
На рисунке изображен пример сортировки данным методом.
Слайд 20 Все вышерассмотренные алгоритмы сортировки обладают очень серьезным недостатком,
а именно, время их выполнения пропорционально квадрату числа элементов.
Для больших объемов данных эти сортировки будут медленными, а начиная с некоторой величины, они будут слишком медленными, чтобы их можно было использовать на практике.
Слайд 21 Быстрая сортировка. Метод разделения (алгоритм "быстрой" сортировки, метод
Хоара)
Как и в сортировке слиянием, массив разбивается на две
части, с условием, что все элементы первой части меньше любого элемента второй. Потом каждая часть сортируется отдельно. Разбиение на части достигается упорядочиванием относительно некоторого элемента массива, т. е. в первой части все числа меньше либо равны этому элементу, а во второй, соответственно, больше либо равны. Два индекса проходят по массиву с разных сторон и ищут элементы, которые попали не в свою группу. Найдя такие элементы, их меняют местами. Слайд 22 Пример. Быстрая сортировка по возрастанию массива A из
N целых чисел. begin X:=A[(L+R) div 2]; {В процедуру передаются левая и
правая границы сортируемого фрагмента находится, в качестве значения разбиения используется среднее значение} i:=L; j:=R; while i<=j do begin while A[i]
Слайд 23
Сортировка методом Шелла.
Основная идея этого алгоритма заключается в
том, чтобы в начале ycтpанить массовый беспорядок в массиве,
сравнивая далеко стоящие друг от друга элементы. Интервал между сравниваемыми элементами постепенно уменьшается до единицы. Это означает, что на поздних стадиях сортировка сводится просто к перестановкам соседних элементов (если, конечно, такие перестановки являются необходимыми).Слайд 24 program shell; uses crt; const lens=10; //* Количество элементов массива */ diap=100; //* Диапазон
значений */ var A:array[1 ..lens] of integer; //* Массив A */ mit:integer; //*
Переменная для перестановки .*/ str:integer; //* Шаг */ j,i:integer; BEGIN clrscr; //* Очистка экрана */ randomize; //* Инициализация случайного выбора */ for i:=1 to lens do A[i]:=random(diap); //* Заполнение массива */ st:=lens div 2; //* Вычисление шага */ for i:= 1 to lens do write(A[i],''); //* Распечатка массива */ while str>0 do //* Основной цикл с уменьшением шага */ begin for j:=lens-str downto 1 do //* Цикл по массиву */ begin i:=j; while i<=lens-str do //* Цикл сравнения через шаг */ begin if A[i]>A[i+str] then //* Если больше, */ begin mit:=A[i]; A[i]:=A[i+str]; //* то элементы меняются местами */ A[i+str]:=mit; end; i:=i+str; end; end; str:=str div 2; //* Уменьшение шага */ end; writeln; for i:=1 to lens do write(A[i],' ');//* Распечатка нового массива */ readln; END.
Слайд 25
Метод разделения (алгоритм "быстрой" сортировки, метод Хоара)
Метод быстрой
сортировки был разработан Ч. Ф. Р. Хоаром и он
же дал ему это название. В настоящее время этот метод сортировки считается наилучшим. Он основан на использовании обменного метода сортировки. Это тем более удивительно, если учесть очень низкое быстродействие сортировки пузырьковым методом, который представляет собой простейшую версию обменной сортировки.Слайд 26 Он построен по принципу «разделяй и властвуй», который
часто используется в программировании. Мы рассмотрим рекурсивную реализацию быстрой
сортировки, хотя избавится от рекурсии не представляет труда: достаточно завести стек нужного размера. Алгоритм заключается в следующем:* Выбрать один элемент массива (разделитель или барьерный элемент). *
Разбить массив на две группы: 1. элементы меньшие, чем разделитель элементы, 2. большие или равные разделителю * Рекурсивно отсортировать обе группы.
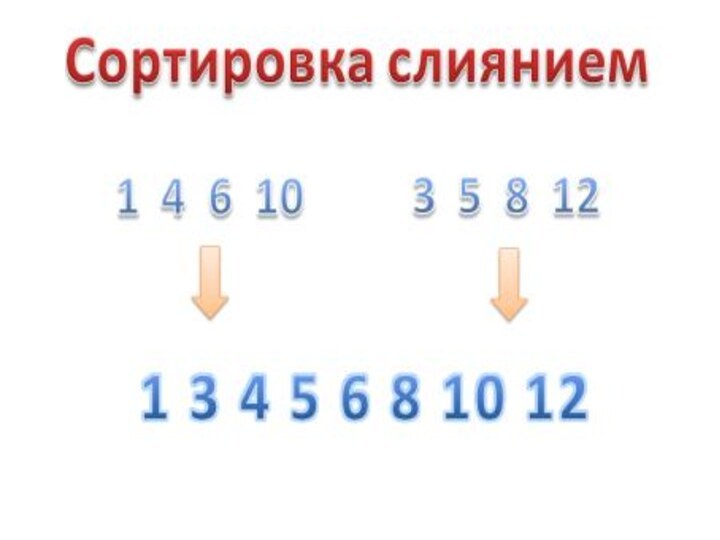
Слайд 28 Merge Sort (или Сортировка слиянием) - одна из самых популярных
методов сортирования данных в массиве.
работа данной сортировки заключена в
двух частях:
1) Разбивание массива ещё на две части (фиолетовые стрелки)
2) Постепенная сортировка уже двух отсортированных ранее частей (красные стрелки)
Рассмотрим принцип работы. Каждый раз мы делим массив на 2 части, и в конце, когда делить уже нечего, мы идём в обратном порядке, сливая два разделенных ранее частей в единую целую, и в то же время, сортируя их (причём 2 части которые сливаем уже отсортированы).
Сама процедура Merge Sort. Слайд 29 Для сортировки со слиянием массива a[1], a[2], ...,
a[n] заводится парный массив b[1], b[2], ..., b[n].
На
первом шаге производится слияние a[1] и a[n] с размещением результата в b[1], b[2], слияние a[2] и a[n-1] с размещением результата в b[3], b[4], ..., слияние a[n/2] и a[n/2+1] с помещением результата в b[n-1], b[n]. На втором шаге производится слияние пар b[1], b[2] и b[n-1], b[n] с помещением результата в a[1], a[2], a[3], a[4], слияние пар b[3], b[4] и b[n-3], b[n-2] с помещением результата в a[5], a[6], a[7], a[8], ..., слияние пар b[n/2-1], b[n/2] и b[n/2+1], b[n/2+2] с помещением результата в a[n-3], a[n-2], a[n-1], a[n]. И т.д.
На последнем шаге, например (в зависимости от значения n), производится слияние последовательностей элементов массива длиной n/2 a[1], a[2], ..., a[n/2] и a[n/2+1], a[n/2+2], ..., a[n] с помещением результата в b[1], b[2], ..., b[n].
Слайд 30
Программа сортировка слиянием на языке программирования pascal
const n=10;
var
a,c:array[1..n] of integer;
t:integer;
...
Procedure Sliv(a1,k,b:integer); {вспомогательная процедура}
var i,j,w:integer;
begin
w:=0; i:=a1; j:=k+1;
while (i
and (j<=b) doif (a[j]>a[i]) then begin inc(w); c[w]:=A[i]; inc(i); end else
begin inc(w); c[w]:=A[j]; inc(j); end;
for i:=i to k do begin inc(w); c[w]:=A[i]; end;
for j:=j to b do begin inc(w); c[w]:=A[j]; end;
w:=0;
for i:=a1 to b do begin inc(w); A[i]:=c[w]; end;
end;
Procedure Sort_Sliv(b,e:integer); {sort sliv}
var l:integer;
begin
if (e-b>1) then
begin
l:=(b+e) div 2;
if (l-b>0) then Sort_Sliv(b,l);
if (e-l>0) then Sort_Sliv(l+1,e);
Sliv(b,l,e);
end else
if (e-b=1) then if A[b]>A[e] then begin t:=A[b]; A[b]:=A[e]; A[e]:=t; end;
end;
Вызов:
Sort_Sliv(1,n);
Слайд 31
unit uMergeSort;
interface
type
TItem = Integer;
//Здесь можно написать Ваш
произвольный типTArray = array of TItem;
procedure MergeSort(var Arr: TArray);
implementation
function IsBigger(d1, d2 : TItem) : Boolean;
begin
Result := (d1 > d2); //Сравниваем d1 и d2. Не обязательно так. Зависит от Вашего типа.
//Сюда можно добавить счетчик сравнений
end;
Слайд 32
//Процедура сортировки слияниями
procedure MergeSort(var Arr: TArray);
var
tmp :
TArray; //Временный буфер // А где реализация процедуры? Этот
код работать не будет, допишите, пожалуйста//Слияние
procedure merge(L, Spl, R : Integer);
var
i, j, k : Integer;
begin
i := L;
j := Spl + 1;
k := 0;
//Выбираем меньший из первых и добавляем в tmp
while (i <= Spl) and (j <=R) do
begin
if IsBigger(Arr[i], Arr[j]) then
begin
tmp[k] := Arr[j];
Inc(j);
end
else
begin
tmp[k] := Arr[i];
Inc(i);
end;
Inc(k);
end;
Слайд 33
//Просто дописываем в tmp оставшиеся эл-ты
if
i
не пустаfor j := i to Spl do
begin
tmp[k] := Arr[j];
Inc(k);
end
else //Если вторая часть не пуста
for i := j to R do
begin
tmp[k] := Arr[i];
Inc(k);
end;
//Перемещаем из tmp в arr
Move(tmp[0], Arr[L], k*SizeOf(TItem));
end;
Слайд 34
//Сортировка
procedure sort(L, R : Integer);
var
splitter : Integer;
begin
//Массив из 1-го эл-та
упорядочен по определениюif L >= R then Exit;
splitter := (L + R) div 2; //Делим массив пополам
sort(L, splitter); //Сортируем каждую
sort(splitter + 1, R); //часть по отдельности
merge(L, splitter, R); //Производим слияние
end;
//Основная часть процедуры сортировки
begin
SetLength(tmp, Length(Arr));
sort(0, Length(Arr) - 1);
SetLength(tmp, 0);
end;
end.
Слайд 35 Сортировка включением состоит в следующем: выбирается некоторый элемент,
сортируются другие элементы, после чего выбранный элемент “включается”, т.е.
устанавливается на свое место среди других элементов. Рассмотрим подробнее соответствующий алгоритм. ... for i:=2 to n do begin buf:=a[i]; y:=a[i].key; j:=i-1; while (j>0) and (a[j].key>y) do begin a[j+]:=a[j]; j:=j-1 end a[j+1]:=buf; end ... Таблица 3.1 иллюстрирует работу сортировки включением.Слайд 37 У этого алгоритма есть одно важное достоинство: в
противоположность другим методам он имеет наилучшую эффективность, если в
начальном массиве уже установлен некоторый порядок. Пример. Если элемент с ключом 44 уже стоял на своем месте относительно элементов с ключами 22 и 33 (см. табл. 3.1), то на третьем шаге его не понадобилось передвигать. Пример. Чтобы поставить элемент с ключом 11 на свое место (см. табл. 3.1), на четвертом шаге пришлось передвинуть элементы с ключами 22, 33, 44.Слайд 38 Усовершенствованная сортировка включением известна как сортировка Шелла. В
1959 году Д.Л.Шелл предложил вместо систематического включения элемента с
индексом i в подмассив предшествующих ему элементов (этот способ противоречит принципу “балансировки”, почему и не позволяет получить эффективный алгоритм) включать этот элемент в подсписок, содержащий элементы с индексами i-h, i-2h, i-3h и т.д., где h - некоторая натуральная постоянная. Таким образом формируется массив, в котором h-серии элементов, отстоящих друг от друга на расстояние h, сортируются отдельно:Слайд 39 После того, как отсортированы непересекающиеся h-серии, процесс возобновляется
с новым значением h’
h значительно ускоряет сортировку серий с расстоянием h’. Для достаточно больших массивов результаты тестов показывают, что рекомендуемой можно считать последовательность таких hi, что hi+1=3 hi +1: ..., 364, 121, 40, 13, 4, 1. Начать процесс следует с такого элемента этой последовательности, который является ближайшим к целой части числа (n/9), превосходящим это число. Пример. Если сортируется последовательность из n=1000 элементов, то целая часть числа (n/9) составит 111, значит h следует выбрать равным 121. Ниже представлена процедура, реализующая метод Шелла.Слайд 40 Procedure ShellSort; var h,j,k,y,kh:integer; buf:node; begin h:=1; while h
do h:=3*h+1; while h>0 do begin for k:=1 to h do begin kh:=k+h; while (kh
do begin buf:=a[kh]; y:=buf.key; j:=kh-h; while (j>=1) and (yСлайд 41 Пирамидальная сортировка Пирамидальная сортировка является улучшенным вариантом сортировки выбором,
в которой на каждом шаге должен определяться наименьший элемент
в необработанном наборе данных. Пирамида определяется как некоторая последовательность ключей K[L], …, K[R], такая, что K[i] K[2i] K[i] K[2i+1], (1)Слайд 42 для всякого i = L, …, R/2. Если
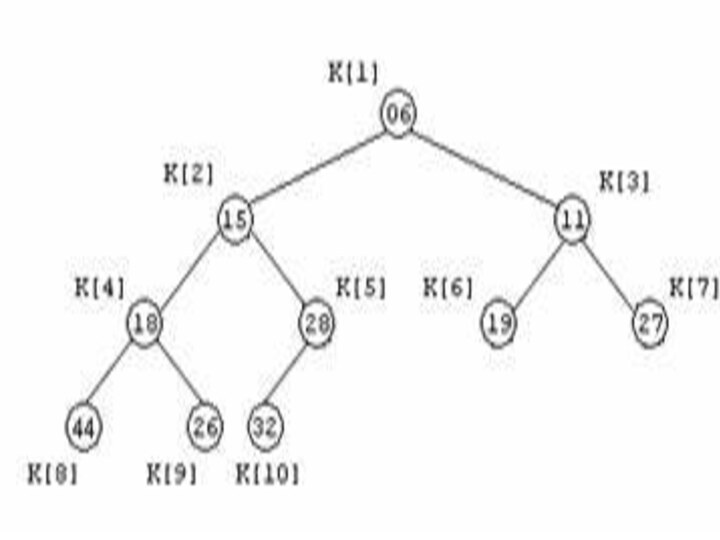
имеется массив K[1], K[2], …, K[R], который индексируется от
1, то этот массив можно представить в виде двоичного дерева. Пример такого представления при R=10 показан на рисунке 1. Рисунок 1 Массив ключей, представленный в виде двоичного дереваСлайд 44 Бинарное (двоичное) дерево (binary tree) - это упорядоченное
дерево, каждая вершина которого имеет не более двух поддеревьев,
причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла.Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом.
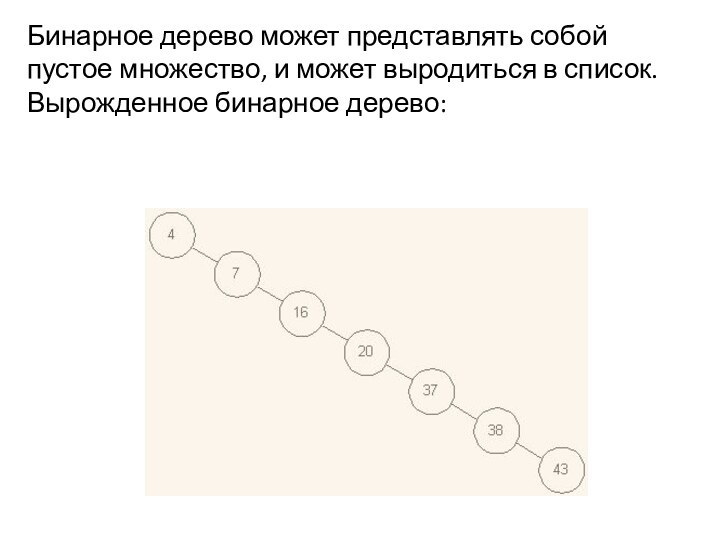
Слайд 46 Бинарное дерево может представлять собой пустое множество, и
может выродиться в список. Вырожденное бинарное дерево:
Слайд 47 Структура для создания корня и узлов дерева имеет
вид: type T = Integer; { скрываем зависимость от конкретного
типа данных } TTree = ^TNode; TNode = record value: T; Left, Right: TTree; end;Слайд 48 Здесь поля Left и Right - это указатели на потомков данного узла,
а поле value предназначено для хранения информации.
При создании дерева вызывается рекурсивная
процедура:procedure Insert(var Root: TTree; X: T);
{ Дополнительная процедура, создающая и инициализирующая новый узел }
procedure CreateNode(var p: TTree; n: T);
begin New(p);
p^.value := n; p^.Left := nil; p^.Right := nil
end;
begin if Root = nil Then
CreateNode(Root, X) { создаем новый узел дерева } else
with Root^ do
begin
if value < X then Insert(Right, X) else
if value > X Then Insert(Left, X) else
{ Действия, производимые в случае повторного внесения элементов в дерево} end; end;
Слайд 49 Эта процедура добавляет элемент X к дереву, учитывая величину X. При
этом создается новый узел дерева.
Слайд 50 Дерево, изображенное на рисунке 2, представляет собой пирамиду,
поскольку для каждого i = 1, 2, …, R/2
выполняется условие (12.1). Очевидно, последовательность элементов с индексами i = R/2+1, R/2+2, …, R (листьев двоичного дерева), является пирамидой, поскольку для этих индексов в пирамиде нет сыновей.Слайд 52 Способ построения пирамиды «на том же месте» был
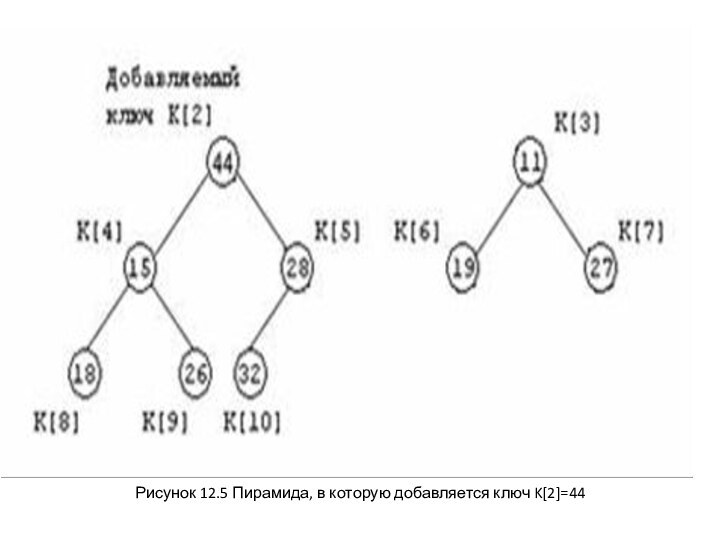
предложен Р. Флойдом. В нем используется процедура просеивания, которую
рассмотрим на следующем примере. Предположим, что дана пирамида с элементами K[3], K[4], …, K[10] нужно добавить новый элемент K[2] для того, чтобы сформировать расширенную пирамиду K[2], K[3], K[4], …, K[10]. Возьмем, например, исходную пирамиду K[3], …, K[10], показанную на рисунке 12.5, и расширим эту пирамиду «влево», добавив элемент K[2]=44.Слайд 53 Добавляемый ключ K[2] просеивается в пирамиду: его значение
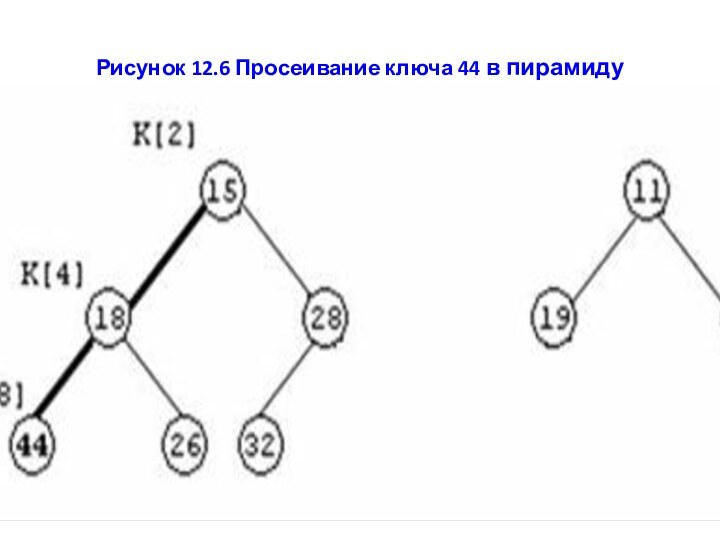
сравнивается с ключами узлов-сыновей, т. е. со значениями 15
и 28. Если бы оба ключа-сына были больше, чем просеиваемый ключ, то последний остался бы на месте, и просеивание было бы завершено. В нашем случае оба ключа‑сына меньше, чем 44, следовательно, вставляемый ключ меняется местами с наименьшим ключом в этой паре, т. е. с ключом 15. Ключ 44 записывается в элемент K[4], а ключ 15 в элемент K[2]. Просеивание продолжается, поскольку ключи-сыновья нового элемента K[4] оказываются меньше его, происходит обмен ключей 44 и 18. В результате получаем новую пирамидуСлайд 54 В нашем примере получалось так, что оба ключа-сына
просеиваемого элемента оказывались меньше его. Это не обязательно: для
инициализации обмена достаточно того, чтобы оказался меньше хотя бы один сыновий ключ, с которым и производится обмен. Просеивание элемента завершается при выполнении любого из двух условий: либо у него не оказывается потомков в пирамиде, либо значение его ключа не превышает значений ключей обоих сыновей.Слайд 56 Достоинства: Имеет доказанную оценку худшего случая O. Требует всего O
дополнительной памяти. Недостатки: Сложен в реализации. Неустойчив — для обеспечения устойчивости нужно
расширять ключ. На почти отсортированных массивах работает столь же долго, как и на хаотических данных. На одном шаге выборку приходится делать хаотично по всей длине массива — поэтому алгоритм плохо сочетается с кэшированием и подкачкой памяти.
Слайд 57
procedure
Sort(var Arr: array of SomeType; Count: Integer);
Procedure
DownHeap(index, Count: integer; Current: SomeType);
//Функция пробегает по
пирамиде восстанавливая ее //Также используется для изначального создания пирамиды //Использование: Передать номер следующего элемента в index //Процедура пробежит по всем потомкам и найдет нужное место для следующего элементаvar
Child: Integer;
Слайд 58
begin
While
index < Count div 2 do
begin
Child := (index+1)*2-1;
if (Child < Count-1) and
(Arr[Child] < Arr[Child+1]) then Child:=Child+1; if Current >= Arr[Child] then break;
Arr[index] := Arr[Child];
index := Child; end;
Arr[index] := Current;
end;
Слайд 59
//Основная функция
var i: integer;
Current: SomeType;
begin
//Собираем пирамиду
for i := (Count div 2)-1 downto
0 do DownHeap(i, Count, Arr[i]); //Пирамида собрана. Теперь сортируем
for i := Count-1 downto 0 do begin Current := Arr[i]; //перемещаем верхушку в начало отсортированного списка
Arr[i] := Arr[0];
DownHeap(0, i, Current); //находим нужное место в пирамиде для нового элемента
end;
end;
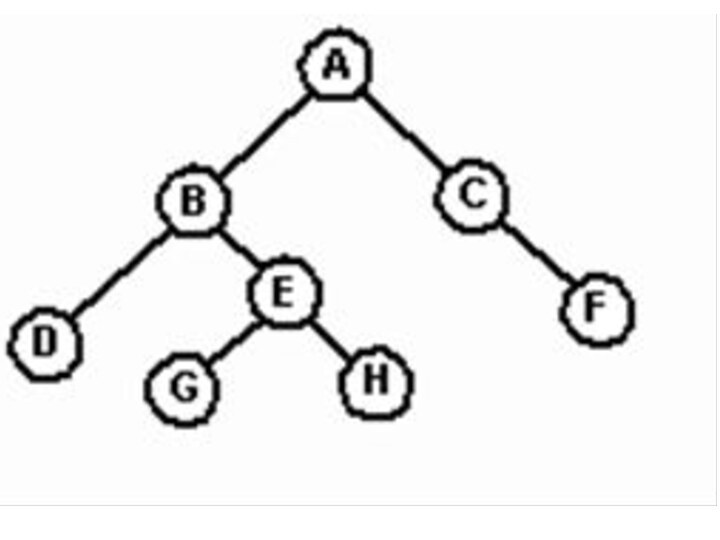
Слайд 61 Это дерево состоит из семи узлов, и А-кореня
дерева. Его левое поддерево имеет корень В, а правое
- корень С. Это изображается двумя ветвями, исходящими из А: левым - к В и правым - к С.Отсутствие ветви обозначает пустое поддерево. Например, левое поддерево бинарного дерева с корнем С и правое поддерево бинарного дерева с корнем Е оба пусты.
Бинарные деревья с корнями D, G, Н и F имеют пустые левые и правые поддеревья.