Слайд 2
Статистика в пед. исследованиях
В.С. Аванесов, Б.П. Битинас, Дж.
Гласс, Жд. Стенли, Л.Б. Ительсон, А.Д. Наследов, Р.С. Немов,
Е.В. Сидоренко, Г.В. Суходольский и др.
«Так как результат психолого-педагогических исследований имеет вероятностный характер, необходимо доказывать статистическую достоверность, значимость полученных результатов».
Слайд 3
Методы статистической обработки –
Математические приёмы, формулы, способы количественных
расчётов, с помощью которых показатели, получаемые в ходе исследования
можно обобщать, систематизировать, выявляя в них скрытые закономерности.
Слайд 4
КЛАССИФИКАЦИЯ МЕТОДОВ СТАТ. ОБРАБОТКИ
Элементарные математические статистики (характеризуют выборочное
распределение данных – выборочное среднее, мода, медиана, выборочная дисперсия
и др.).
Позволяющие судить о динамике изменения (дисперсионный, регрессионный анализ).
Позволяющие судить о связях между переменными величинами (методы сравнения выборочных данных, методы корреляционного, факторного анализа).
Слайд 5
Первичные методы
– с помощью которых можно получить показатели
непосредственно отражающие результаты производимых измерений:
Определение выборочной средней величины
Определение выборочной
дисперсии
Определение выборочной моды
Определение выборочной медианы
Слайд 6
Вторичные методы
- на базе первичных данных выявляют скрытые
в них статистические закономерности:
Корреляционный анализ
Регрессионный анализ
Методы сравнения первичных статистик
двух и более выборок.
Слайд 7
Выборочное среднее значение (среднее арифметическое)
Характеризует степень развития показателя
в целом у группы испытуемых.
Пр. 5, 4, 5, 6,
7 ,3, 6, 2, 9, 4. среднее=5
(сумма частных значений делённая на число показателей)
Слайд 8
Медиана
Середина в выборке (справа и слева одинаковое число
признаков)
Пр. 2,3,4,4,5,6,7,8,9 медиана = 5
0,1,1,2,3,4,5,5,6,7 медиана =3,5
СРЕДНЕЕ ЗНАЧЕНИЕ И
МЕДИАНА ДОЛЖНЫ СОВПАДАТЬ ИЛИ МАЛО ОТЛИЧАТЬСЯ, ТОГДА РАСПРЕДЕЛЕНИЕ СЧИТАЮТ НОРМАЛЬНЫМ!
Слайд 9
Мода и интервал
часто встречающееся значение в выборке
Пр. 1,2,5,2,4,2,6,7,2
мода = 2
Группа упорядоченных по величине значений признаков, заменяемая
в процессе расчётов средним значением
Пр.0,1,1,2,2,3,3,3,4,4,5,5,5,5,6,6,6,7,7,8,8,8,9,9, 9, 10, 10, 11, 11,11.
30 значений разобъём на 6 подрупп по 5 признаков, рассчитаем среднее значение для каждой.
1,2; 3,4; 5,2; 6,8; 8,6;10,6 – интервальный ряд
Слайд 10
Дисперсия
- характеризует насколько частные значения отклоняются от средней
величины в выборке. Чем больше дисперсия, тем больше отклонения,
т.е. разброс данных.
Пр.
1) 5,4,5,6,7,3,6,2,8,4. среднее = 5. Дисперсия = 3
2)5,4,5,6,5,4,5,5,5,6. среднее = 5, Дисперсия = 0,4
Слайд 11
Стандартное отклонение (среднее квадратичное отклонение)
- квадратный корень из
дисперсии, служит для вычисления разброса частных данных относительно средней.
Слайд 12
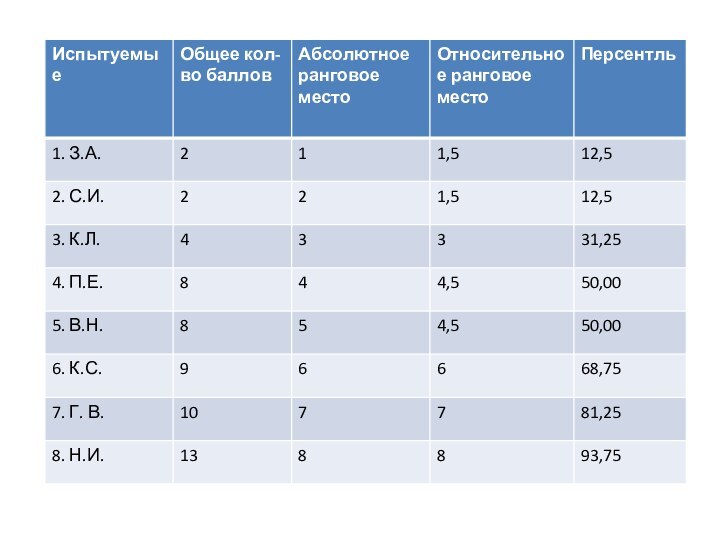
Персентль
Процентный ранговый показатель РR, в порядковых измерениях.
PR=2R-1/2N ×100,
где R – относительное ранговое место испытуемого, N –
количество членов группы.
Пр. Для З.А по данным таблицы (след. слайд).PR= 2 ×1,5 – 1)/16 × 100 = 12,50
Слайд 14
Вторичные методы применяются только для нормальной выборки!
Если выборочное
распределение признаков нормально, то к нему можно применять методы
вторичных статистических расчётов, которые основаны на нормальном распределении данных. Иначе могут быть ошибки!!!
Слайд 15
Вторичные методы стат. обработки
Служат для подтверждения или опровержения
статистических гипотез (предположений относительно сходства или различия функциональных или
числовых характеристик случайных явлений).
Нулевая гипотеза (Н о) – противоположная (альтернативная) гипотеза (Н 1)
Слайд 16
Гипотезы исследования
Направленные
Пр. Но: Х1 не превышает Х2,
тогда Н1: Х1 превышает Х2
Ненаправленные
Пр. Но: Х1 не отличается
Х2, тогда Н1: Х1 отличается Х2
Слайд 17
Статистический критерий
- некоторая случайная величина, представляющая собой какой-либо
функционал от значений сравниваемых функциональных или числовых характеристик.
Параметрические –
включают в формулу расчёта параметры распределения, т. е средние и дисперсии (Стьюдента, Фишера и др.)
Непараметрические - основаны на оперировании частотами или рангами(Пирсона, Вилкоксона и др.)
Слайд 18
Допустимые уровни значимости
0,1
0,05
0,01
Слайд 19
Сопоставление основных моделей ПЭ и статистических методов
Слайд 20
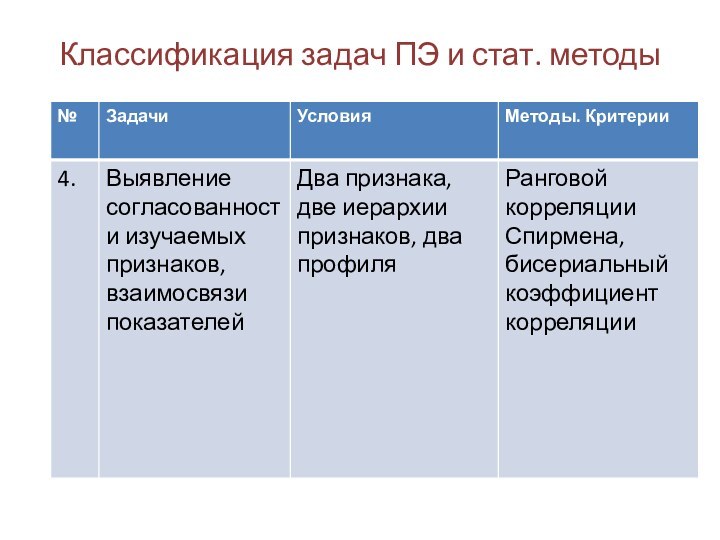
Классификация задач ПЭ и стат. методы
Слайд 21
Классификация задач ПЭ и стат. методы
Слайд 22
Классификация задач ПЭ и стат. методы
Слайд 23
Классификация задач ПЭ и стат. методы
Слайд 24
Классификация задач ПЭ и стат. методы
Слайд 25
Классификация задач ПЭ и стат. методы