Слайд 2
Классификации в статистической практике
Признак, имеющий качественно отличную характеристику
и служащий основой для разграничения элементов в совокупности на
группы называется группировочным признаком
Группировочным признаком может быть любой признак (атрибутивный или количественный). В зависимости от сложности явления и цели исследования группировочных признаков может быть несколько.
Слайд 3
Если разграничение элементов совокупности на группы осуществляется по
атрибутивным (качественным) признакам, то такой вид группировки называют классификацией
или номенклатурой.
Классификации или номенклатуры разрабатываются международными и национальными статистическими органами и рекомендуются как статистический стандарт.
Слайд 4
Классификатор, где каждому значению группровочного признака присвоен код,
то есть условное цифровое обозначение.
Слайд 5
Российская Федерация использует такие основные виды классификаторов.
■ Общероссийский
классификатор видов экономической деятельности, продукции и услуг (ОКДП), который
включает 55 тысяч видов продукции и услуг по 6 уровням классификации (раздел, подраздел, группа, подгруппа, класс, подкласс);
■ Общероссийский классификатор продукции (ОКП), предназначенный для автоматизированной обработки информации на национальном, региональном и отраслевом уровнях; содержит около 50 тыс. видов продукции по такой иерархии; класс, подкласс, группа, подгруппа, вид.
Слайд 6
■ Общероссийский классификатор форм собственности (ОКФС), дающий возможность
установить распределение предприятий по формам собственности (российская собственность, иностранная
собственность, совместная российская и иностранная собственность);
■ Общероссийский классификатор организационно-правовых форм (ОКОПФ), который включает разделы: юридические лица для коммерческих и некоммерческих организаций; организации без права юридического лица: индивидуальные лица; индивидуальные предприниматели.
Слайд 7
Группировка статистических данных
Если разграничение элементов совокупности на группы
осуществляется по количественным признакам, то такой вид группировки называют
статистической группировкой
Слайд 8
Типы группировок
В зависимости от цели и заданий исследования
различают такие виды группировки:
типологические;
структурные;
аналитические.
Слайд 9
Типологическими группировками, называют такие группировки, которые приводят к
выделению в составе массовых явлений их социально-экономических типов (то
есть однородных частей по качеству и условиям развития, в которых действуют одни и те же закономерности).
Слайд 10
Структурные группировки характеризуют состав однородной совокупности по любым
признакам.
С помощью таких группировок анализируют структуру совокупности и
структурные сдвиги в развитии социально-экономических явлений и процессов. К ним принадлежат группировки населения по полу, возрасту, а на производстве — группировка рабочих по производственному стажу, уровню квалификации и др.
Слайд 11
Группировки, которые направлены на выявление связи между отдельными
признаками изучаемого явления, называются аналитическими.
Примерами таких группировок могут
быть группировки, в которых изучаются взаимосвязи между себестоимостью и ее факторами, производительностью труда и ее факторами и т. п.
Слайд 12
По количеству группировочных признаков, положенных в основу группировки,
различают:
простые группировки;
комбинированные группировки.
Слайд 13
простой называют группировку, которая проводится по одному признаку.
Комбинированной называют группировку при сочетании двух и больше группировочных
признаков.
Слайд 14
При использовании метода группировки решают такие задачи:
а) выбор
группировочного признака;
б) определение количества групп и величины интервала;
в) установление
перечня показателей, которыми должны характеризоваться выделенные группы относительно конкретной группировки;
г) составление макетов таблиц, где будут представлены результаты группировки;
д) вычисление абсолютных, относительных и средних показателей;
ж) табличное и графическое оформление результатов группировки.
Слайд 15
Принципиальное значение при построении группировок имеет выбор группировочного
признака, на основе которого выделяют разные типы, группы и
подгруппы.
В качестве группировочного принимают наиболее существенные признаки.
Группировочным признаком может быть атрибутивный (качественный) или количественный признак.
Слайд 16
Если группировка осуществляется по атрибутивному признаку, то выделяют
столько групп, сколько имеется наименований признака.
Слайд 17
Пример группировки по атрибутивному признаку
Рассмотрим распределение городских земельных
площадей по виду застройки (атрибутивным признакам)
Слайд 18
Такой вид группировки относится к структурной, которая в
этом примере характеризует масштабы и весомость отдельных видов застройки
на территории города.
Слайд 19
При составлении группировок на основе количественных признаков (дискретных
или непрерывных) определяют количество групп и интервалы группировки.
В массовой
совокупности оптимальное количество групп с равными интервалами приблизительно можно определить по формуле американского ученого Стерджеса:
т=1+3,322lgn,
где т - количество групп; п - объем совокупности.
Слайд 20
Формула Стерджеса может быть использована при условии, что
распределение единиц совокупности за данным признаком приближается к нормальному
закону распределения.
Интервалы, то есть промежуток между значениями признака в группе единиц, бывают равные, неравные, открытые и закрытые. Выбор вида интервала зависит от характера распределения единиц исследуемой совокупности.
Слайд 21
Равные интервалы используют в случаях, когда значения варьируемого
признака х изменяются плавно, постепенно, равномерно. Ширина интервала h
определяется по формуле:
где - наибольшее и наименьшее значение признака в совокупности.
Слайд 22
Пример
Прибыльность активов коммерческих банков колеблется в пределах от
5 к 45%.
При принятии количества групп т=4 ширина
интервала - 10. Тогда границы интервалов составляются соответственно:
5-15, 15-25, 25-35, 35-45.
Слайд 23
Поскольку границы интервалов совпадают (15 - в первой
и второй группе, 25 - во второй и третьей,
35 - в третьей и четвертой), то для исключения неопределенности отнесения граничных значений признака к той или другой группе используют следующее правило:
Слайд 24
Правило
левое одинаковое число не включает в себя значения
признака, правое - включает.
Слайд 25
Тогда, например, число 15 должно быть отнесено ко
второй группе, а не к первой. Все интервалы в
данном примере называются закрытыми.
Слайд 26
Приведенное распределение прибыльности активов банков может быть представлено
в другом виде:
до 15. 15-25, 25-35, 35 и
более.
Первый и последний интервалы имеют лишь одну границу и называются открытыми
Слайд 27
Неравные интервалы используются в случае, когда диапазон значений
признака слишком широкий и распределение совокупности по этому признаку
неравномерно.
Пример
Рассмотрим распределение поселков городского типа по количеству жителей (тыс. чел.):
до 3; 3-4,9; 5-9,9; 10-49,9.
Слайд 28
Ряды распределения
Особый вид группировок в статистике представляют ряды
распределения, которые являются самым простым способом обобщения статистических данных.
Рядом распределения называют группировку, характеризующую состав (структуру) явления в данный период времени.
Слайд 29
В зависимости от того, какой признак (качественный или
количественный) положен в основу группировки различают:
атрибутивные (качественными) ряды
распределения
вариационные (количественными) ряды распределения .
Слайд 30
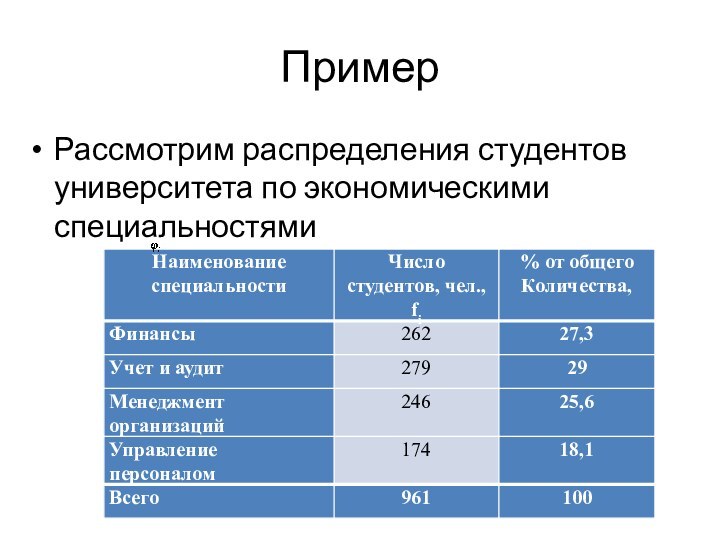
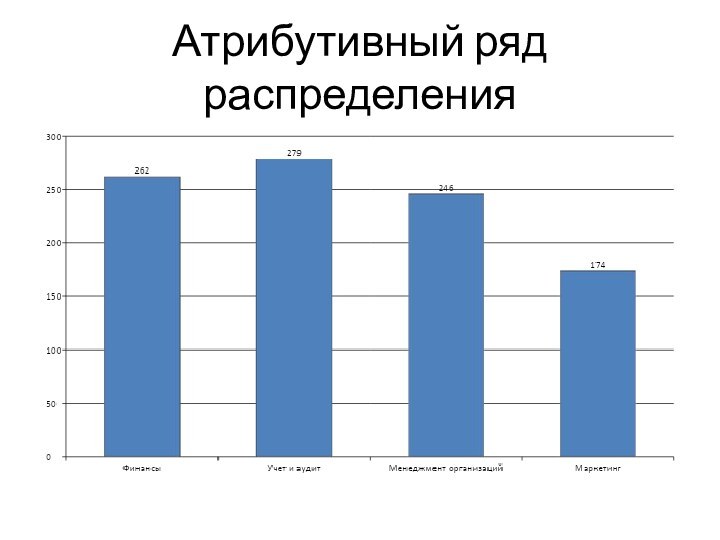
Пример
Рассмотрим распределения студентов университета по экономическими специальностями
Слайд 32
Элементами (характеристиками) этого ряда распределения являются:
значения атрибутивного
признака (первая графа таблицы);
частоты fi - численные характеристики
отдельных значений признака, то есть числа, которые показывают, как часто встречается то или другое значение признака в ряду (вторая графа);
Слайд 33
частости - это частоты,
выраженные в относительных величинах (коэффициентах или процентах), что приведено
в третьей графе таблицы.
Слайд 34
Вариационные ряды распределения бывают
дискретными
интервальными.
Дискретные вариационные ряды основаны
на величинах признаков, которые имеют целые значения (например, тарифный
разряд рабочих, количество марок автомобилей и т. п.).
Слайд 35
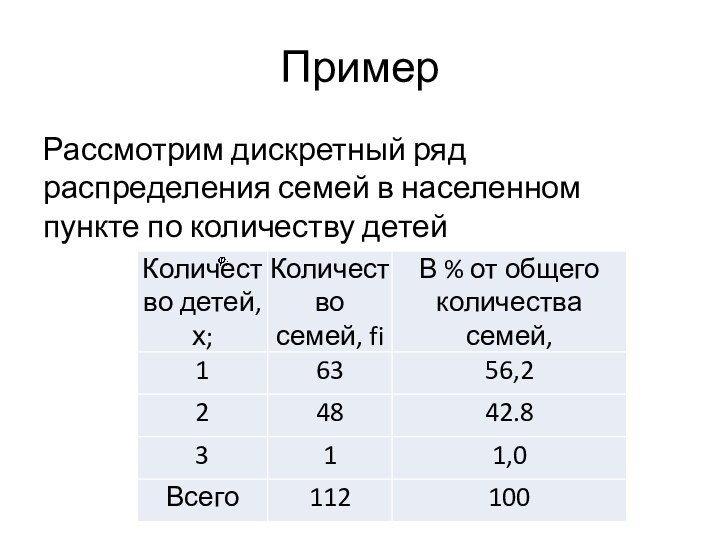
Пример
Рассмотрим дискретный ряд распределения семей в населенном пункте
по количеству детей
Слайд 36
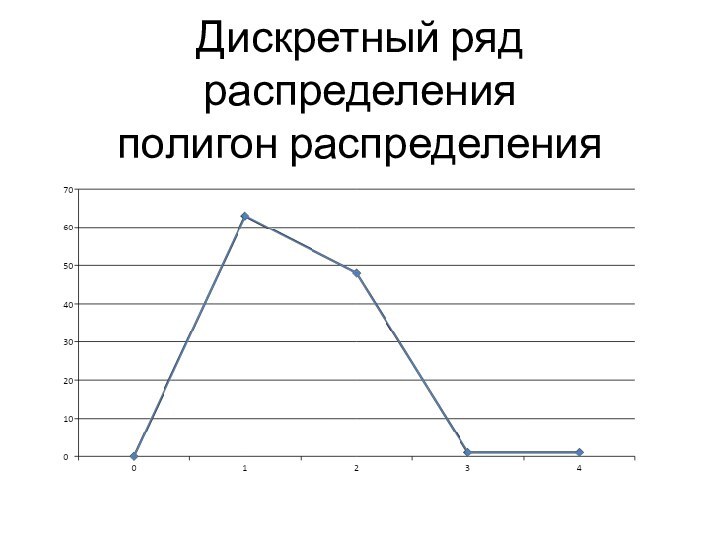
Дискретный ряд распределения
полигон распределения
Слайд 37
К основным элементам вариационных рядов распределения относятся:
варианты
х. — численные значения количественного признака в группировке (первая
графа таблиц), которые могут быть положительными, отрицательными, абсолютными, относительными;
частоты fi — значение отдельных вариант (вторая графа);
частости (третья графа).
Слайд 38
В интервальных вариационных рядах группировочный признак может принимать
любое значение (целое, дробное) в пределах каждого интервала (например,
распределение заработной платы работающих в организации, распределение основных фондов предприятия и т. п.).
Слайд 39
Пример
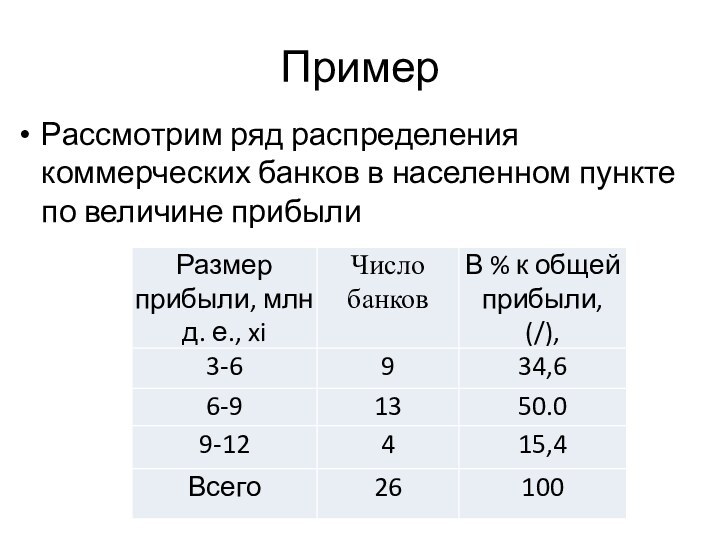
Рассмотрим ряд распределения коммерческих банков в населенном пункте
по величине прибыли
Слайд 40
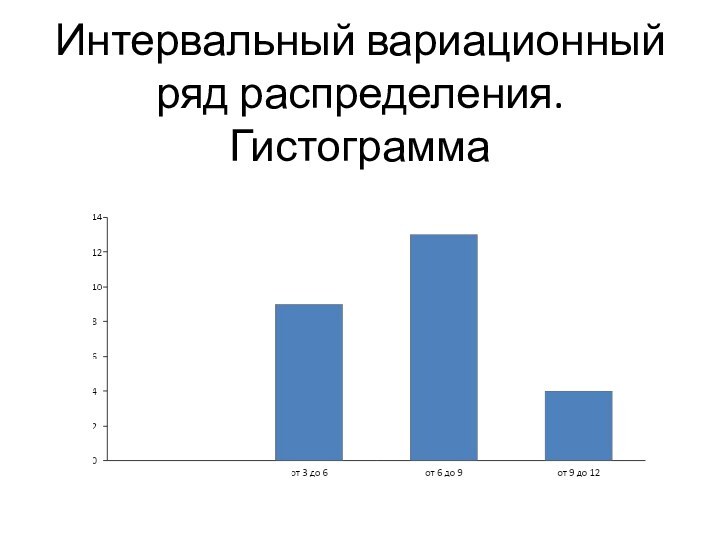
Интервальный вариационный ряд распределения. Гистограмма
Слайд 41
Кроме отмеченных элементов вариационных рядов к их характеристикам
могут быть отнесены также такие показатели-
- плотность частоты
где h - ширина интервала;
накопленная частость .
Такие показатели используются при анализе построенных рядов распределения.
Слайд 42
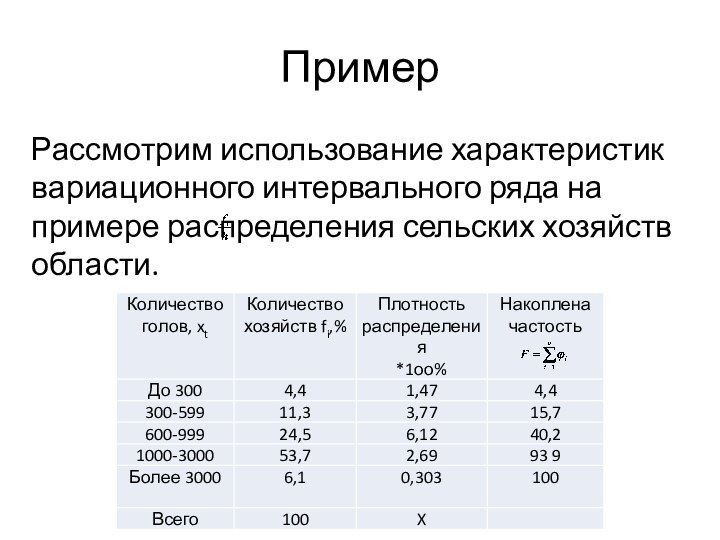
Пример
Рассмотрим использование характеристик вариационного интервального ряда на примере
распределения сельских хозяйств области.
Слайд 43
Статистические таблицы
Таблица по своему логическому содержанию рассматривается как
«статистическое предложение», которое имеет свое подлежащее и сказуемое.
Подлежащее
таблицы характеризует объект исследования.
Сказуемое — это система показателей, которые отображают подлежащее как объект.
Слайд 44
В зависимости от структуры подлежащего статистические таблицы разделяют
на
простые,
групповые,
комбинированные.
Подлежащее простой таблицы представляет собой перечень единиц
явления или процесса. В сказуемом простой таблицы отсутствует группировка статистических данных. Такие таблицы могут быть перечневыми, хронологическими, территориальными.
Слайд 45
Пример простой перечневой таблицы
Наличие строительных машин в
строительных управлениях региона по состоянию на в 01.01.2013 года
Слайд 46
Подлежащим таблицы является вид машин, сказуемым - количество
разных их видов.
Слайд 47
В групповых статистических таблицах подлежащее группируется по одному
признаку, а у комбинированных - по двум и больше
признакам
Слайд 48
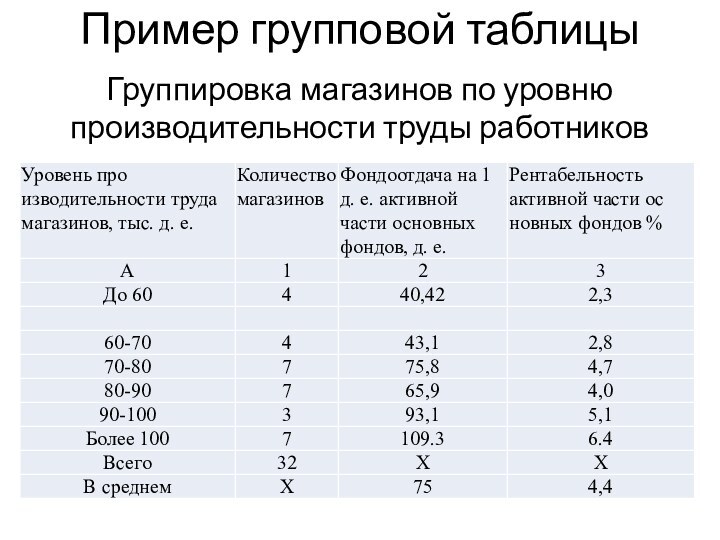
Пример групповой таблицы
Группировка магазинов по уровню производительности труды
работников
Слайд 49
В приведенной групповой таблице подлежащим являются магазины города,
которые разделены на группы по уровню производительности труда, сказуемым
- показатели этих организаций (количество магазинов, фондоотдача, рентабельность).
Слайд 50
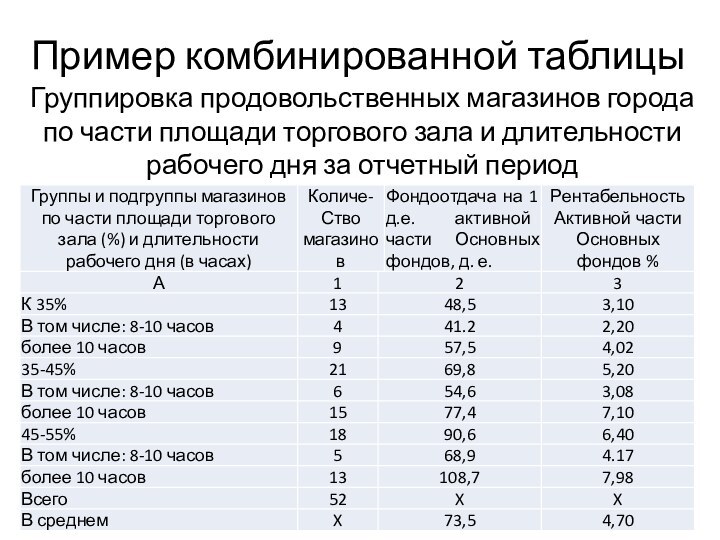
Пример комбинированной таблицы
Группировка продовольственных магазинов города по
части площади торгового зала и длительности рабочего дня за
отчетный период
Слайд 51
Подлежащим данной таблицы являются магазины, распределенные на группы
и подгруппы по части площади торгового зала и длительности
рабочего дня; в сказуемом приведены показатели, которые наиболее полно характеризуют эффективность работы магазинов.
Слайд 52
Макет таблицы - это комбинация горизонтальных строк и
вертикальных граф (столбцов), на пересечении которых образуются клетки для
записи соответствующей информации. Левые боковые и верхние клетки предназначены для словесных заглавий подлежащего и системы показателей сказуемого. Другие клетки таблицы предусмотрены для численных статистических данных. Основное содержание таблицы указывается в ее названии.
Слайд 53
Технические правила составления таблиц
1. Название таблицы, заглавия строк
и граф должны быть четкими, лаконичными, без сокращений, лишней
и второстепенной информации.
2. В названии таблицы указывается ее порядковый номер, объект исследования, его временной и географический признак. Если названия отдельных граф или строк повторяются, то их целесообразно объединить общим заглавием.
Слайд 54
3. В верхних и боковых заглавиях указываются единицы
измерения с использованием общепринятых сокращений (руб., т, м и
т. п.). Если единица измерения общая для всех данных таблицы, ее указывают в названии таблицы.
4. Для сложных в построении таблиц графы целесообразно нумеровать: графу с названием подлежащего помечают литерой алфавита, а другие графы — цифрами.
Слайд 55
5. Обобщенная информация граф таблицы содержится в итоговой
строке с отметкой «Итого» (промежуточный итог) «Всего» (окончательный итог),
«В среднем».
6. Значение показателей в клетках таблицы следует округлять в границах одной строки или графы с одинаковой степенью точности (до целых; 0,1; 0,01 и т. д.).