- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Безу. Схема Горнера и её применение
Содержание
- 2. Содержание Вывод формул для
- 3. Горнер Уильям Джордж (1786 - 1837) Английский
- 4. Вывод формул для схемы ГорнераРазделить с остатком
- 5. Демонстрация работы схемы ГорнераС помощью схемы Горнера
- 6. Разложение многочлена по степеням двучленаИспользуя схему Горнера,
- 7. Домашняя работаРазделить f(x)=2x5-x4-3x3+x-3 на x-3;Используя схему Горнера,
- 8. Скачать презентацию
- 9. Похожие презентации
Содержание Вывод формул для схемы ГорнераДемонстрация работы схемы ГорнераРазложение многочлена по степеням двучленаДомашняя работа







Слайд 2
Содержание
Вывод формул для схемы Горнера
Демонстрация работы схемы Горнера
Разложение
многочлена по степеням двучлена
Слайд 3
Горнер Уильям Джордж (1786 - 1837)
Английский математик.
Основные исследования относятся к теории алгебраических уравнений. Разработал способ
приближенного решения уравнений любой степени. В 1819 г. ввёл важный для алгебры способ деления многочлена на двучлен (х – а) (схема Горнера).
Слайд 4
Вывод формул для схемы Горнера
Разделить с остатком многочлен
f(x) на двучлен (x-c) значит найти такой многочлен q(x)
и такое число r, что f(x)=(x-c)q(x)+rЗапишем это равенство подробно:
f0 xn + f1 xn-1 + f2 xn-2 + …+fn-1 x + fn =
=(x-c) (q0 xn-1 + q1 xn-2 + q2 xn-3 +…+ qn-2 x + qn-1 )+r
Приравняем коэффициенты при одинаковых степенях:
xn : f0 = q0 => q0 = f0
xn-1 : f1 = q1 - c q0 => q1 = f1 + c q0
xn-2 : f2 = q2 - c q1 => q2 = f2 + c q1
… …
X0 : fn = qn - c q n-1 => qn = fn + c qn-1
Слайд 5
Демонстрация работы схемы Горнера
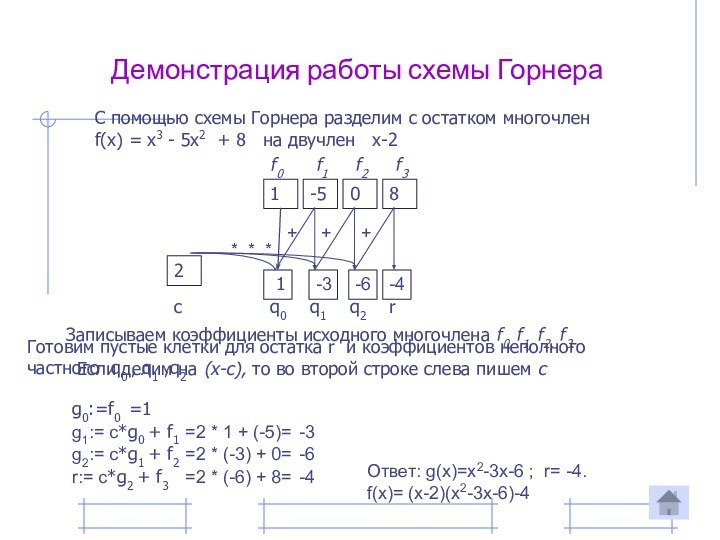
С помощью схемы Горнера разделим
с остатком многочлен f(x) = x3 - 5x2 +
8 на двучлен x-2Записываем коэффициенты исходного многочлена f0, f1, f2, f3.
f0
f1
f2
f3
1
-5
0
8
c
2
Если делим на (x-c), то во второй строке слева пишем с
Готовим пустые клетки для остатка r и коэффициентов неполного
частного q0 , q1 ,q2
q0
q1
q2
r
g0:=f0
=1
1
g1:= с*g0 + f1
*
+
=2 * 1 + (-5)=
-3
-3
g2:= с*g1 + f2
=2 * (-3) + 0=
-6
*
+
-6
r:= с*g2 + f3
=2 * (-6) + 8=
*
+
-4
-4
Ответ: g(x)=x2-3x-6 ; r= -4.
f(x)= (x-2)(x2-3x-6)-4
Слайд 6
Разложение многочлена по степеням двучлена
Используя схему Горнера, разложим
многочлен f(x)=x3+3x2-2x+4 по степеням двучлена (x+2)
1
3
4
-2
-2
1
-4
12
1
-2
f(x)=x3+3x2-2x+4 =(x+2)(x2+x-4)+12
1
-2
-1
f(x)=x3+3x2-2x+4= (x+2)((x-1)(x+2)-2)+12
-2
1
-3
f(x)=x3+3x2-2x+4=
(((1*(x+2)-3)(x+2)-2)(x+2))+12-2
1
f(x) = x3+3x2-2x+4 = (x+2)(x2+x-4)+12 = (x+2)((x-1)(x+2)-2)+12 =
= (((1*(x+2)-3)(x+2)-2)(x+2))+12 = (x+2)3 -3(x+2)2 -2(x+2)+12