- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теоремы об углах, образованных хордами, касательными и секущими
Содержание
- 2. Угол между пересекающимися хордамиВеличина угла, образованного пересекающимися
- 3. ДоказательствоПоскольку угол AED – внешний угол треугольника
- 4. Угол, образованный секущими, которые пересекаются вне кругаВеличина
- 5. ДоказательствоПоскольку угол ADC – внешний угол треугольника
- 6. Угол, образованный касательной и секущейВеличина угла, образованного
- 7. Доказательство
- 8. Угол, образованный касательной и хордой, проходящей через
- 9. Доказательство1) Поскольку AD – диаметр, проходящий через
- 10. решение задач
- 11. ЗадачаОкружность проходит через вершины A и B
- 12. Решение1)Пусть D — точка пересечения данной окружности с прямой BC.
- 13. ЗадачаДве окружности касаются друг друга внутренним образом
- 14. РешениеДокажем сначала, что точка M — середина
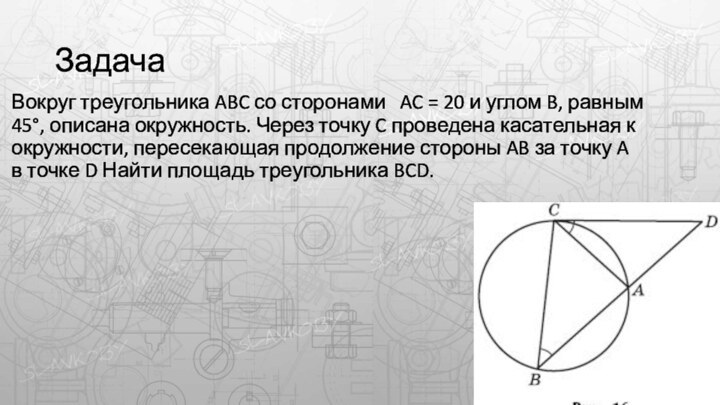
- 15. ЗадачаВокруг треугольника ABC со сторонами AC
- 16. РешениеУгол ABC равен половине угловой величины дуги
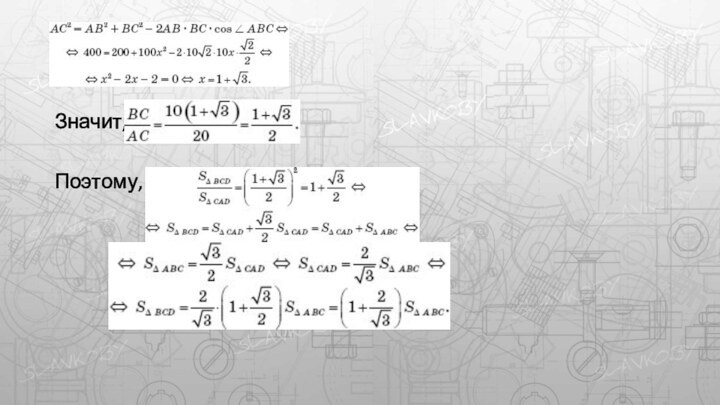
- 17. Значит, Поэтому,
- 18. С другой стороныЗначит
- 19. Скачать презентацию
- 20. Похожие презентации














Слайд 2
Угол между пересекающимися хордами
Величина угла, образованного пересекающимися хордами,
равна половине суммы величин дуг, заключённых между его сторонами
Слайд 3
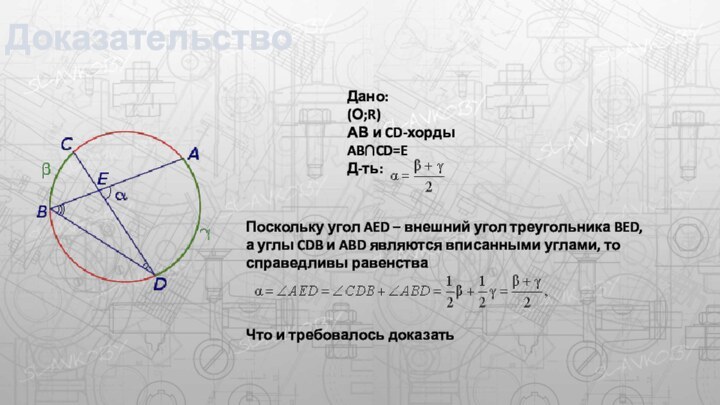
Доказательство
Поскольку угол AED – внешний угол треугольника BED,
а углы CDB и ABD являются вписанными углами, то
справедливы равенстваЧто и требовалось доказать
Дано:
(О;R)
АВ и CD-хорды
AB∩CD=E
Д-ть:
Слайд 4
Угол, образованный секущими, которые пересекаются вне круга
Величина угла,
образованного секущими, пересекающимися вне круга, равна половине разности величин
дуг, заключённых между его сторонами
Слайд 5
Доказательство
Поскольку угол ADC – внешний угол треугольника ADE,
а углы ADC , DCB и DAB являются вписанными
углами, то справедливы равенствачто и требовалось доказать.
Дано:
(O;R)
AB и CD секущие
AB∩CD=E
Д-ть:
Слайд 6
Угол, образованный касательной и секущей
Величина угла, образованного касательной
и секущей, равна половине разности величин дуг, заключённых между
его сторонами
Слайд 7
Доказательство
=>
Поэтому справедливы равенствачто и требовалось доказать.
Дано:
(O;R)
CD-сек
AB∩CD=E
Д-ть:
Слайд 8 Угол, образованный касательной и хордой, проходящей через точку
касания
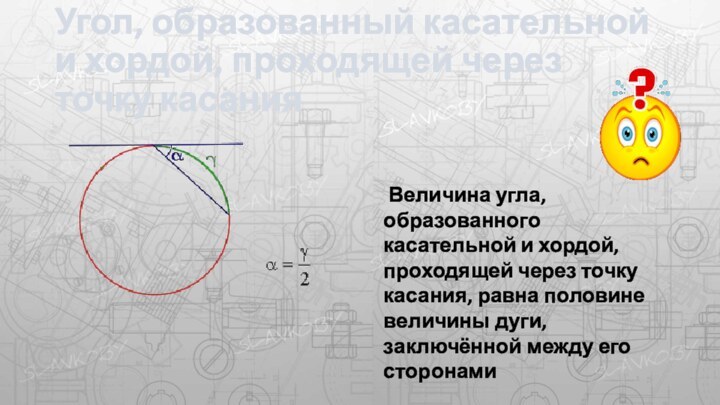
Величина угла, образованного касательной и хордой, проходящей через
точку касания, равна половине величины дуги, заключённой между его сторонами
Слайд 9
Доказательство
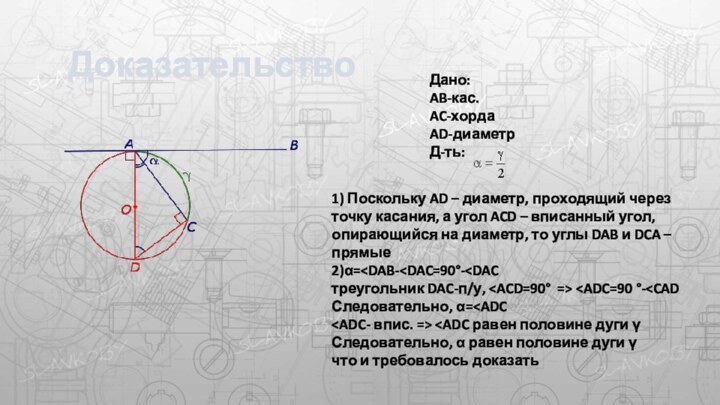
1) Поскольку AD – диаметр, проходящий через точку
касания, а угол ACD – вписанный угол, опирающийся на
диаметр, то углы DAB и DCA – прямые2)α=
что и требовалось доказать
Дано:
AB-кас.
AC-хорда
AD-диаметр
Д-ть:
Слайд 11
Задача
Окружность проходит через вершины A и B треугольника
ABC и касается прямой AC в точке A. Найдите
радиус окружности, если угол BAC = α, угол ABC = β и площадь треугольника ABC равна S.Подсказка
Пусть D — точка пересечения данной окружности со стороной BC. Зная площадь треугольника ABC,
найдите AB с помощью теоремы синусов.
Затем докажите, что ADB = 180o -
Слайд 12
Решение
1)Пусть D — точка пересечения данной окружности с прямой BC. Обозначим AB = c, BC = a.
Применяя теорему синусов к треугольнику ABC, получим пропорцию
=
= ,откуда a = .
Тогда
S = S ABC = ac sin = ,
откуда находим, что c =
2) По теореме об угле между касательной и хордой находим, что либо ADB = BAC = , либо ADB = 180o - BAC = 180o - В обоих случаях sin ADB = sin . Пусть R — искомый радиус окружности, описанной около треугольника ABD.
Тогда
R = = = .
Слайд 13
Задача
Две окружности касаются друг друга внутренним образом в
точке A. Хорда BC в большей окружности касается меньшей
в точке D. Прямая AD вторично пересекает большую окружность в точке M. Найдите MB, если MA = a, MD = b.
Слайд 14
Решение
Докажем сначала, что точка M — середина дуги
BC, не содержащей точки A. Пусть общая касательная к
данным окружностям, проведённая через точку A, пересекает прямую BC в точке P (C между B и P). Тогда ∠MAP = ∠ADP как углы при основании равнобедренного треугольника APD.Пусть α, β и γ — угловые величины дуг CM (не содержащей точки A), BM (не содержащей точки A) и AB (не содержащей точки C) соответственно. Тогда из равенства углов MAP и ADP следует равенство смежных им углов, поэтому
α + γ
2 ,
γ + β
2
=
______ ______
откуда получаем, что α = β. Значит,
∠DBM = ∠CBM = ∠CAM = ∠BAM
и треугольники BDM и ABM подобны по двум углам. Следовательно,
BM
DM
откуда находим, что BM² = AM · DM = ab.
=
AM
BM
,
____ ____