Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Тригонометрическиефункции

Содержание

2. ПланФункция у = sinx, ее исследование и
3. Функция у = sinxФункция у = sinx
4. Нечетность функции у = sinxsin(−х) = − sin х;
5. Периодические функцииПосмотрим на единичную окружность
6. sin(x + 2πn) = sin(x). Число 2πn также период функции. Число 2π – наименьший положительный период.
7. Максимальное и
8. График функции y = sinx
9. Функция у = cosxФункция у = cosx
10. Четность функции у = cosxcos(−х) = cosх;
11. Периодичность у = cosхПосмотрим на
12. cos(x + 2πn) = cos (x). Число
13. Максимальное и
14. График функции y = cosxcos(x)
15. Функции тангенс и котангенсЧисловые функции, заданные равенствами
16. Множество значений тангенса и котангенса – вся
17. Линия тангенсовПрямая ОР проходит через начало координат
18. ВыводЧтобы найти значение тангенса для конкретного аргумента
19. Табличные значения tg 0
20. Табличные значения tg() =
21. График функции y = tgx
22. Линия котангенсов
23. Табличные значенияctg 0
24. Период функции y = ctgxПериод
25. График котангенса
26. Функции секонс и косеконсФункция у = 1/cosx
27. Шесть тригонометрических функцийsinx, cosx, tgx, ctgx, secx,
28. Домашнее заданиеЗапомнить, какие функции нечетные, какие –
29. Скачать презентацию
30. Похожие презентации

ПланФункция у = sinx, ее исследование и графикФункция y = cosx, ее исследование и графикФункции тангенс и котангенс, их исследование и графикиФункции секонс и косеконс, определение

Главная
Разное
Тригонометрическиефункции

Тригонометрические функции Автор Календарева Н.Е.© 2011 г.

ПланФункция у = sinx, ее исследование и графикФункция y = cosx, ее

Функция у = sinxФункция у = sinx определена на всей числовой прямой.Def(sinx)

Нечетность функции у = sinxsin(−х) = − sin х;

Периодические функцииПосмотрим на единичную окружность и заметим, что sin( x

sin(x + 2πn) = sin(x). Число 2πn также период функции. Число 2π – наименьший положительный период.

Максимальное и минимальное значенияФункция

Функция у = cosxФункция у = cosx определена на всей числовой прямой.Def(cosx)

Четность функции у = cosxcos(−х) = cosх;

Периодичность у = cosхПосмотрим на единичную окружность и заметим, что

cos(x + 2πn) = cos (x). Число 2πn также период функции. Число

График функции y = cosxcos(x) = sin(2 + x) или

Функции тангенс и котангенсЧисловые функции, заданные равенствами у = tg x и

Множество значений тангенса и котангенса – вся числовая прямая, т.е. R. Тангенс

Линия тангенсовПрямая ОР проходит через начало координат и точку Р(cosα ; sinα).

ВыводЧтобы найти значение тангенса для конкретного аргумента х, надо изобразить линию тангенсов,

Табличные значения tg() = 1; tg(6) =

Табличные значенияctg 0 не существует. ctg ()

Период функции y = ctgxПериод функции равен k, где k

Функции секонс и косеконсФункция у = 1/cosx называется секонсом:y = 1/cosx =

Шесть тригонометрических функцийsinx, cosx, tgx, ctgx, secx, cosecxПравило, как запомнить:sinx ∙ cosecx

Домашнее заданиеЗапомнить, какие функции нечетные, какие – четныеЗапомнить графики синуса, косинуса и

Слайды презентации

Слайд 2 План
Функция у = sinx, ее исследование и график
Функция

ПланФункция у = sinx, ее исследование и графикФункция y = cosx,

y = cosx, ее исследование и график
Функции тангенс и

котангенс, их исследование и графики
Функции секонс и косеконс, определение

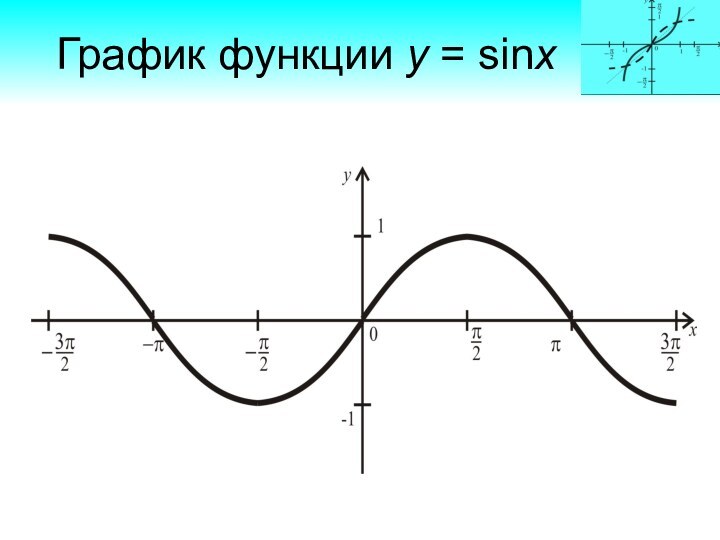
Слайд 3 Функция у = sinx
Функция у = sinx определена

Функция у = sinxФункция у = sinx определена на всей числовой

на всей числовой прямой.
Def(sinx) = (– ∞; + ∞);
E(sinx)

= [–1; 1].
Так как О.О. симметрична относительно 0, то проверим равенство
sin(–x) = –sinx.
Функция нечетная. В самом деле.

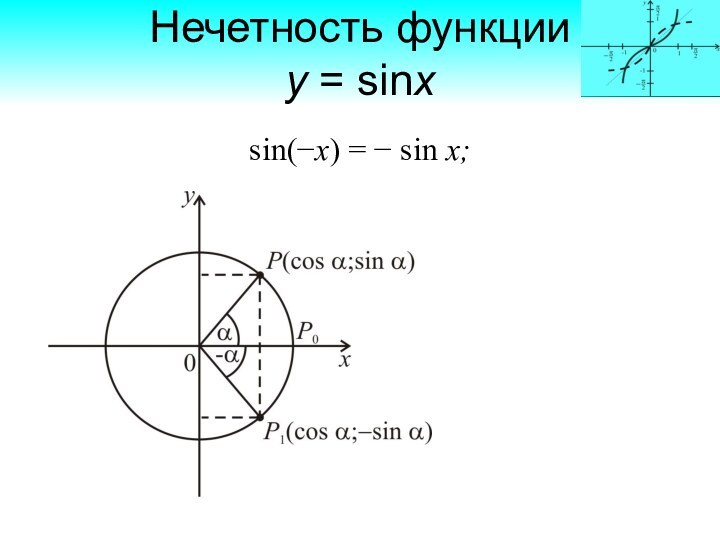
Слайд 4 Нечетность функции у = sinx
sin(−х) = − sin

х;

Слайд 5 Периодические функции
Посмотрим на единичную окружность и

заметим, что sin( x + 2π) = sin( x).
Аналогично

sin( x − 2π) = sin( x). О таких функциях говорят, что они периодические с периодом 2π. Если сделать несколько оборотов, например 2π∙n, где n є Z, то значения функции синуса не изменится:

Слайд 6 sin(x + 2πn) = sin(x). Число 2πn также

период функции. Число 2π – наименьший положительный период.

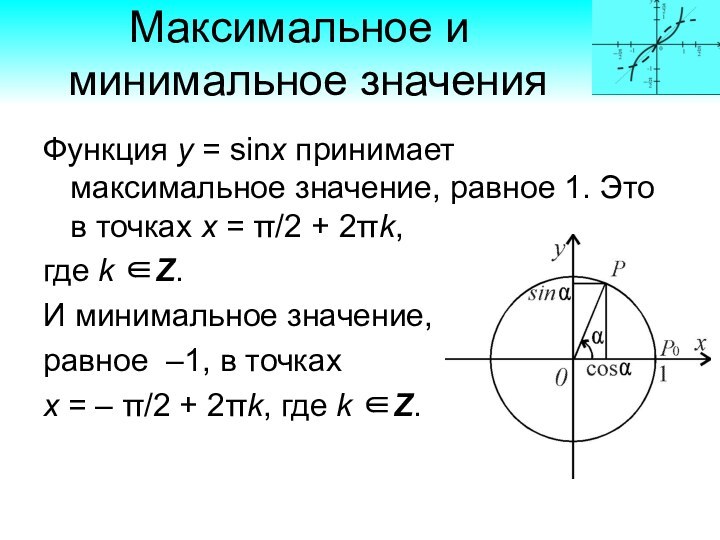
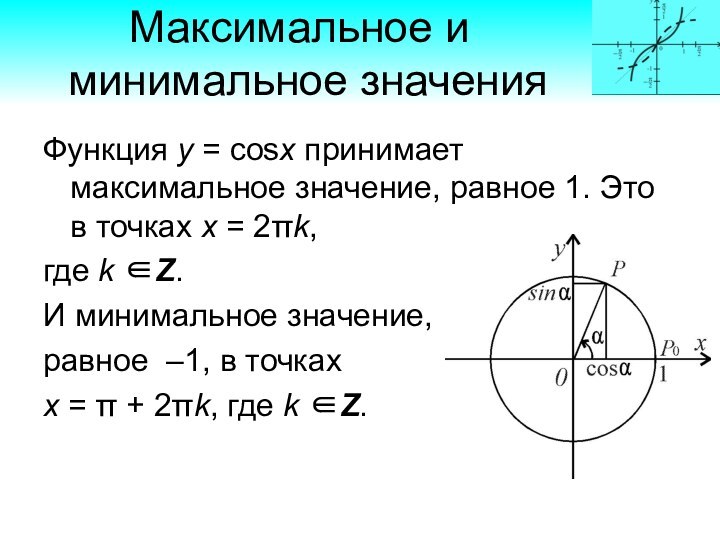
Слайд 7 Максимальное и

Максимальное и минимальное значенияФункция у = sinx

минимальное значения
Функция у = sinx принимает максимальное значение,

равное 1. Это в точках х = /2 + 2k,
где k .
И минимальное значение,
равное –1, в точках
х = – /2 + 2k, где k .

Слайд 8 График функции y = sinx

Слайд 9 Функция у = cosx
Функция у = cosx определена

Функция у = cosxФункция у = cosx определена на всей числовой

на всей числовой прямой.
Def(cosx) = (– ∞; + ∞);
E(cosx)

= [–1; 1].
Так как О.О. симметрична относительно 0, то проверим равенство
cos (–x) = cosx.
Функция четная. В самом деле.

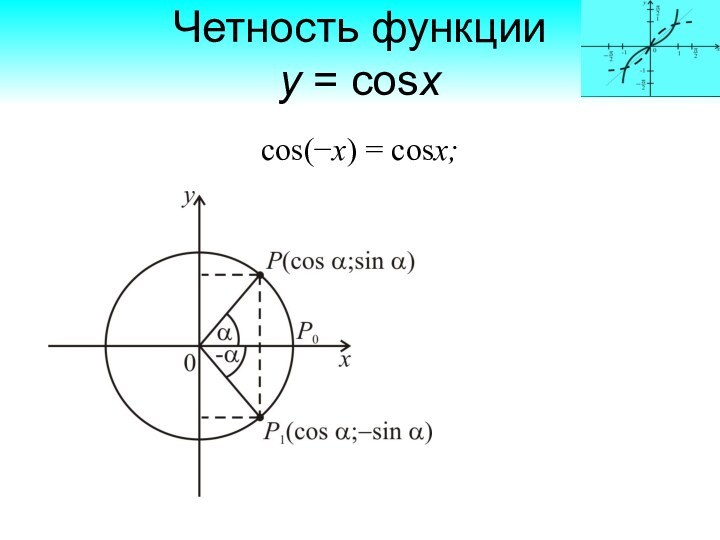
Слайд 10 Четность функции у = cosx
cos(−х) = cosх;

Слайд 11 Периодичность у = cosх
Посмотрим на единичную

окружность и заметим, что cos ( x + 2π)

= cos ( x).
Аналогично cos ( x − 2π) = cos ( x).
О таких функциях говорят, что они периодические с периодом 2π. Если сделать несколько оборотов, например 2π∙n, где n є Z, то значения функции косинуса не изменится:

Слайд 12 cos(x + 2πn) = cos (x). Число 2πn

cos(x + 2πn) = cos (x). Число 2πn также период функции.

также период функции. Число 2π – наименьший положительный период.

Слайд 13 Максимальное и

Максимальное и минимальное значенияФункция у = cosx

минимальное значения
Функция у = cosx принимает максимальное значение,

равное 1. Это в точках х = 2k,
где k .
И минимальное значение,
равное –1, в точках
х =  + 2k, где k .

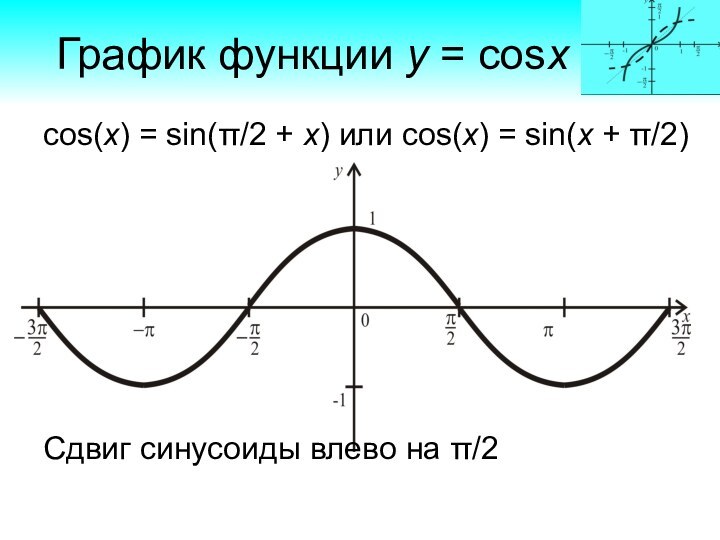
Слайд 14 График функции y = cosx
cos(x) =

sin(2 + x) или cos(x) = sin(x + 2)

Сдвиг синусоиды влево на 2

Слайд 15 Функции тангенс и котангенс
Числовые функции, заданные равенствами у

Функции тангенс и котангенсЧисловые функции, заданные равенствами у = tg x

= tg x и y = ctg x, называются

соответственно тангенсом и котангенсом.
Областью определения тангенса является множество всех чисел х, для которых cos x ≠ 0.
Областью определения котангенса является множество всех чисел х, для которых sin x ≠ 0.

Слайд 16 Множество значений тангенса и котангенса – вся числовая

Множество значений тангенса и котангенса – вся числовая прямая, т.е. R.

прямая, т.е. R.
Тангенс и котангенс являются нечетными функциями
tg(−α)

= − tg α;
ctg(−α) = − ctg α.

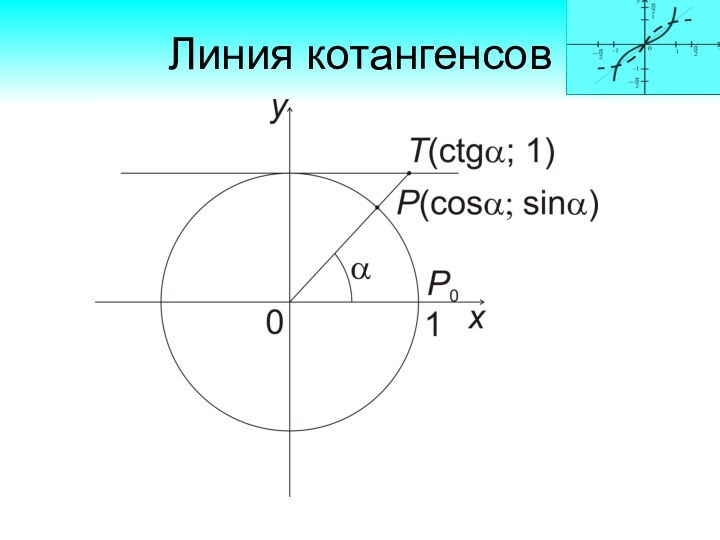
Слайд 17 Линия тангенсов
Прямая ОР проходит через начало координат и

Линия тангенсовПрямая ОР проходит через начало координат и точку Р(cosα ;

точку Р(cosα ; sinα). Ее уравнение y = tg

α∙x.
Абсцисса точки Т, лежащей на этой прямой, равна 1.
Найдем ординату из уравнения прямой.
Получим tg α.

Слайд 18 Вывод
Чтобы найти значение тангенса для конкретного аргумента х,

ВыводЧтобы найти значение тангенса для конкретного аргумента х, надо изобразить линию

надо изобразить линию тангенсов, отложить на единичной окружности аргумент

х, через полученную точку и начало координат провести прямую до пересечения с линией тангенсов, ордината полученной точки будет значением тангенса.

Слайд 19 Табличные значения
tg 0 =

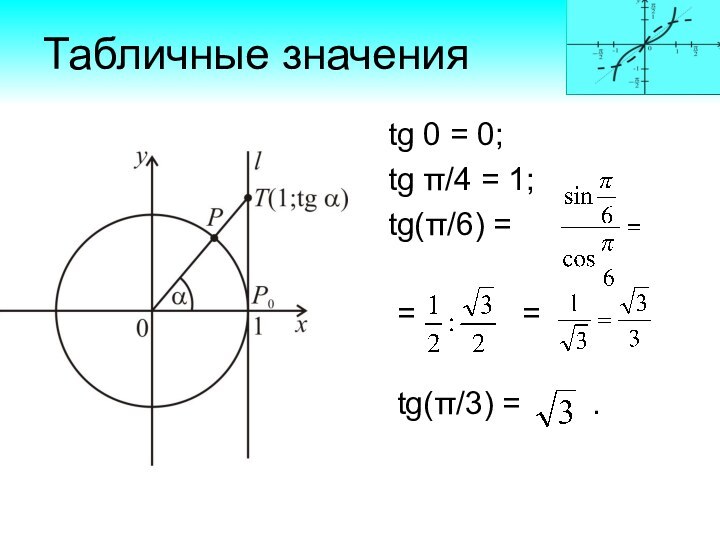
Табличные значения tg 0 = 0; tg  = 1;

0;
tg  = 1;
tg(/6) =

= =

tg(/3) = .

Слайд 20 Табличные значения
tg() = 1;

tg(6) =

;
tg(/3) =  .
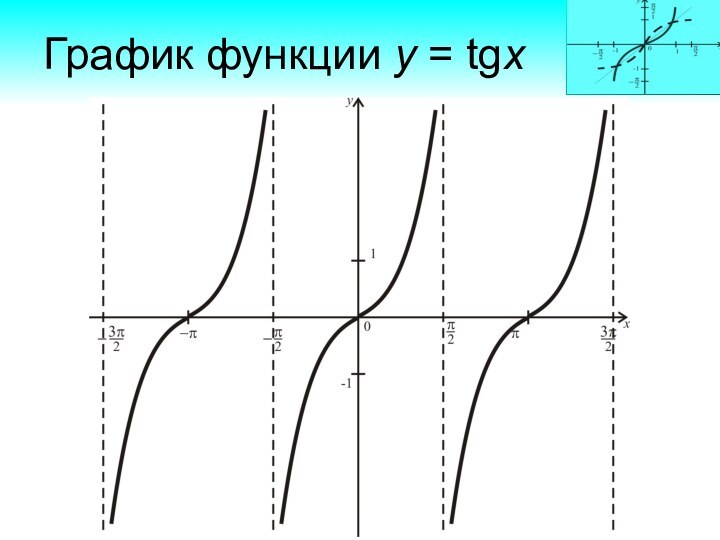
Период функции у = tgx равен k,
где k .
Наименьший положительный период равен  (при k = 1).

Слайд 21 График функции y = tgx

Слайд 22 Линия котангенсов

Слайд 23 Табличные значения
ctg 0 не

Табличные значенияctg 0 не существует. ctg () = 1;

существует.
ctg () = 1;
ctg(/6) =

1/tg (/6) = ;

ctg(/3) = 1/tg(/3) = ;

ctg (2) = 0.

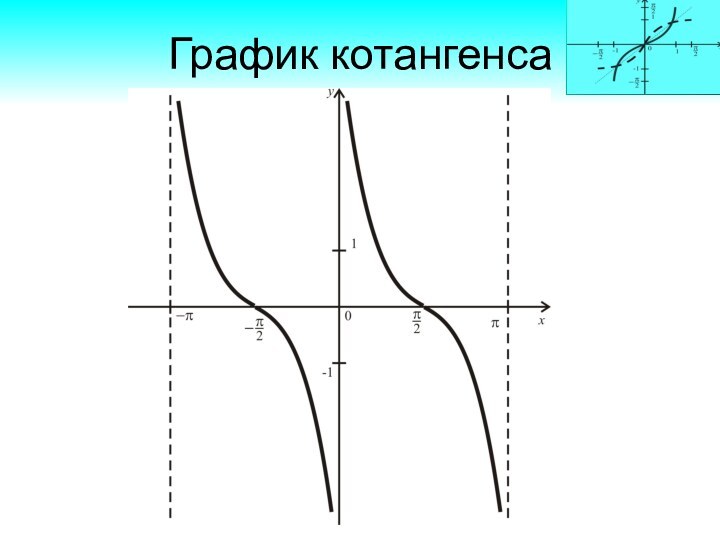
Слайд 24 Период функции y = ctgx
Период функции

равен k, где k  ,
то есть
ctg(x) = ctg(x

+ k), где k  .
Наименьший положительный период равен  (при k = 1).

Слайд 25 График котангенса

Слайд 26 Функции секонс и косеконс
Функция у = 1/cosx называется

секонсом:
y = 1/cosx = secx.
Ее область определения: все

то множество х, где cosx ≠ 0, т.е.
х ≠ π/2 + πk, где k є Z.
Функция y = 1/sinx называется косеконсом: y = 1/sinx = cosecx.
Def(1/sinx) – это то множество х, где
sinx ≠ 0, т.е. х ≠ πn, где n є Z.