Презентация на тему ЦАП и Теорема Котельникова

заслуги перед Отечеством» I степени (21 сентября 2003 года) 
— за выдающиеся достижения

в развитии отечественной науки и многолетнюю
плодотворную деятельность[1]
Орден «За заслуги перед Отечеством» II степени (6 июля 1998 года) —
 за выдающиеся заслуги перед государством, большой личный вклад
в развитие отечественной науки и подготовку
высококвалифицированных кадров[2]
Орден Почёта
Дважды Герой Социалистического Труда (1969, 1978),
6 орденов Ленина,
Орден Октябрьской Революции (5 сентября 1983)
2 ордена Трудового Красного Знамени,
Орден «Знак Почёта»,
Ленинская премия (1964)
2 Сталинские премии (1943, 1946)
Знак отличия «За заслуги перед Москвой» (26 августа 2003) — за большой вклад в развитие отечественной науки и техники, подготовку научных кадров, многолетнюю плодотворную деятельность, способствующую социально-экономическому развитию Москвы[3]
Лауреат Ленинской премии (1964), Сталинской премии (1943, 1946), премии Совета Министров СССР. Награждён Большой золотой медалью имени М. В. Ломоносова АН СССР (1981), золотой медалью имени А. С. Попова АН СССР (1974), золотой медалью имени М. В. Келдыша АН СССР (1987), золотой медалью имени А. Г. Белла (2000).
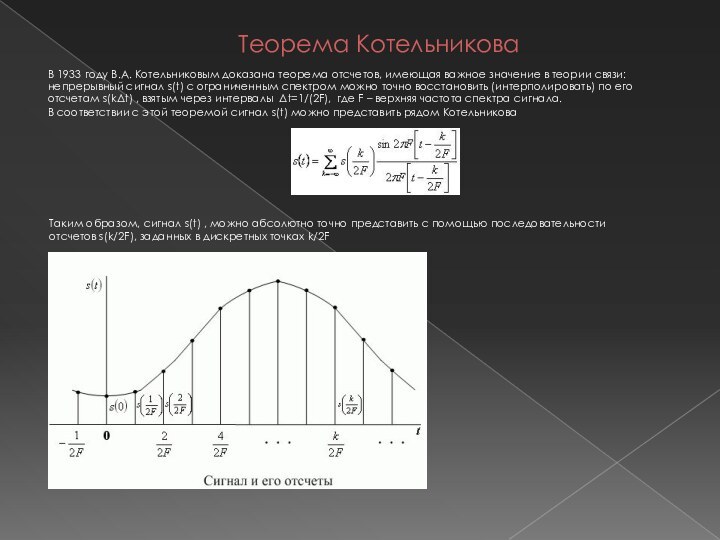
В 1999 г. Международный научный фонд Эдуарда Рейна (Германия) наградил В. А. Котельникова своей основной премией в номинации «за фундаментальные исследования» за впервые математически точно сформулированную и доказанную, в аспекте коммуникационных технологий, теорему отсчетов.
Именем В. А. Котельникова назван астероид № 2726 (в Международном каталоге циркуляр № 9214). Его имя носит военно-морское судно и Институт радиотехники и электроники РАН.

сигнале, в цифровой код.
Цифро-аналоговое преобразование призвано выполнять обратную задачу,

т.е. преобразовывать число, представленное в виде цифрового кода, в эквивалентный аналоговый сигнал.
Цифро-аналоговые преобразователи устанавливаются обычно на выходе микропроцессорной системы для преобразования ее выходных кодов в аналоговый.

Преобразование Бывает:

поэтому параметры ЦАП во многом определяют параметры всей системы

в целом. Далее перечислены наиболее важные характеристики ЦАП.
Разрядность — количество различных уровней выходного сигнала, которые ЦАП может воспроизвести. Обычно задается в битах; количество бит есть логарифм по основанию 2 от количества уровней. Например, однобитный ЦАП способен воспроизвести два (2^1) уровня, а восьмибитный — 256 (2^8) уровней. Разрядность тесно связана с эффективной разрядностью (англ. ENOB — Effective Number of Bits), которая показывает реальное разрешение, достижимое на данном ЦАП.
Максимальная частота дискретизации — максимальная частота, на которой ЦАП может работать, выдавая на выходе корректный результат. В соответствии с теоремой Котельникова, для корректного воспроизведения аналогового сигнала из цифровой формы необходимо, чтобы частота дискретизации была не менее, чем удвоенная максимальная частота в спектре сигнала. Например, для воспроизведения всего слышимого звука, спектр которого простирается до 20 кГц, необходимо, чтобы звуковой сигнал был дискретизован с частотой не менее 40 кГц. Стандарт Audio CD устанавливает частоту дискретизации звукового сигнала 44,1 кГц; для воспроизведения данного сигнала понадобится ЦАП, способный работать на этой частоте. В дешевых компьютерных звуковых картах частота дискретизации составляет 48 кГц. Сигналы, дискретизованные на других частотах, подвергаются передискретизации до 48 кГц, что частично ухудшает качество сигнала.
Монотонность — свойство ЦАП увеличивать аналоговый выходной сигнал при увеличении входного кода.
THD+N (суммарные гармонические искажения + шум) — мера искажений и шума вносимых в сигнал ЦАПом. Выражается в процентах мощности гармоник и шума в выходном сигнале. Важный параметр при малосигнальных применениях ЦАП.
Динамический диапазон — соотношение наибольшего и наименьшего сигналов, которые может воспроизвести ЦАП, выражается в децибелах.

сигнала, полученное при увеличении кода на 1 младший значащий

разряд (МЗР), отличается от правильного значения;
INL (интегральная нелинейность) характеризует, насколько передаточная характеристика ЦАП отличается от идеальной. Идеальная характеристика строго линейна; INL показывает, насколько напряжение на выходе ЦАП при заданном коде отстоит от линейной характеристики; выражается в МЗР;
усиление;
смещение.
Частотные характеристики:
SNDR (отношение сигнал/шум+искажения) характеризует в децибелах отношение мощности выходного сигнала к суммарной мощности шума и гармонических искажений;
HDi (коэффициент i-й гармоники) характеризует отношение i-й гармоники к основной гармонике;
THD (коэффициент гармонических искажений) — отношение суммарной мощности всех гармоник (кроме первой) к мощности первой гармоники.

цепи соответственно Iin/2, Iin/4, Iin/8 и т.д. Для преобразования входного цифрового кода

в выходной ток достаточно собрать все токи плечей, соответствующих единицам во входном коде, в выходной точке преобразователя.

Если к выходной точке преобразователя подключить операционный усилитель, то выходное напряжение можно определить как:

где K – входной цифровой код, N – разрядность ЦАП.

 Все существующие ЦАП делятся на две больших группы: ЦАП с выходом по току и ЦАП с выходом по напряжению. Различие между ними заключается в отсутствии или наличии у микросхемы ЦАП оконечного каскада на операционном усилителе. ЦАП с выходом по напряжению являются более завершенными устройствами и требуют меньше дополнительных элементов для своей работы. Однако, оконечный каскад наряду с параметрами лесничной схемы определяет динамические и точностные параметры ЦАП. Выполнить точный быстродействующий операционный усилитель на одном кристалле с ЦАП часто бывает затруднительно. Поэтому большинство быстродействующих ЦАП имеют выход по току.

отсчетов, имеющая важное значение в теории связи: непрерывный сигнал s(t)

с ограниченным спектром можно точно восстановить (интерполировать) по его отсчетам s(kΔt) , взятым через интервалы  Δt=1/(2F), где F – верхняя частота спектра сигнала.
В соответствии с этой теоремой сигнал s(t) можно представить рядом Котельникова

Таким образом, сигнал s(t) , можно абсолютно точно представить с помощью последовательности отсчетов s(k/2F), заданных в дискретных точках k/2F

в пределах которого сосредоточена основная часть его энергии и

которым определяется ширина спектра сигнала. В ряде случаев спектр сознательно сокращают. Это обусловлено тем, что аппаратура и линия связи должны иметь минимальную полосу частот. Сокращение спектра выполняют, исходя из допустимых искажений сигнала. Например, при телефонной связи хорошая разборчивость речи и узнаваемость абонента обеспечиваются при передаче сигналов в полосе частот ΔF = 0.3…3.4 кГц.
Увеличение  ΔF приводит к неоправданному усложнению аппаратуры и повышению затрат. Для передачи телевизионного изображения при стандарте в 625 строк полоса частот, занимаемая сигналом, составляет около 6 МГц.

Из вышесказанного следует, что процессы с ограниченными спектрами могут служить адекватными математическими моделями многих реальных сигналов.

Функция вида: называется функцией отсчетов.


Она характеризуется следующими свойствами. Если k=0, функция отсчетов имеет максимальное значение при t=0 , а в моменты времени t=i/2f (i=1,2,3….) она обращается в нуль; ширина главного лепестка функции отсчетов на нулевом уровне равна 1/F, поэтому минимальная длительность импульса, который может существовать на выходе линейной системы с полосой пропускания F, равна 1/F; функции отсчетов ортогональны на бесконечном интервале времени.