- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Управление рисками
Содержание
- 2. ВариацияВариацией (variatio — изменение, перемена) называется изменение или отклонение
- 3. Показатели вариацииАбсолютные показателиразмах вариациисреднее линейное отклонениедисперсиясреднеквадратическое отклонениестандартное отклонениеОтносительные показателиотносительный размах вариации линейный коэффициент вариациикоэффициент вариации
- 4. Размах вариацииРазмах вариации — это разность между максимальным
- 5. Среднее линейное отклонениеЭто средняя арифметическая из абсолютных отклонений
- 6. ДисперсияДисперсия (2)- представляет собой средний квадрат отклонений индивидуальных
- 7. Среднеквадратическое отклонениеСреднее квадратическое отклонение () равно квадратному корню
- 8. Правило трёх сигмПравило трёх сигм (3) — практически все
- 9. Стандартное отклонениеСтандартное отклонение - оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии:
- 10. Относительный размах вариации Относительный размах вариации (коэффициент осцилляции) определяется формулой:
- 11. Линейный коэффициент вариацииОтносительное линейное отклонение определяется формулой:
- 12. Коэффициент вариацииКоэффициент вариации определяется формулой:
- 13. Пример расчета показателей вариацииНа этапе отбора кандидатов
- 15. Вычислим средний производственный опыт работы, летРассчитаем дисперсию
- 16. Задача 1Известно, что месячный финансовый результат торговой
- 17. Задача 2В предыдущие 100 дней финансовый результат
- 18. Задача 2 (решение)средняя ожидаемая доходность: 92 (100)
- 19. Скачать презентацию
- 20. Похожие презентации
ВариацияВариацией (variatio — изменение, перемена) называется изменение или отклонение какого-либо показателя.Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности.
















Слайд 2
Вариация
Вариацией (variatio — изменение, перемена) называется изменение или отклонение какого-либо
показателя.
совокупности.
Слайд 3
Показатели вариации
Абсолютные показатели
размах вариации
среднее линейное отклонение
дисперсия
среднеквадратическое отклонение
стандартное отклонение
Относительные
показатели
относительный размах вариации
линейный коэффициент вариации
коэффициент вариации
Слайд 4
Размах вариации
Размах вариации — это разность между максимальным и
минимальным значениями признака.
Пример: Опыт работы у пяти претендентов на
предшествующей работе составляет: 2,3,4,7 и 9 лет.
Решение: размах вариации = 9 — 2 = 7 лет.
Слайд 5
Среднее линейное отклонение
Это средняя арифметическая из абсолютных отклонений отдельных
значений признака от средней
Где — среднее арифметическое значений выборки
Пример:
Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.В нашем примере: лет;
Слайд 6
Дисперсия
Дисперсия (2)- представляет собой средний квадрат отклонений индивидуальных значений
признака от их средней величины.
В нашем примере: 2 =
6,8Более удобно вычислять дисперсию по формуле:
которая получается из основной путем преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Слайд 7
Среднеквадратическое отклонение
Среднее квадратическое отклонение () равно квадратному корню из
среднего квадрата отклонений отдельных значений признака от средней арифметической.
В общем
смысле среднеквадратическое отклонение можно считать мерой неопределённости.В Теории управлением капиталом среднее квадратическое отклонение доходности портфеля отождествляется с риском портфеля.
Слайд 8
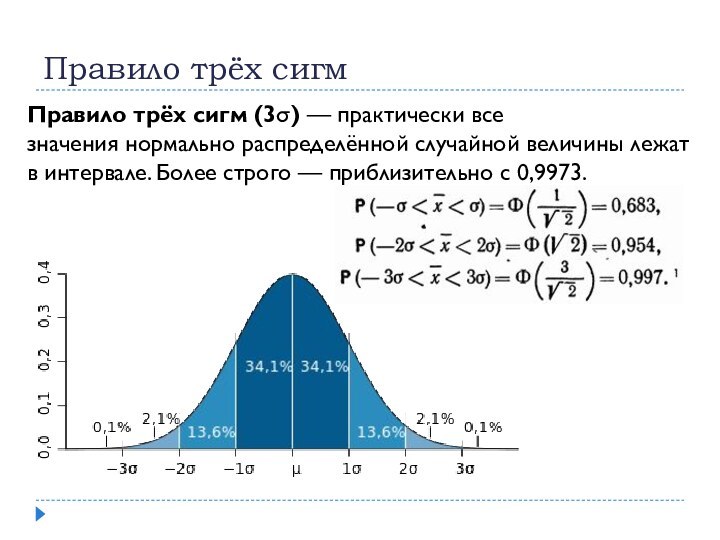
Правило трёх сигм
Правило трёх сигм (3) — практически все значения нормально
распределённой случайной величины лежат в интервале. Более строго — приблизительно с
0,9973.
Слайд 9
Стандартное отклонение
Стандартное отклонение - оценка среднеквадратического отклонения случайной величины x относительно
её математического ожидания на основе несмещённой оценки её дисперсии:
Слайд 10
Относительный размах вариации
Относительный размах вариации (коэффициент осцилляции)
определяется формулой:
Слайд 13
Пример расчета показателей вариации
На этапе отбора кандидатов для
участия в осуществлении сложного проекта фирма объявила конкурс профессионалов.
Распределение претендентов по опыту работы показало следующие результаты:Опыт работы до 4 лет – 10 чел.
Опыт работы от 4 – до 6 лет – 10 чел.
Опыт работы от 6 – до 8 лет – 50 чел.
Опыт работы от 8 – до 10 лет – 20 чел.
Опыт работы от 10 лет – 10 чел.
Слайд 15
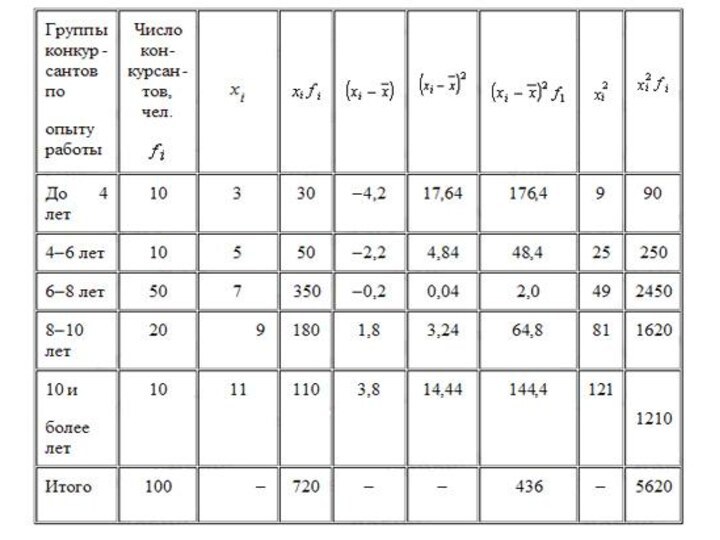
Вычислим средний производственный опыт работы, лет
Рассчитаем дисперсию по
продолжительности опыта работы
Такой же результат получается, если использовать для
расчета другую формулу расчета дисперсииВычислим среднее квадратическое отклонение, лет:
Определим коэффициент вариации, %:
Слайд 16
Задача 1
Известно, что месячный финансовый результат торговой организации
в предыдущий год был следующим:
Рассчитать основные статистические показатели распределения
месячного финансового результата торговой организации.
Слайд 17
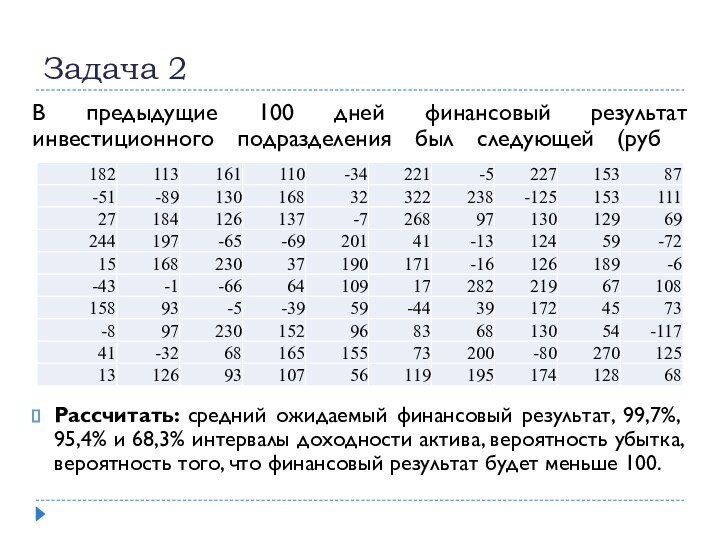
Задача 2
В предыдущие 100 дней финансовый результат инвестиционного
подразделения был следующей (руб.):
НОРМОБР(СЛЧИС();100;100)Рассчитать: средний ожидаемый финансовый результат, 99,7%, 95,4% и 68,3% интервалы доходности актива, вероятность убытка, вероятность того, что финансовый результат будет меньше 100.
Слайд 18
Задача 2 (решение)
средняя ожидаемая доходность: 92 (100)
=СРЗНАЧ(F16:O25)
интервал
99,7%: от -199 до 383
интервал 95,4%: от
-102 до 285интервал 68,3%: от -5 до 189
вероятность убытка: 17%
=НОРМ.РАСП(0;$E$33;$E$32;ИСТИНА)
вероятность меньше 100 : 53%
=НОРМ.РАСП(100;$E$33;$E$32;ИСТИНА)





























