- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задача № 2
Содержание
- 2. УсловиеНайти все значения параметра а, при которых
- 3. УсловиеДля удобства перепишем условие задачи в виде:Теперь
- 4. РешениеПерепишем полученное неравенство в виде: построим график правой части неравенства.
- 5. РешениеДля этого раскроем модуль правой части в
- 6. РешениеНайдем координаты вершин парабол, задаваемых полученными уравнениями
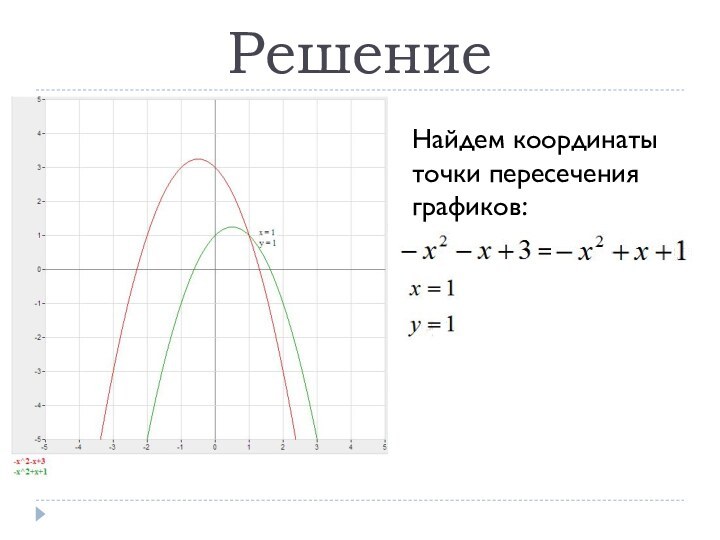
- 7. РешениеНайдем координаты точки пересечения графиков:
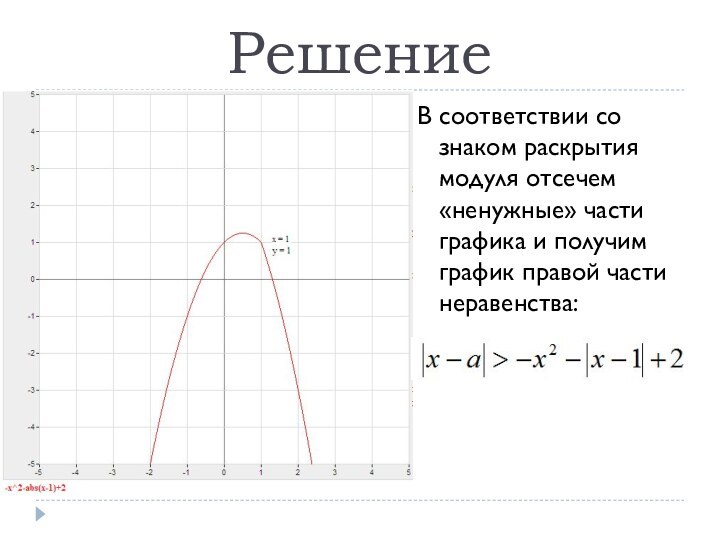
- 8. РешениеВ соответствии со знаком раскрытия модуля отсечем «ненужные» части графика и получим график правой части неравенства:
- 9. РешениеТеперь на полученном графике построим график левой
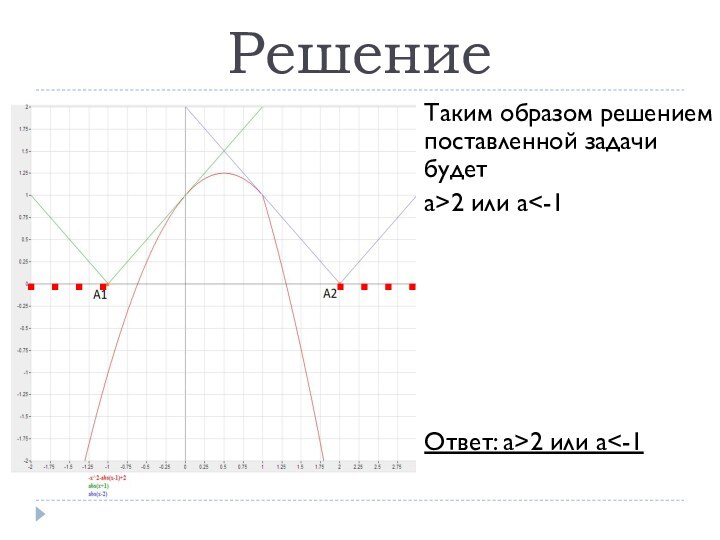
- 10. РешениеДля выполнения этого условия вершина уголка не должна лежать на отрезке [A1;A2].
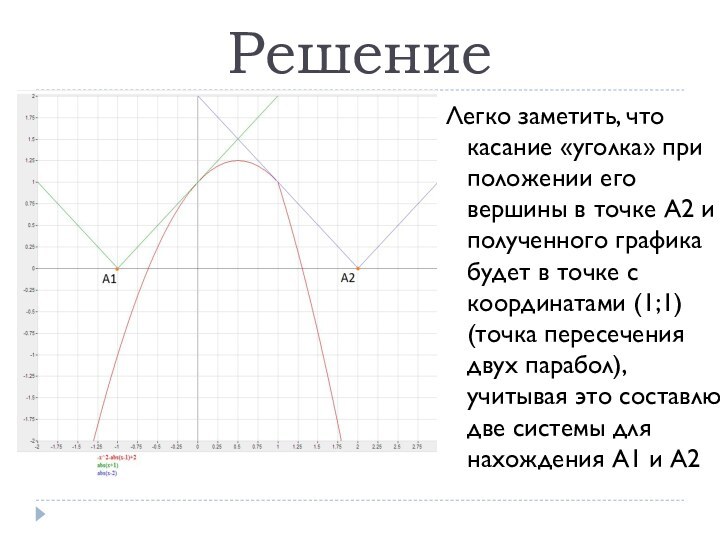
- 11. РешениеЛегко заметить, что касание «уголка» при положении
- 12. РешениеМодуль раскрыт в зависимости от знака угловогокоэффициента
- 13. Скачать презентацию
- 14. Похожие презентации
УсловиеНайти все значения параметра а, при которых наименьшее значение функции больше 2.







![Задача № 2 РешениеДля выполнения этого условия вершина уголка не должна лежать на отрезке [A1;A2].](/img/tmb/14/1387739/e54d2ab4cbc2938cdb8cb6697fbd4169-720x.jpg)

Слайд 3
Условие
Для удобства перепишем условие задачи в виде:
Теперь нам
нужно найти такое значение параметра, чтобы данное неравенство выполнялось
при всех значениях X.
Слайд 6
Решение
Найдем координаты вершин парабол, задаваемых полученными уравнениями и
построим их на координатной плоскости:
x0 =-0,5
x0 =0,5y0=3,25 y0=1,25
Слайд 8
Решение
В соответствии со знаком раскрытия модуля отсечем «ненужные»
части графика и получим график правой части неравенства:
Слайд 9
Решение
Теперь на полученном графике построим график левой части
неравенства, он будет представлять собой так называемый «уголок», который
в зависимости от значения параметра a будет перемещаться вдоль оси абсцисс.Нам нужно, чтобы этот «уголок» располагался так, чтобы на графике правой части неравенства не нашлось ни одной точки, лежащей выше соответственных точек «уголка» или даже на самом «уголке» (строгое неравенство).





























