Презентация на тему Звездчатые многогранники

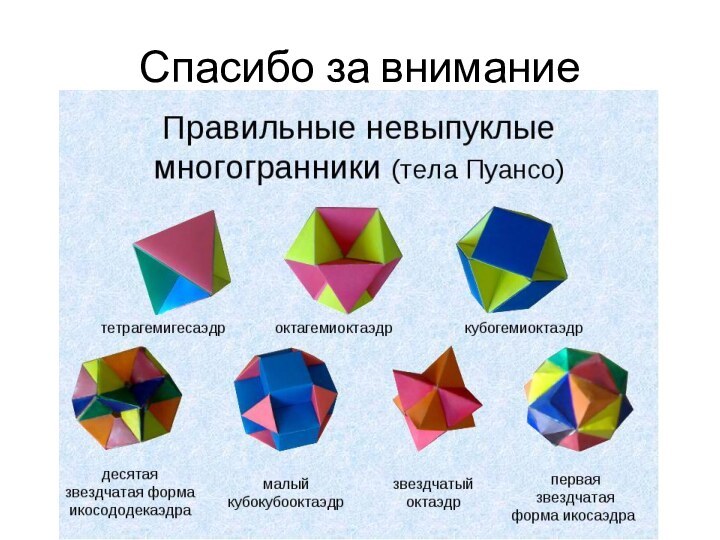
между собой. Как и у незвёздчатых многогранников, грани попарно

соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами).
Представители необъёмных видов геометрических тел, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.

(поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней),

ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.

граней данного многогранника через рёбра до их следующего пересечения

с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники — это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. В отличие от пяти классических правильных многогранников , данные многогранники не являются выпуклыми телами.Существует ровно 4 тел такого вида.

являются правильные или звёздчатые многоугольники, но не обязательно одинаковые.

При этом строение всех вершин должно быть одинаковым (условие однородности). Существует 53 различных ПЗМ.
Однородные многогранники — правильные и полуправильные выпуклые многогранники ; правильные и полуправильные звёздчатые многогранники вместе называются однородными многогранниками. У этих тел все грани являются правильными многоугольниками (выпуклыми или звёздчатыми), а все вершины одинаковы (то есть существуют ортогональные преобразования многогранника в себя, переводящие любую вершину в любую другую). Существует ровно 75 однородных многогранников.

понимается процесс построения многогранника из другого многогранника путём расширения

его граней. Для этого через грани исходного многогранника проводятся плоскости и рассматриваются всевозможные рёбра, полученные в результате пересечения этих плоскостей, и выбираются подходящие
Куб и тетраэдр не позволяют приведение к звёздчатой форме. Октаэдр имеет единственное построение — звёздчатый октаэдр. Додекаэдр даёт три звёздчатые формы

одну
Додекаэдр имеет три
Икосаэдр имеет 59, из которых 32 обладают

полной, а 27 — неполной икосаэдральной симметрией.Существует Большой икосаэдр
Кубооктаэдр имеет 4
Икосододекаэдр имеет множество форм.