Презентация на тему урока алгебры в 9 классе по теме Функции и графики. Итоговое повторение.

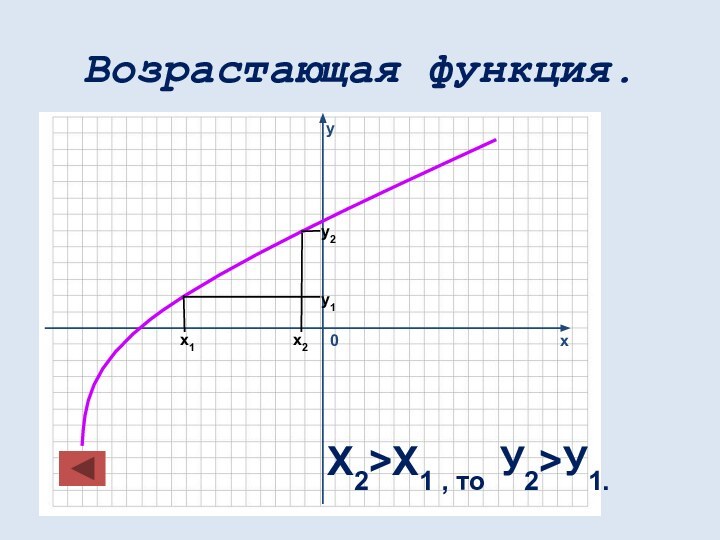
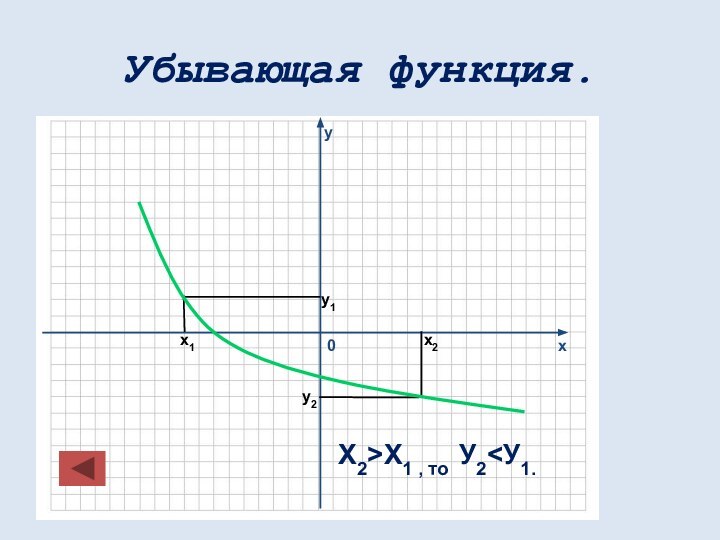
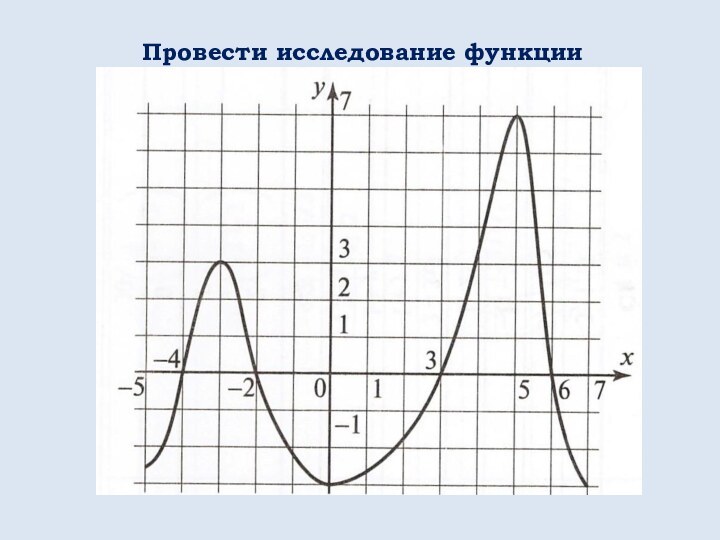
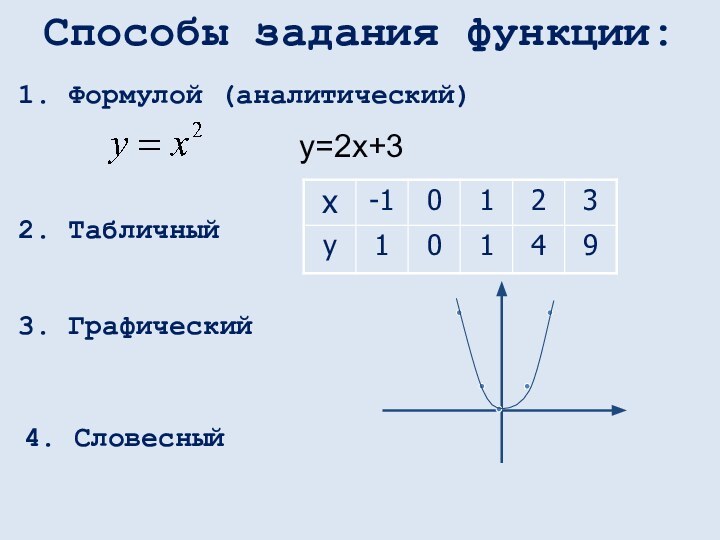
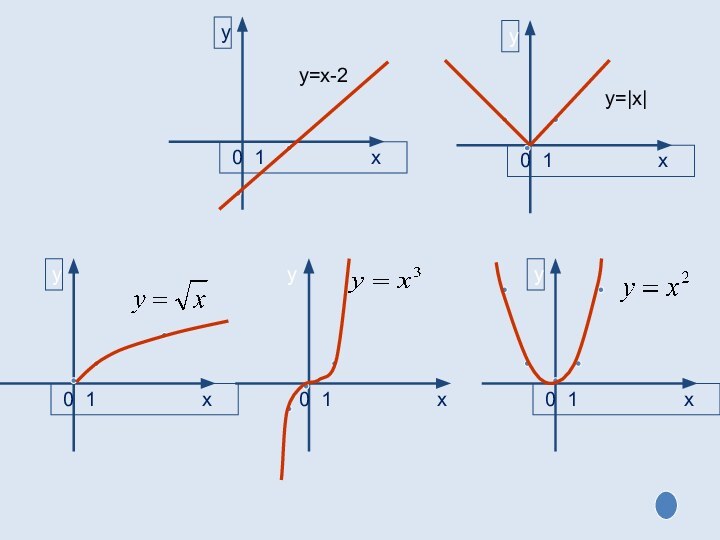
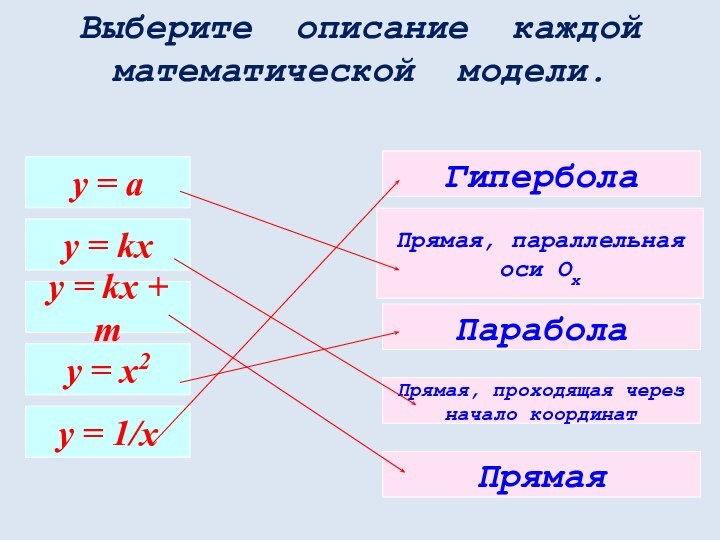
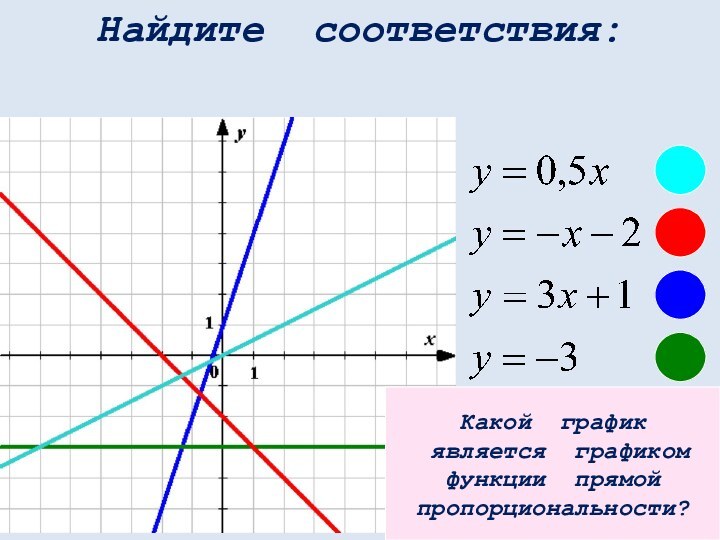
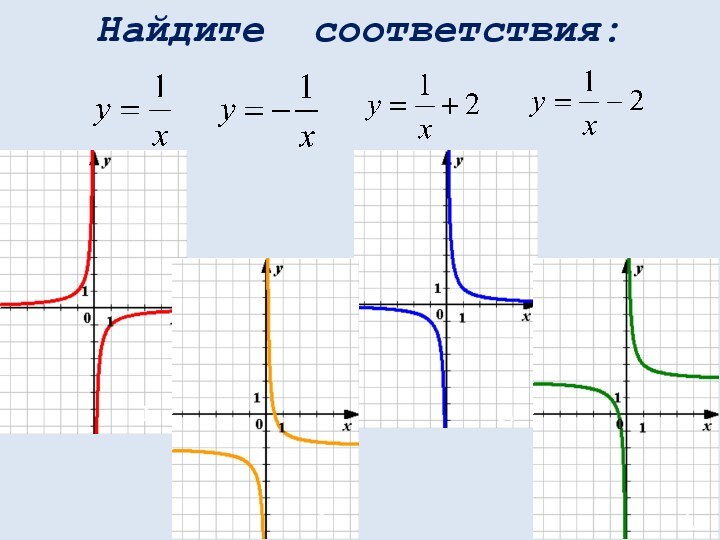
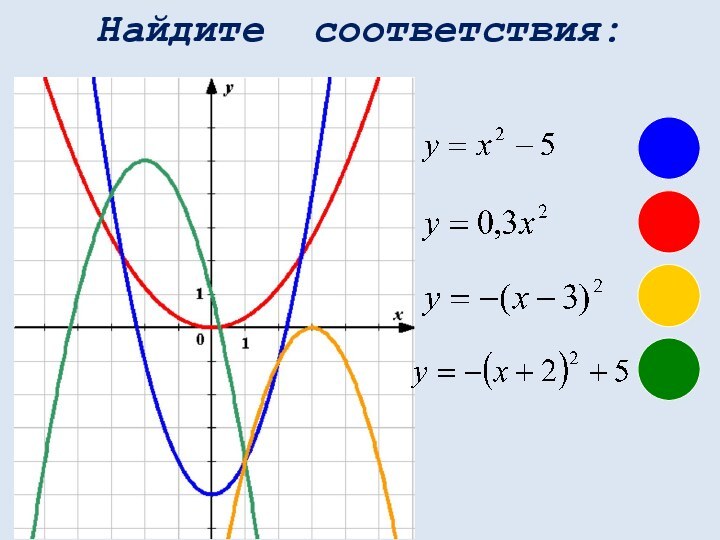
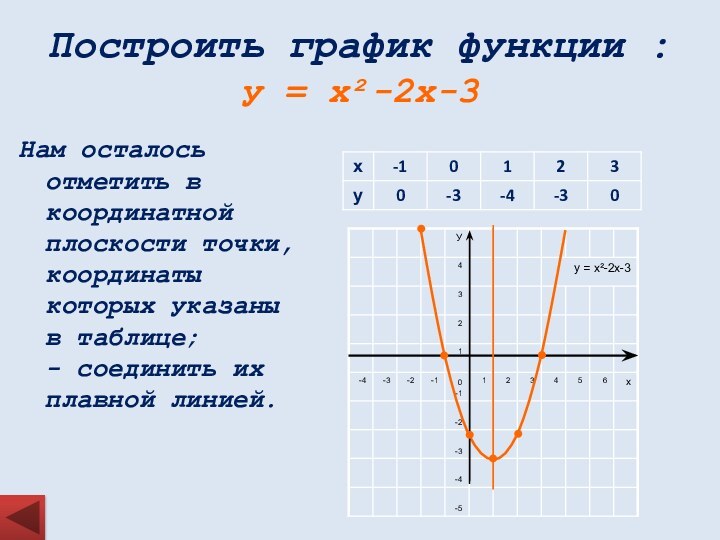
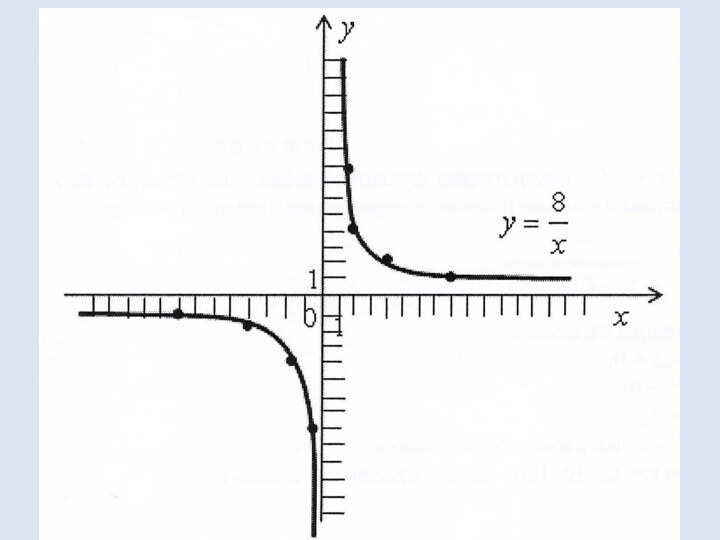
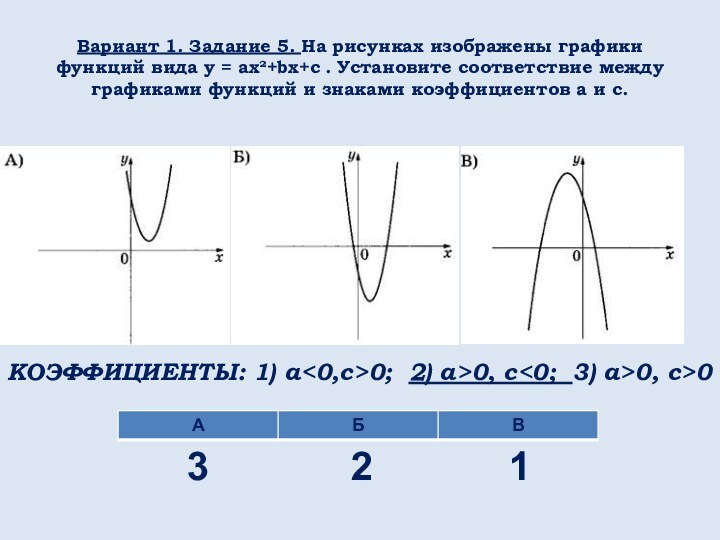
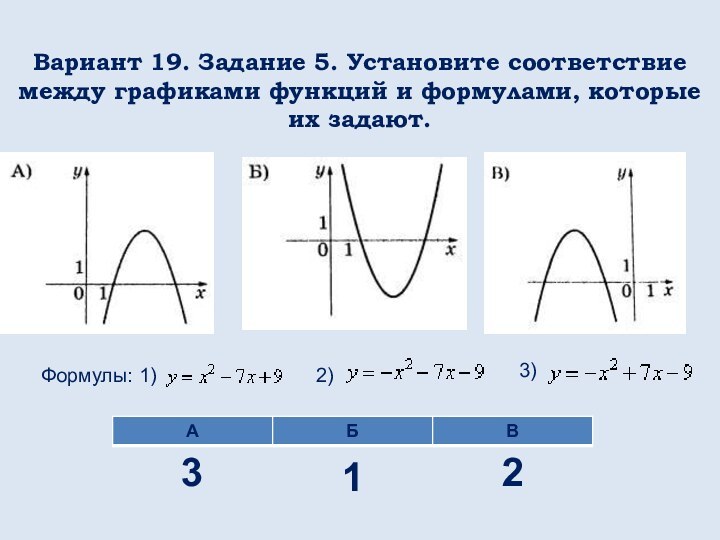
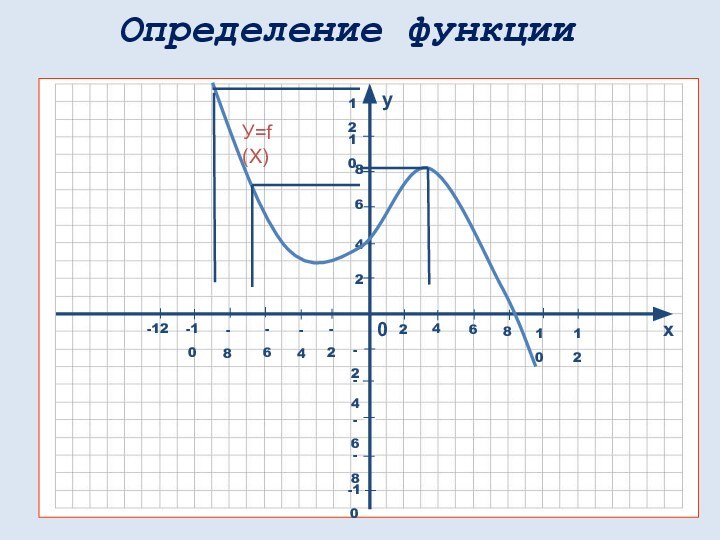
математических понятий, выражающее зависимость между переменными величинами.
Слово «функция» (от

Как термин «функция от x» стало употребляться впервые в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли

Готфрид Вильгельм фон Лейбниц

Дании́л Берну́лли

– 1783), вводя понятие функции, говорил, что «когда некоторые

В формировании современного понимания функциональной зависимости приняли участие многие крупные математики. Описание функции, почти совпадающее с современным, встречается уже в учебниках математики начала XIX в. Активным сторонником такого понимания функции был Н.И. Лобачевский.

леонард эйлер

Николай Иванович Лобачевский (1792-1856)

она научилась
описывать процессы, движение,
так она стала необходима всем».

не летает

Бездонную бочку водой не наполнишь
Близок локоть, да не

Пословицы и поговорки с точки зрения функциональной зависимости

того много и спрашивается
Каков строитель, такова и обитель
К чему

Меньше говори, больше делай

Работает – как ребенок, а ест – как детина
В умной беседе ума набраться, а в глупой свой растерять
Худой мир лучше доброй войны
Тише едешь – дальше будешь
Не все то золото, что блестит

Прямая зависимость

Обратная зависимость

значений, которые может принимать ее аргумент (х) D(х)





Все действительные

Все действительные числа

Х+1≠0 ⇒ Х≠-1

2х-6≥0 ⇒ 2х≥6 ⇒ х≥3 или│3;+∞)

называют множество всех значений которые может принимать переменная у

Все действительные числа

у≥0

у≠0

у≥0

знакопостоянства
У>0 при X∈ (-3; 7);
У

У=0 при X=-3 и X=7

+ m
y = x2
y = 1/x
Прямая, параллельная
оси Ох
Парабола
Гипербола
Прямая,

Прямая

Выберите описание каждой
математической модели.

bх +с.
1.
Определить направление ветвей параболы.
2.
Провести ось симметрии.
3.
4.
Определить точки пересечения

5.

Составить таблицу значений функции
с учетом оси симметрии параболы. (Найти дополнительные точки)

Найти координаты вершины параболы
(m; n).

Найти точки пересечения графика функции с осью Оу, подставив в y = ax2+bx+c х=0

6.

= х²-2х-3 – квадратичная функция, графиком является парабола.
1. Ветви

осталось отметить в координатной плоскости точки, координаты которых указаны

график обратной пропорциональности, к>0 – ветви графика расположены в

2.Составим таблицу значений для х>0

3.Вторую ветвь получаем «отражением» относительно начала координат

под ред.
И. В. Ященко. — М. : Издательство

функций вида y = ax²+bx+c . Установите соответствие между

КОЭФФИЦИЕНТЫ: 1) a<0,c>0; 2) a>0, c<0; 3) a>0, c>0

3

2

1

и их графиками.
ФУНКЦИИ: А) y = -3x;

1

2

3

функций вида y = kx + b. Установите соответствие

КОЭФФИЦИЕНТЫ: 1) k>0, b<0; 2) k<0, b<0; 3) k>0, b>0

2

3

1

и их графиками.
Функции: А)
Б)
В)
3
1
2
А)
т
= -(-7:2) =3,5
В)
т
= -(7:2)

функций и формулами, которые их задают.
Формулы: 1)
2)
3)
1
3
2