П. Д. Коэн
План.
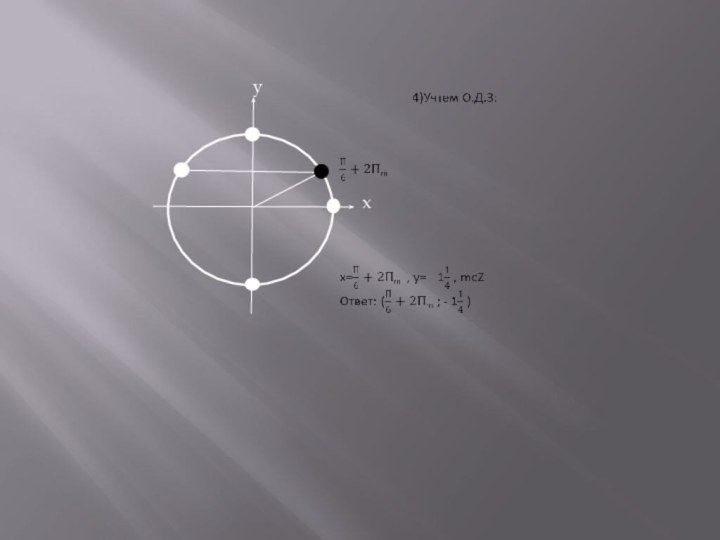
1.Решение системы уравнений, содержащей логарифм.
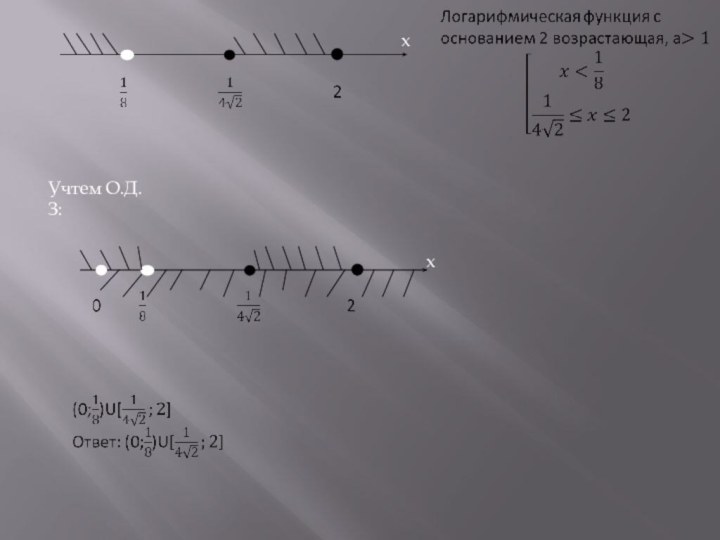
2.Решение неравенства, содержащего логарифм.
3.Решение геометрической задачи.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





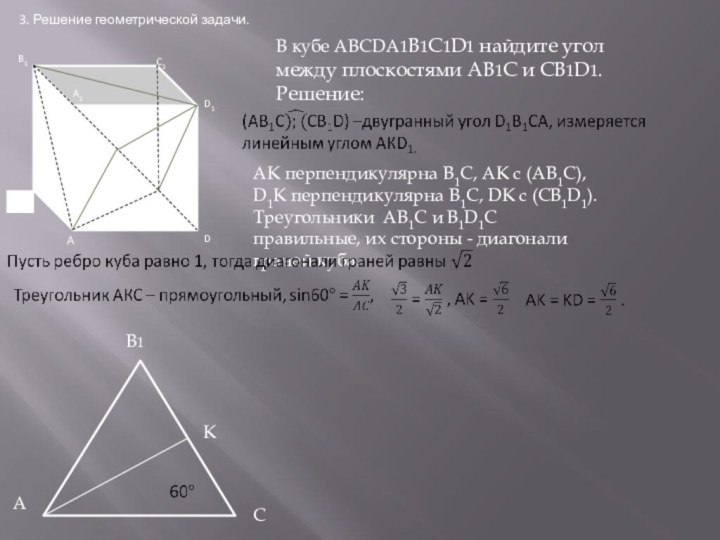



В1
К
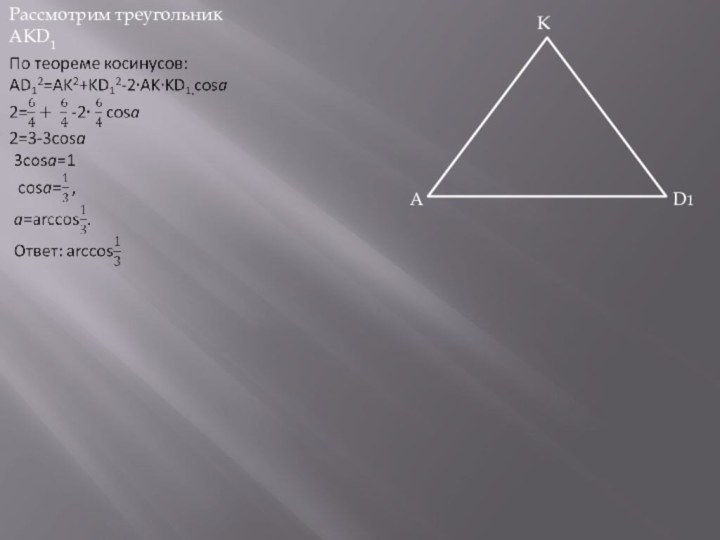
А
С
А
В
С
D
A1
B1
C1
D1
K
M
P
H
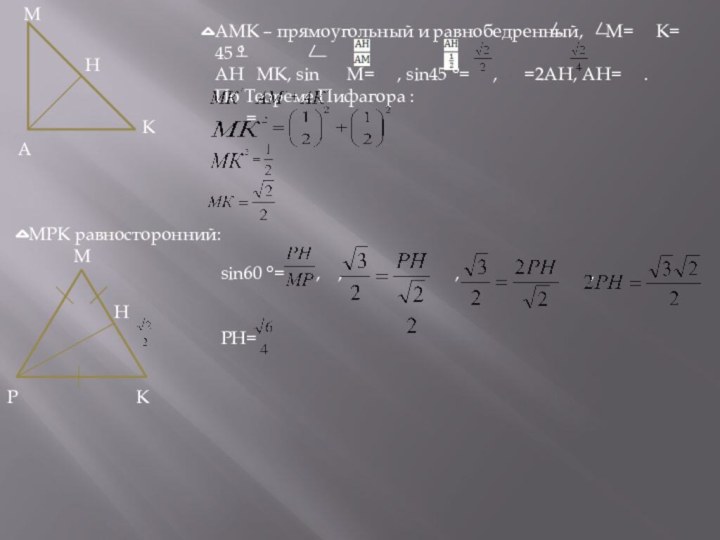
Решение: Грань ВВ1С1С параллельна и равна грани АА1D1D, поэтому угол между ВСС1В1 и (МРК) равен углу между АА1D1D и (МРК). РМКА – двугранный угол, измеряется величиной его линейного угла. АН МК, АН с (АА1D)
РН МК, РН с (КМР).
АНР – линейный. У куба все ребра равны. Пусть ребро куба 1, тогда АК=АМ=АР=
МРК равносторонний:
М
Р
К
Н
sin60 °= , , , ,
РН=